Children notice shapes from a young age, even if they don’t know what the shapes are called. Young kids usually take longer learning about specific properties of shapes, like how many sides each shape has or how it looks. By practicing with shapes frequently, preschoolers will increase their ability to comprehend two-dimensional structures. These children benefit from a knowledge of shapes when studying advanced mathematics.
Numbers are typically the first thing that comes to mind when we think of early mathematical education. There is also another fascinating area of mathematics to be explored and enjoyed, and that is the area of shape! A shape can be described as a geometric figure. It is possible to classify shapes by describing a bigger category of shapes that the shape belongs to. Their different dimensions, for example, can be used to classify them. Thus, circles are two-dimensional shapes that can fit into a flat plane like other 2D shapes.
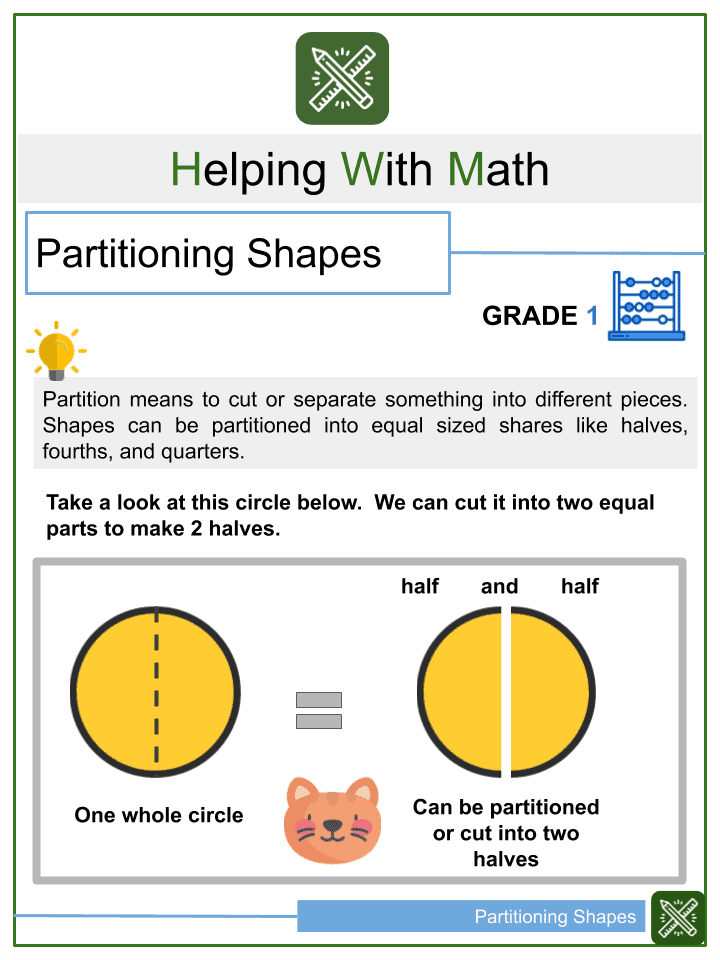
2D Shapes
In geometry, the term 2D (two-dimensional) refers to a flat plane figure or shape with only two dimensions – length and width, without depth or thickness. An example is a piece of paper, which has a two-dimensional shape. The object here consists of a length and width but has neither depth nor height. So, it can be said that a 2-D shape does not have any thickness and can be measured in only two faces. Squares, rectangles, triangles, circles, quadrilaterals, and hexagons are some common 2D shapes. Compared to these, a 3D shape (three-dimensional) has three dimensions – length, width, and height. Dice, for instance, is three-dimensional because it has a length, a width, and a height. Cuboids, cones, pyramids, and cylinders are examples of 3D shapes. Shapes usually have their own patterns and properties. These shapes can vary according to many factors, including the angle, sides, length, width, area, and volume.
2D Shapes with at least three straight sides are known as polygons. They consist of straight-line segments that are connected in order to form a closed shape. A 2-D figure consists of sides, vertices (corners), and internal angles, except for a circle, which is curved. The following figure illustrates some of the most common 2D shapes we encounter.
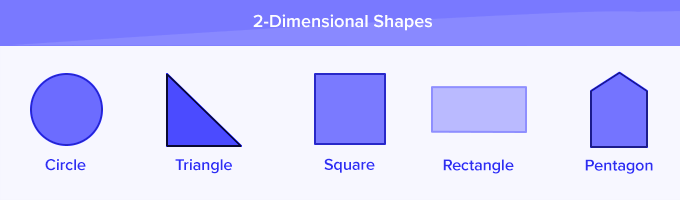
Sides, Vertices and Angles
Lines and corners are the basic building blocks of 2D shapes. These parts of a shape have some special names.
Parts of a 2-D shape
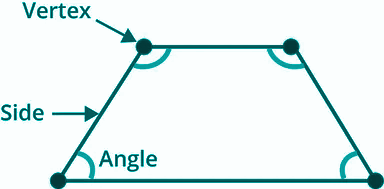
The line segments that make a 2D shape are called its sides.
A corner at which two sides of a 2D shape meet is called a vertex. Two or more corners are called vertices (not vertexes!).
A measure of the turn between the two sides that meets at a vertex is called the angle between the sides.
In this article, we will learn more about 2D shapes.
Its Significance
For future math learning, it is essential to learn 2D shapes. It is one of the first things children learn about shapes. Children as young as 2 can recognize simple 2D shapes, such as circles, and can draw them. If students are unable to recognize 2D shapes, they will not be able to recognize 3D shapes as well, and therefore will not be able to handle geometry. Having a good grasp of 2D shapes is also crucial for determining measurements, as students who fail to recognize a rectangle cannot correctly measure it. Additionally, the shapes aid students in learning words like “side,” “corner,” “angle,” “vertex,” “straight,” and “line.”
Its Benefits
Besides being fundamental to math learning, 2D shapes are critical to life skills and art. Shapes are the foundation of many early drawing and painting lessons. They can also serve as a handy way for non-artists to draw things like stick figures (circles and lines) and houses (a triangle atop a square). When students fill out forms or take standardized tests, they are required to “check the box” or “complete the circle”. These tasks will be difficult for students who are unable to associate 2D shapes with their written names.
Its Features
As already mentioned, 2D shapes are those in which height and width are the only dimensions; there is no depth. 2D shape names are most often associated with pictures in books or shapes drawn on pages, though very flat objects like signs can also be described by them. Objects such as blocks or books have depth in addition to height and width, making them 3D shapes.
Its Identification
Students must see examples of shapes in order to identify them. To ensure that they understand the outlines of the shapes, just show them simple pictures or provide the name of each shape underneath them. If students need assistance, teachers or parents should explain to them the characteristics of each shape, such as how many sides it has, how many corners, whether the lines are straight or curved, and if all the sides are the same. To begin, students should learn the easiest shapes to distinguish, such as circles, triangles, and squares. Next, they can explore rectangles, ovals, and pentagons. Also include hexagons, octagons, parallelograms, and other 2D polygons listed in your school syllabus.
Learning Activities
To reinforce students’ understanding of 2D shapes, they must complete essential activities that help them grasp the subject better. One way is to search for 2D shapes in their surroundings, using them to draw, sort, and categorize them, invent patterns with them, and arrange 2D shapes of different sizes, angles, or colors, such as a small right triangle with a large one.
Talking about 2D shapes
We can use the terms sides and angles to describe any 2D shape. The angle of a 2D shape, if more than one may also be called a ‘vertex’ – or ‘vertices’.
Angles are measured in degrees. An example is 30˚.
Here is a list of 2-D shapes and their properties. Understanding the properties of 2D shapes is a basic but important skill. Properties of shapes may differ depending on whether or not they are equilateral. We have below outlined the properties of the various 2D shapes.
Square
- 4 equal sides
- 4 equal angles (90°)
- 4 axes of symmetry
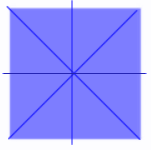
Rectangle
- 2 sets of 2 equal sides
- 4 equal angles (90°)
- 2 axes of symmetry

Circle
- Fixed diameter and radius
- An almost infinite number of axes run through its center

Triangle
- Can have no, 2 or 3 equal sides
- Can have no, 2 or 3 equal angles
- There can be up to 3 axes of symmetry

Pentagon
- Has 5 sides (can be equal)
- Has 5 angles (can be equal)
- Can have as many as 5 axes of symmetry
Hexagon
- With 6 sides (can be equal)
- With 6 angles (can be equal)
- Can have up to 6 axes of symmetry
Octagon
- Has 8 sides (can be equal)
- Has 8 angles (can be equal)
- Having up to 8 axes of symmetry
Parallelogram
- 2 sets of 2 equal sides
- 2 sets of 2 equal angles
- Usually no axes of symmetry

- All sides are of the same length
- 2 sets of 2 equal angles
- There are 2 lines of symmetry
Trapezium
- At least 2 parallel sides
- There can be pairs of equal angles
- Can have a line of symmetry

Regular and Irregular 2D Shapes
According to the length and the interior angles, a 2D shape is considered regular or irregular:
If all the sides of a 2D shape are equal in length and all the angles within it measure the same, it is said to be regular.
An irregular shape is one whose sides are all of unequal length and whose angles are all of unequal size.
The following figure illustrates the difference between regular and irregular 2D shapes.
Regular Irregular

Quadrilateral

Triangle

Pentagon

Hexagon
Reference: https://www.twinkl.co.in/resource/t-n-4529-new-regular-and-irregular-shapes-2d-large-display-poster
Area and Perimeter of 2D Shapes
A 2D shape’s area is the size of the region it encloses. A 2D shape’s perimeter is equal to the sum of its sides. This table summarizes the common formulas for determining an object’s area and perimeter based on a 2D shape:
| 2D Shape | Area Formula | Perimeter Formula |
| Circle | A = π × r2 where ‘π’ is a constant whose value is taken as 22/7 or 3.14 and ‘r’ is the radius of the circle | Circumference (Perimeter) = 2πr |
| Triangle | Area = ½ (Base × Height) | Perimeter = Sum of all three sides |
| Square | Area = Side2 | Perimeter = 4 × side |
| Rectangle | Area = Length × Width | Perimeter = 2 (Length + Width) |
Important Notes
The following are some important points to remember when studying 2D shapes.
A 2D shape can be measured by its width and length.
All the 2D shapes are entirely flat.
All sides and internal angles of a polygon must measure the same to be considered a regular polygon. An irregular shape is one in which all its sides are of unequal length and all its angles are of unequal measurement.
Some Solved 2D Shape Examples
Example 1: Does a rectangle fall under the category of 2D shapes? The length of a rectangle is 32 meters, and the width is 20 meters. Calculate the perimeter of this rectangle.
Solution: Yes, a rectangle belongs to the 2D shapes category. The length of the given rectangle = 32 m; width = 20 m
It is known that the perimeter of a rectangle is 2 (length + width)
P = 2 (32 + 20) = 2 (52) = 2 × 52 = 104 m
Therefore, the perimeter of the rectangle is 104 m.
Example 2: Calculate the area of a circle whose radius is 6 cm.
Solution: The area of a circle = π × r2; where π is a constant whose value is 22/7 or 3.14 and ‘r’ is the radius of the circle.
Area of the circle = π × r2
= 3.14 × 62
= 3.14 × 36
= 113.04 square cm
Example 3: Identify the shapes that are 2D in shape from the list given here
Circle, rectangular box, Rubik’s cube and a hexagon
Among the given shapes, a circle and a hexagon have no thickness or depth, so they can be classified as 2D shapes. Having three dimensions (length, width, and height) makes a rectangular box and Rubik’s cube 3D shapes.
How do children learn about 2D shapes?
In the maths curriculum, both 2D, and 3D, shapes are separate strand units, which come under the main strand of Shape and Space, but also appear in other sections of the syllabus. Beginning with junior infants, both of these strand units are taught, building on each year’s knowledge.
How to Help Children Learn about Shapes in 2D
It can be challenging to come up with engaging ways to teach kids about 2D shapes if you do not have the right resources at your disposal. It can be difficult to come up with ideas for your own resources. Here are some examples to give you an idea on how you can introduce 2D shapes in a child’s curriculum.
- Through Crafts
Use this pictorial 2D Shape activity to teach children how to put the 2D shapes together to form images. Kids love practical learning activities like this one which is both fun and educational. Children will have the opportunity to recognize different 2D shapes in everyday objects.

Reference:
https://www.twinkl.ae/resource/2d-shape-owl-cutting-skills-activity-t-tp-8088
- Through Games
Try any fun 2D shape game. Gather all students and make them part of fun interactive 2D games that help them recognize various shapes easily.
Reference: https://kristenskindergarten.com/2013/06/15/2d-shapes-game-pack/
- Video Lessons
Video lessons and clips can be very effective at engaging young learners, particularly if you enjoy using different methods of teaching. They can be great for introducing children to 2D shapes, keeping their attention.
2D Shapes in real life
In real life, shapes surround us. In nature, we can find all the possible shapes, from the droplets of rain to the roundness of oranges. In the hustle-bustle of our daily lives, we miss out on observing so many more shapes in real life.
Geometric shapes in real life are so intriguing to see, and more often than not they serve as the main indicator of an object’s identity.
All the shapes are incredibly important in the context of learning math both 2D and 3D. These shapes form the basis of geometry, and when children learn with examples, they will always remember them. We will examine some real-life shapes in the context of what we have observed in our environment.
- Hexagons- As we know by now, Hexagons typically have six straight sides of equal length. Snowflakes are an example of a Hexagonal pattern. Beehives and ice crystals are other examples of hexagons in nature.
- Rhombus in real life – A parallelogram with equal length sides is a rhombus. It is not common to see a rhombus in nature, but this one can be seen in some crystals and designer kites. But pay attention, you might even see a few more!
- Parallelogram in real life – Parallelograms are four-sided figures with two pairs of parallel sides. Erasers, clutches, and bags are examples of parallelograms in reality. The most bizarre of architecture’s structures can be described as parallelograms.
- Squares in real life – After a round or circular shape, straight sides with four right angles are the most commonly found objects that you can see around you! There are many squares you see in real life, such as rubber stamps or tiles on the floor. Coasters, chess boards, PC keys, and coasters are some of the other examples you might come across every day.
- Pentagon in real life – Despite being an unconventional 2D shape, you can see pentagons in real life. It has been used to create aesthetically pleasing figures in unique architectural creations. A common example is seeing the shape embossed on a football.
- Triangles in real life –
The three-sided figure can be seen in various objects around us in our day-to-day life. There are plenty of examples of triangles in everyday life, from the stationary we use to the yummy nachos and pizzas we eat. Even in the olden times, this shape was found in compasses and sundials.
Conclusion
Shapes are one of the fundamental mathematical topics that children need to explore. In addition to understanding the basics, they must mathematize and elaborate on their everyday knowledge so that they can communicate what they have learned. Children can benefit from learning geometry since it can be more challenging and rewarding than expected. With a better understanding of shapes, students can be more aware of their surroundings, see connections between objects, and appreciate artistic works better.
References
- https://www.math-salamanders.com/list-of-geometric-shapes.html
- https://byjus.com/maths/2d-shapes/
- https://thirdspacelearning.com/blog/what-are-2d-shapes/
- https://www.toppr.com/guides/maths/visualising-solid-shapes/2d-and-3d-figures/
- https://www.vedantu.com/maths/2d-and-3d-figures
- https://www.embibe.com/exams/2d-shapes/
- https://childhood101.com/hands-on-activities-for-learning-about-2d-3d-shapes/
Recommended Worksheets
Understanding Congruence and Similarity of 2D Figures 8th Grade Math Worksheets
Understanding the properties of rotations, reflections, and translations of 2D figures 8th Grade Math Worksheets
Shape Transformations (International Literacy Day Themed) Math Worksheets