Finding Missing Angles | Facts, Examples & Summary

Introduction

An angle is a figure formed by two rays with the same initial point. In geometry, different names are given to different angels and their combinations depending upon the type of angles they make. Different geometrical shapes such as a triangle or a quadrilateral contain a set of angles that are governed by a set of rules. For example, there are three interior angles in a triangle, the sum of which is always equal to 180^o. This means that if we are aware of two of the angles in a triangle we can find the third. Similarly using different rules and the available information we can find the missing angle in a geometrical figure.

But, before understanding different situations where we can find the missing angles, we should first recall some of the properties of different geometric shapes that will be useful in finding missing angles.

Properties of Angles in a Triangle

We know that there are three interior angles in a triangle. Let us see what are the different properties and the rules that define the relations between different angles in a triangle.

Angle Sum Property of a Triangle

The sum of the measure of the three interior angles of a triangle is always 180^o.

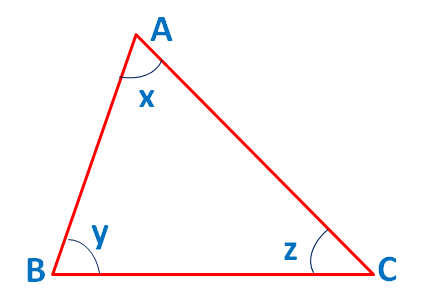
In the above triangle, ∠x + ∠y + ∠z = 180^o

Pythagoras Theorem

If one of the angles of a triangle is 90^o, the sides that make the right angle are called the base and the perpendicular while the third side is called the hypotenuse.

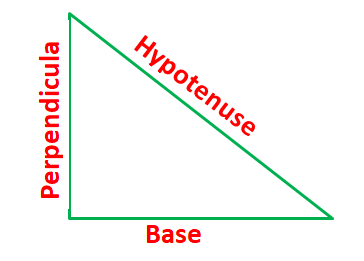
According to Pythagoras Theorem

In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides.

Mathematically,

Base² + Perpendicular² = Hypotenuse²

Therefore, if “a” is the base, “b” is the perpendicular and “c” is the hypotenuse in a right angled triangle, then

c² = a² + b²

Exterior Angle Property

According to this property, the exterior angle of a triangle is always equal to the sum of the interior opposite angles.

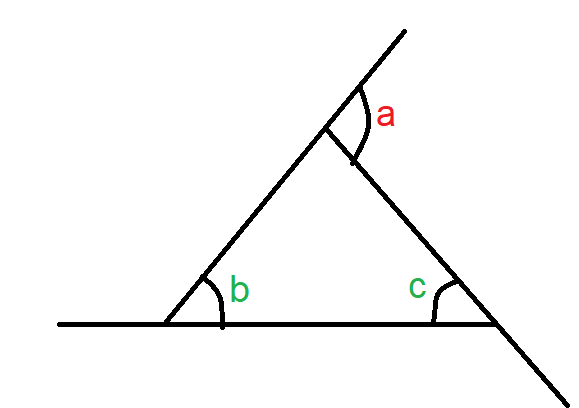
For example, in the above triangle, the exterior angle a equals the sum of the interior angles b and c.

∠a = ∠b + ∠c

Let us now look at some of the angle properties in quadrilaterals.

Properties of Angles in Quadrilaterals

We know that A quadrilateral is a closed shape that is formed by joining four points among which any three points are non-collinear. In other words, a quadrilateral is a polygon made up of four sides. Let us see what are the different properties and the rules that define the relations between different angles in quadrilaterals.

Angle Sum Property of a Quadrilateral

The sum of the measure of the three interior angles of a quadrilateral is always 360^o.

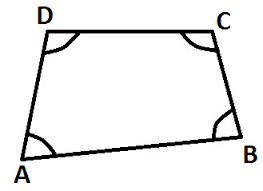
Therefore, in the above quadrilateral, ABCD, ∠A + ∠B + ∠C + ∠D = 360^o

Also, the sum of any two adjacent angles in a quadrilateral is equal to 180^o.

Angles in a Square or a Rectangle

Following properties of angles in a square or a rectangle are relevant to finding missing angles in a figure.

The interior angle of a square or a rectangle at each vertex is 90°.
The diagonals of a square or a rectangle bisect each other at 90°.

Sum of Angles of Polygons

Sum of the interior angles of a pentagon ( a quadrilateral having 5 sides ) = 540^o

Sum of the interior angles of a hexagon ( a quadrilateral having 6 sides ) = 720^o

Complementary and Supplementary Angles

Complementary angles – Two angles are said to be complementary if their sum is 90^o. For example, two angles, 30^o and 60^o are complementary because their sum, 30^o + 60^o = 90^o.

Supplementary angles – Two angles are said to be supplementary if their sum is 180^o. For example, two angles, 130^o and 50^o are supplementary because their sum, 130^o + 50^o = 180^o. Together, the supplementary angles form a straight line.

Angles Made by a Transversal with Two Lines

Let l and m be two lines and let n be the transversal intersecting them at P and Q respectively as shown below –

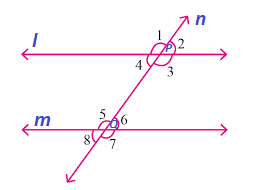
Clearly, lines l and m make eight angles with the transversal n, four at P and four at Q. we have labelled them 1 to 8 for the sake of convenience and shall now classify them in the following groups –

Exterior Angles of a Transversal

The angles whose arms do not include the line segment PQ are called exterior angles. Therefore, in the above figure, angles 1, 2, 7 and 8 are exterior angles.

Interior Angles of a Transversal

The angles whose arms include the line segment PQ are called interior angles. Therefore, in the above figure, angles 6, 4, 5 and 6 are interior angles.

Corresponding Angles in a Transversal

A pair of angles in which one arm of both the angles is on the same side of the transversal and their other arms are directed in the same sense is called a pair of corresponding angles. In the above figure, there are four pairs of corresponding angles, ∠1 and ∠ 5, ∠ 2 and ∠ 6, ∠ 3 and ∠ 7, ∠ 4 and ∠ 8.

We can also say that two angles on the same side of the transversal are known as corresponding angles if both lie either above the lines or below the two lines.

Alternate Interior Angles in a Transversal

A pair of angles in which one arm of each of the angles is on opposite sides of the transversal and whose other arms include segment PQ is called a pair of alternate interior angles. In other words, Alternate interior angles are angles formed when two parallel or non-parallel lines are intersected by a transversal. The angles are positioned at the inner corners of the intersections and lie on opposite sides of the transversal.

In the above figures, ∠ 3 and ∠ 5 form a pair of alternate interior angles. Another pair of alternate interior angles in this figure is ∠ 4 and ∠ 6.

Alternate Exterior Angles in a Transversal

A pair of angles in which one arm of each of the angles is on opposite sides of the transversal and whose other arms are directed in opposite directions and do not include segment PQ is called alternate exterior angles in a transversal.

In the above figure, ∠ 2 and ∠ 8 form a pair of alternate exterior angles. Another pair of alternate exterior angles in this figure is ∠ 1 and ∠ 7.

Now, let us use the above properties to find missing angles in different figures.

Solved Examples

Example 1 Find the measures of the angles x, y and z in the following figure –

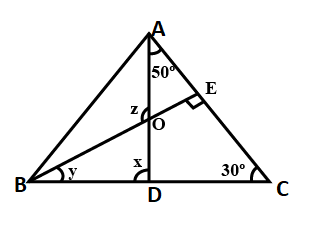
Solution We have been a figure where some of the angles are known while we are required to find the values of the angles x, y and z.

Now, let us consider the ∆ BEC.

We know that the sum of the measure of the three interior angles of a triangle is always 180^o.

Therefore,

∠ BEC + ∠ EBC + ∠ ECB = 180^o …………………………… ( 1 )

Now, we have been given that,

∠ BEC = 90^o

∠ ECB = 30^o

∠ EBC = y

Substituting these values in equation ( 1) we will get,

y + 90^o + 30^o= 180^o

⇒ y + 120^o= 180^o

⇒ y = 180^o – 120^o

⇒ y = 60^o

Now, let us consider ∆ AC.

Again, we will use that property that the sum of the measure of the three interior angles of a triangle is always 180^o.

Therefore,

∠ ADC + ∠ ACD + ∠ DAC = 180^o …………………………… ( 2 )

Now, we have been given that,

∠ DAC = 50^o

∠ ACD = 30^o

Substituting these values in equation ( 2) we will get,

∠ ADC + 50^o + 30^o= 180^o

⇒ ∠ ADC + 80^o= 180^o

⇒ ∠ ADC = 180^o – 80^o

⇒ ∠ ADC = 100^o

Now that we know the value of ∠ ADC, we can find the value of ∠ ADB.

We can see that ∠ ADC and ∠ ADE form a supplementary [air of angles. We also know that the sum of supplementary angles is always equal to180^o. Therefore,

∠ ADC + ∠ ADE = 180^o …………………….. ( 3 )

We have been given that

∠ ADE = x and we have obtained above that

∠ ADC = 100^o

Substituting these values in equation ( 3 ) we will get,

100^o + x = 180^o

⇒ x = 180^o – 100^o

⇒ x = 80^o

Now, let us consider the ∆ AOB. We can clearly see that the angle z is an exterior angle for the two angles x and y. by the definition of the exterior angle property of a triangle, The exterior angle of a triangle is always equal to the sum of the interior opposite angles. Therefore, we can say that

∠ z = ∠ x + ∠ y ………………………. ( 4 )

We have already obtained the values of and y above as –

x = 80^o

y = 60^o

Substituting these values in equation ( 4 ) we will get,

z = 80^o + 60^o

⇒ z = 140^o

Thus, we have the values of x, y and z we have as –

x = 80^o

y = 60^o

z = 140^o

Example 2 In the given figure, the lines l and m are parallel. n is a transversal and ∠ 1 = 40^o. Find all the angles marked in the figure.

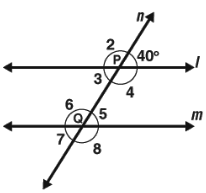
Solution We have been given that lines l and m are parallel. n is a transversal and ∠ 1 = 40^o. we need to find the remaining angles.

Let us start with each angle one by one.

First, let us find ∠ 2. We can clearly see that ∠ 1 and ∠ 2 form a supplementary pair of angles. This means that the sum of ∠ 1 and ∠ 2 should be equal to 180^o. Hence, we have,

∠ 1 + ∠ 2 = 180^o

⇒ 40^o + ∠ 2 = 180^o

⇒ ∠ 2 = 180^o – 40^o

⇒ ∠ 2 = 140^o

Now, that we have found the value of ∠ 2, we will find the value of ∠ 6

Note that ∠ 2 and ∠ 6 form a pair of corresponding angles. Since the lines that have been intersected by a transversal are parallel, therefore, the pair of corresponding angles should be equal. Hence, we have,

∠ 2 = ∠ 6 = 140^o

Similarly, ∠ 1 = ∠ 5 = 40^o

Note that ∠ 3 and ∠ 5 form a pair of alternate interior angles. Since the lines that have been intersected by a transversal are parallel, therefore, the pair of alternate interior angles should be equal. Hence, we have,

∠ 3 = ∠ 5 = 40^o

Similarly, ∠ 4 = ∠ 6 = 140^o

Similarly, we can see that ∠ 5 and ∠ 8 form a supplementary pair of angles. This means that the sum of ∠ 5 and ∠ 8 should be equal to 180^o. Hence, we have,

∠ 5 + ∠ 8 = 180^o

⇒ 40^o + ∠ 8 = 180^o

⇒ ∠ 8 = 180^o – 40^o

⇒ ∠ 8 = 140^o

Again, we can see that ∠ 6 and ∠ 7 form a supplementary pair of angles. This means that the sum of ∠ 6 and ∠ 7 should be equal to 180^o. Hence, we have,

∠ 6 + ∠ 7 = 180^o

⇒ 140^o + ∠ 7 = 180^o

⇒ ∠ 7 = 180^o – 140^o

⇒ ∠ 7 = 40^o

Hence, we have, ∠ 1 = ∠ 3 = ∠ 5 = ∠ 7 = 40^o and ∠ 2 = ∠ 4 = ∠ 6 = ∠ 8 = 140^o

Example 3 Find the missing values in the following figure –

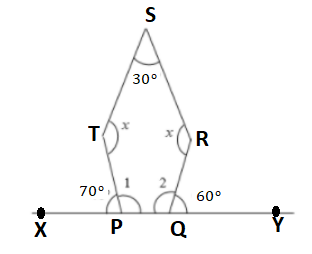
Solution We have been given a figure and we need to find the missing values in it. Let us first observe the angles that have been given to us. We have,

∠ TPX = 70^o

∠ RQY = 60^o

Now, we can see that ∠ TPX and ∠ TPQ form a pair of supplementary angles. We know that the sum of the supplementary angles is always equal to 180^o.

Therefore, we have,

∠ TPX + ∠ TPQ = 180^o ………………………. ( 1 )

Substituting the value of ∠ TPX in equation ( 1 ) we get,

∠ TPQ + 70^o= 180^o

⇒ ∠ TPQ = 180^o – 70^o

⇒ ∠ TPQ = 110^o which is the value of ∠ 1.

Again, we can see that that ∠ RQP and ∠ RQY form a pair of supplementary angles. We know that the sum of the supplementary angles is always equal to 180^o.

Therefore, we have,

∠ RQP + ∠ RQY = 180^o ………………………. ( 2 )

Also,

∠ RQY = 60^o

Subtituting the value of ∠ RQY in equation ( 2 ) we get,

∠ RQP + 60^o= 180^o

⇒ ∠ RQP = 180^o – 60^o

⇒ ∠ RQP = 120^o which is the value of ∠ 2

Now, if we see can see the figure enclosed by the points, P, Q, R, S and T form a pentagon. We also know that Sum of the interior angles of a pentagon is always equal to 540^o.

Therefore, we have,

∠ PQR + ∠ QRS + ∠ RST + ∠ STP +∠ TPQ = 540^o ………………………. ( 3 )

Also, we have,

∠ PQR = 120^o ( as calculated above)

∠ QRS = x ( given in the question )

∠ RST = 30^o ( given in the question )

∠ STP = x ( given in the question )

∠ TPQ = 110^o( as calculated above)

Substituting these values in equation ( 3 ), we will get,

120^o + x + 30^o +x + 110^o = = 540^o

⇒ 2x + 260^o = 540^o

⇒ 2x = 540^o – 260^o

⇒ 2x = 280^o

⇒ x = 140^o

Hence, the missing angles in the figure are –

x = 140^o

∠ TPQ = ∠ 1 = 110^o

∠ TPQ = ∠ 2 = 110^o

Key Facts and Summary

The sum of the measure of the three interior angles of a triangle is always 180^o.
If one of the angles of a triangle is 90^o, the sides that make the right angle are called the base and the perpendicular while the third side is called the hypotenuse.
The exterior angle of a triangle is always equal to the sum of the interior opposite angles.
The sum of the measure of the three interior angles of a quadrilateral is always 360^o.
Sum of any two adjacent angles in a quadrilateral is equal to 180^o.
The interior angle of a square or a rectangle at each vertex is 90°.
The diagonals of a square or a rectangle bisect each other at 90°.
Sum of the interior angles of a pentagon ( a quadrilateral having 5 sides ) = 540^o
Sum of the interior angles of a hexagon ( a quadrilateral having 6 sides ) = 720^o
Two angles are said to be complementary if their sum is 90^o.
Two angles are said to be supplementary if their sum is 180^o.
Alternate interior angles are angles formed when two parallel or non-parallel lines are intersected by a transversal.
A pair of angles in which one arm of each of the angles is on opposite sides of the transversal and whose other arms are directed in opposite directions and do not include segment PQ is called alternate exterior angles in a transversal.

Recommended Worksheets

Straight Angles (Farmers’ Day Themed) Math Worksheets
Acute Angles (Sports Themed) Math Worksheets
Reflex Angles (International Artists’ Day Themed) Math Worksheets

Browse All Worksheets

We spend a lot of time researching and compiling the information on this site. If you find this useful in your research, please use the tool below to properly link to or reference Helping with Math as the source. We appreciate your support!