What is a perimeter?
Perimeter is a closed path that covers or surrounds any two-dimensional shape. We can say that a perimeter is the total distance of any closed shape. Here are the examples of shapes that we can determine its perimeter.
How to find the perimeter?
Finding the perimeter of any two-dimensional shape depends on the number of sides our shape has. Say, for example, we have a triangle and a square. The number of sides a triangle has is 3; hence, we will get the total distance around its three sides.
Now, how do we find the perimeter? Well, we need to start identifying the shape of our figure first, then use a formula in getting the perimeter. Each shape has a different formula in determining the perimeter – and that’s what we will tackle in the next sections.
Circle
The perimeter of a circle is called as the circumference. A circle is still considered a two-dimensional shape even though it does not have a length and width. However, they have radius and diameter. We can determine the circumference of any circle through its radius or diameter.
Finding the Perimeter of a Circle through Radius
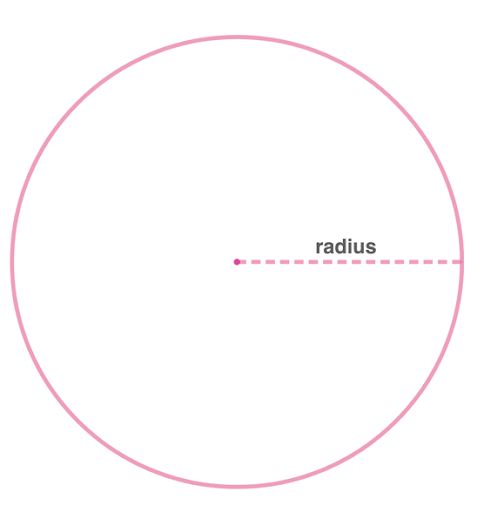
The radius is the distance from the center of the circle to any point on the circumference. The image shows the radius of a circle.
Now, to get the circumference of a circle using its radius, we will use the formula
C= 2πr
where C = circumference,
= 3.14 or $\frac{22}{7}$
r = radius
Example #1
What is the circumference of a circle if the radius is 18 cm?
Solution
| Step-by-step Process | Explanation |
| C=2πr | Write the formula for finding the circumference of a circle given a radius. |
| C=2π(18 cm) | Substitute the value of the radius, which is 18 centimeters. |
| C = (2)(3.14)(18 cm) | Write the value of π, which is 3.14. |
| C = 113.04 cm | Multiply. |
| Therefore, the circumference of a circle with a radius of 18 cm is 113.04 cm. |
Example #2
Find the total distance around the circle with a radius that measures 30 meters.
Solution
| Step-by-step Process | Explanation |
| C=2πr | Write the formula for finding the circumference of a circle given a radius. |
| C=2π(30 m) | Substitute the value of the radius, which is 30 meters. |
| C = (2)(3.14)(30 m) | Substitute the value of π, which is 3.14. |
| C = 188.4 m | Multiply. |
| Therefore, the circumference of a circle with a radius of 30 m is 188.4 m. |
Finding the Perimeter of a Circle through its Diameter

The diameter is the longest line segment in any circle. The measure of a diameter is twice the measure of a radius. Hence, the formula of finding the circumference of a circle through its diameter is given by:
C= πd
where C = circumference,
= 3.14 or $\frac{22}{7}$
d = diameter
Example #1
What is the circumference of a circle with a diameter of 13 mm?
Solution
| Step-by-step Process | Explanation |
| C=πd | Write the formula for finding the circumference of a circle given a diameter. |
| C=π(13 mm) | Substitute the value of the radius, which is 13 millimeters. |
| C = (3.14)(13 mm) | Substitute the value of π, which is 3.14. |
| C = 40.82 | Multiply. |
| Therefore, the circumference of a circle with a diameter of 13 mm is 40.82 mm. |
Example #2
Determine the total distance around the circle when the diameter is 46 decimeters.
Solution
| Step-by-step Process | Explanation |
| C=πd | Write the formula for finding the circumference of a circle given a diameter. |
| C=π(46 dm) | Substitute the value of the radius, which is 46 decimeters. |
| C = (3.14)(46 dm) | Substitute the value of π, which is 3.14. |
| C = 144.44 dm | Multiply. |
| Therefore, the circumference of a circle with a diameter of 46 dm is 144.44 dm. |
Triangle
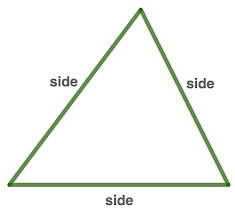
A triangle is a two-dimensional closed shape with three straight sides. Every triangle has three sides, three vertices, and three angles. If given a triangle, we simply add all the measures of its sides.
The formula in finding the perimeter of a triangle is given by
P = a + b + c
where a, b, and c are the measures of the sides of a triangle.
Example #1
If the measures of the sides of a triangle are 17 cm, 23 cm, and 25 cm, what is its perimeter?
Solution
| Step-by-step Process | Explanation |
| P = a + b + c | Write the formula for finding the perimeter of any triangle. |
| P = 17 cm + 23 cm + 25 cm | Since the measure of its sides is 17 cm, 23 cm, and 25 cm, we will simply substitute it to a, b, and c. |
| P = 65 cm | Get the sum of the sides. |
| Therefore, the perimeter of a triangle with side measures of 17 cm, 23 cm, and 25 cm is 65 cm. |
Example #2
Can you determine the perimeter of a triangle if all three sides measure 19 meters?
Solution
| Step-by-step Process | Explanation |
| P = a + b + c | Write the formula for finding the perimeter of any triangle. |
| P = 19 m + 19 m + 19 m | Since the sides of the triangle are equal, we will simply add 19 three times. Alternatively, we can get the perimeter of an equilateral triangle by multiplying the measure of the side by 3. Hence,P = 3 x 19 mP = 57 m |
| P = 57 m | Get the sum of the sides. |
| Therefore, the perimeter of a triangle where all sides measure 19 meters is 65 cm. |
Quadrilaterals
A quadrilateral is any polygon with exactly four sides. There are different kinds of quadrilaterals such as square, rhombus, rectangle, trapezoid, and rhombus.
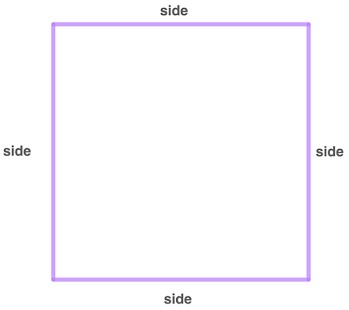
Square
A square is a quadrilateral where each of its sides is equal. Hence, we can get the perimeter of a square by adding the measures of all four sides or by simply multiplying the measure of one side by 4.
Thus, the formula of finding the perimeter of the square is:
P = 4s
where s is the measure of the side of a square.
Example #1
What is the perimeter of a square where each side measures 10 centimeters?
Solution
| Step-by-step Process | Explanation |
| P = 4s | Write the formula for finding the perimeter of a square. |
| P = (4)(10 cm) | Substitute the value of the side measure where s = 10 cm. |
| P = 40 cm | Multiply 4 by 10. |
| Therefore, the perimeter of the square with a side measure of 10 cm is 40 cm. |
Example #2
Determine the total distance around a square where one side measures 27 meters.
Solution
| Step-by-step Process | Explanation |
| P = 4s | Write the formula for finding the perimeter of a square. |
| P = (4)(27 m) | Substitute the value of the measure of the side where s is 27 meters. |
| P = 108 m | Multiply 4 by 27. |
| Therefore, the perimeter of the square with a side measure of 27 meters is 108 meters. |
Rhombus
Like squares, a rhombus is a quadrilateral where four sides are equal, and the pair of opposite sides are parallel to each other. Hence, the formula in finding the perimeter of a rhombus is the same as finding the perimeter of a square.
Thus, it is given by the formula
P = 4s
where s is the measure of the side of a rhombus.
Example #1
What is the perimeter of a rhombus if the measure of one side is 9 units?
Solution
| Step-by-step Process | Explanation |
| P = 4s | Write the formula for finding the perimeter of a rhombus. |
| P = (4)(9 units) | Substitute the value of the measure of the side where s is 9 units. |
| P = 36 units | Multiply 4 by 9. |
| Therefore, the perimeter of the rhombus with a side measure of 9 units is 36 units. |
Example #2
Find the total distance of a rhombus with a side measure of 35 kilometers.
Solution
| Step-by-step Process | Explanation |
| P = 4s | Write the formula for finding the perimeter of a rhombus. |
| P = (4)(35 km) | Substitute the value of the measure of the side where s is 35 kilometers. |
| P = 140 kilometers | Multiply 4 by 35. |
| Therefore, the perimeter of the rhombus with a side measure of 35 kilometers is 140 kilometers. |
Rectangle
A rectangle is a two-dimensional quadrilateral where opposite sides are parallel and equal. The sides of a rectangle are called as a width and length. Thus, the formula given in getting the perimeter of a rectangle is:
P = 2(l + w)
where l = length
w = width
Example #1
What is the perimeter of a rectangle if the length measures 19 centimeters and the width measures 21 centimeters?
Solution
| Step-by-step Process | Explanation |
| P = 2(l + w) | Write the formula for finding the perimeter of a rectangle. |
| P = (2)(19 cm + w) | Substitute the value of the length which is 19 centimeters. |
| P = (2)(19 cm + 21 cm) | Substitute the value of the width which is 21 centimeters. |
| P = (2)(40 cm) | Add 19 cm and 21 cm. Thus, 19 cm + 21 cm = 40 cm |
| P = 80 cm | Multiply 2 by 40 cm. |
| Therefore, the perimeter of a rectangle with lengths and widths of 19 cm and 21 cm is 80 centimeters. |
Example #2
Determine the perimeter of a rectangle if the length measures 350 centimeters and the width measures 3 meters.
Solution
| Step-by-step Process | Explanation |
| 3 m x $\frac{100 cm}{1 m}$ = 300 cm | Convert meters to centimeters. Note that before finding the perimeter of any shape, always make sure that the unit of measurement is always the same. |
| P = 2(l + w) | Write the formula for finding the perimeter of a rectangle. |
| P = (2)(350 cm + w) | Substitute the value of the length which is 350 centimeters. |
| P = (2)(350 cm + 300 cm) | Substitute the value of the width which is 300 centimeters. |
| P = (2)(650 cm) | Add 350 cm and 300 cm. |
| P = 1300 cm | Multiply 2 by 650 cm. |
| Therefore, the perimeter of a rectangle with lengths and widths of 350 cm and 300 cm is 1300 centimeters. |
Regular Polygon
Regular polygons are two-dimensional geometric figures with a fixed number of sides and where all sides are equal.
Hence, the formula of finding the perimeter of any regular polygon is given by:
P = n(s)
where n = number of sides of a regular polygon
s = measure of the side of a regular polygon
Example #1
What is the perimeter of a 9-sided polygon with side measures of 23 meters?
Solution
| Step-by-step Process | Explanation |
| P = n(s) | Write the formula for finding the perimeter of a regular polygon. |
| P = (9)(s) | Since we have a 9-sided polygon, substitute n by 9. |
| P = (9)(23 m) | Substitute the side measure of a regular polygon to s. |
| P = 207 m | Multiply 9 by 23. |
| Therefore, the perimeter of a regular polygon with 9 sides is 207 meters. |
Example #2
Determine the perimeter of a five-sided regular polygon where each side measures 11 centimeters.
Solution
| Step-by-step Process | Explanation |
| P = n(s) | Write the formula for finding the perimeter of a regular polygon. |
| P = (5)(s) | Since we have a 5-sided polygon, substitute n by 5. |
| P = (5)(11 cm) | Substitute the side measure of a regular polygon to s. |
| P = 55 cm | Multiply 5 by 11. |
| Therefore, the perimeter of a 5-sided regular polygon is 55 centimeters. |
What is the formula for finding the perimeter of some closed-shape?
The table below shows the formula for finding the perimeter of some closed-shape.
| 2D-Shape | Formula |
| Circle | C = 2r, where r is the radius orC = d, where d is the diameter |
| Triangle | P = a + b + c where a, b, and c are the measure of the sides of the triangle |
| Square or Rhombus | P = 4swhere s is the measure of the sides of the square or rhombus |
| Rectangle | P = 2(l + w)where l is the length and w is the width |
| Regular Polygon | P = n(s)where n is the number of the sides of a polygon and s is the measure of the sides. |
How to solve problems involving perimeter?
To solve problems that involve finding the perimeter of any closed shape, you may follow the following steps:
- Identify the shape being described.
- Make sure that the unit of measurement is always the same.
- Use the formula for finding the perimeter of the given shape.
- Always remember to write the proper unit of measurement.
Problem #1
A rectangular field garden measures 45 yards by 60 yards. What is the total distance that surrounds the garden?
Solution
| Step-by-step Process | Explanation |
| P = 2(l + w) | Write the formula for finding the perimeter of a rectangle. |
| P = (2)(45 yd + w) | Substitute the value of the length which is 45 yards. |
| P = (2)(45 yd + 60 yd) | Substitute the value of the width which is 21 centimeters. |
| P = (2)(105 yd) | Add 45 yd and 60 yd. Thus, 45 yd + 60 yd = 105 yd |
| P = 210 yd | Multiply 2 by 105 yd. |
| Therefore, the perimeter of a rectangle with lengths and widths of 45 yards and 60 yards is 210 yards. |
Problem #2
The diameter of a clock measures 10 inches. What is the circumference of the clock?
Solution
| Step-by-step Process | Explanation |
| C=πd | Write the formula for finding the circumference of a circle given a diameter. |
| C=π(10 in) | Substitute the value of the radius, which is 10 inches. |
| C = (3.14)(10 in) | Substitute the value of π, which is 3.14. |
| C = 31.4 in | Multiply. |
| Therefore, the circumference of a circle with a diameter of 10 inches is 31.4 inches. |
Problem #3
A seven-sided regular polygon with a side measure of 13 decimeters is needed for Gwyneth’s project. What is the total distance that surrounds the polygon?
Solution
| Step-by-step Process | Explanation |
| C=πd | Write the formula for finding the circumference of a circle given a diameter. |
| C=π(10 in) | Substitute the value of the radius, which is 10 inches. |
| C = (3.14)(10 in) | Substitute the value of π, which is 3.14. |
| C = 31.4 in | Multiply. |
| Therefore, the circumference of a circle with a diameter of 10 inches is 31.4 inches. |
What is the importance of finding the perimeter?
The use of perimeter is used in our daily lives, especially architects and engineers. Most people who understand the concept of the perimeter can help them design their room, remodel their kitchen, or even build a table or chair. Farmers, gardeners, or even lot owners also use their knowledge in perimeter to fence their lots. More so, perimeters are important in estimating and calculating materials needed for completing a certain projects.
Recommended Worksheets
Perimeter of a Pentagon (Valentine’s Day Themed) Math Worksheets
Perimeter of a Hexagon (Rio Carnival Themed) Math Worksheets
Perimeter of Trapezoid (Lantern Festival Themed) Math Worksheets









