Introduction
We have a number of figures in mathematics that are so evenly balanced n different sizes and shapes. Let us observe the following figures –
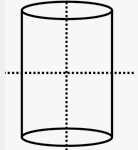
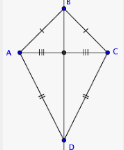
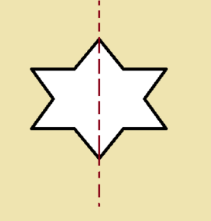
We can observe that for each figure the one half on one side of the dotted line is exactly identical to the one half on the other side of the dotted line. In other words, we can say that the two halves are mirror images of each other. In fact, if we place a mirror on the dotted line then the image of one side of the figure is exactly the same as the figure on the other side of the dotted line then the image of one side. This means that each figure is divided into two identical parts about the dotted line. When we fold these figures along the dotted line, one-half of the figures would fit exactly over the other half. The dotted line is known as the line of symmetry. So, how do we define the line of symmetry?
What is Line is Symmetry?
We say that a given line has a line of symmetry or it is symmetrical about a line if the line divides a given figure into two identical halves. The line is called the axis of symmetry or line of symmetry.
Types of Line Symmetry
There are two types of line symmetries according to which we can classify the symmetries in different geometrical figures. These types are –
- Horizontal Lines of Symmetry
- Vertical Line of Symmetry
Let us discuss them in detail
Horizontal Line of Symmetry
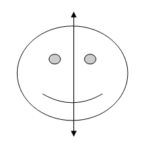
If the line of symmetry is such that it divides a geometrical shape into two identical halves in a horizontal manner, it is known as a horizontal line of symmetry. In other words, a horizontal line of symmetry is that line that runs across the image thus dividing into two identical halves. This line may also be called a sleeping straight line that parts an image or shape into identical halves.
Vertical Line of Symmetry
If the line of symmetry is such that it divides a geometrical shape into two identical halves in a vertical manner, it is known as a vertical line of symmetry. In other words, a vertical line of symmetry is that line that runs down an image thus dividing it into two identical halves. This means that a vertical line of symmetry is a straight standing line that divides an image or shape into two identical halves.
Let us now discuss the number of lines of symmetry of different geometrical figures.
1 Line Symmetry
A geometrical figure is said to have one line of symmetry if it is symmetrical about one line of axis only. Let us consider some examples.
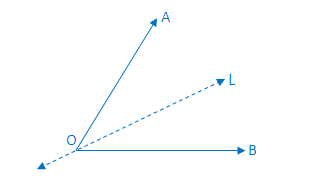
The symmetry of an Angle
An angle with equal arms has one line of symmetry which is along the internal bisector of the angle.
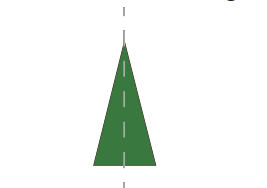
The symmetry of an Isosceles Triangle
An isosceles triangle has one line of symmetry which is along the median through the vertex. This is because a triangle is only said to be an isosceles triangle if it has 2 equal sides. Therefore, every isosceles triangle by definition has 1 line of symmetry. This line of symmetry can be drawn by joining the vertex between equal sides and the midpoint of the opposite side.
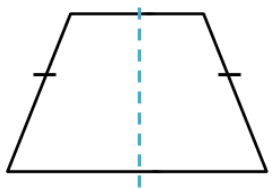
The symmetry of an Isosceles Trapezium
An isosceles trapezium has two parallel sides and two non-parallel sides of equal length it has only one line of symmetry along the line segment joining the midpoints of the two parallel sides. A trapezium is a four-sided, two-dimensional shape having two of its sides parallel to each other. A regular trapezium or also known as a proper trapezium is a trapezium having one pair of opposite sides parallel but the other two sides need not be equal to each other. Now, when a shape is folded and it sits completely on top of itself, then the fold line is called a line of symmetry. Now, isosceles trapeziums are those trapeziums having one pair of opposite sides parallel and the other pair of opposite sides equal. In fact, they are just like isosceles triangles.
The symmetry of a Kite
A kite has one line of symmetry along with one of its diagonals. A kite is a quadrilateral with two different pairs of adjacent sides that are equal in length
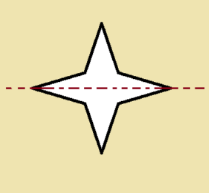
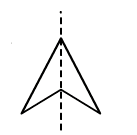
The symmetry of an arrowhead
An arrowhead has one line of symmetry.
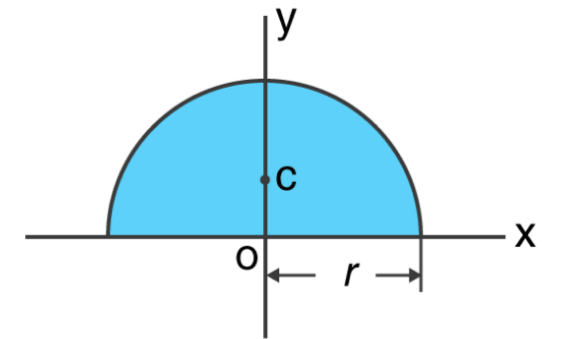
The symmetry of a Semi-Circle
A semi-circle has only one line of symmetry perpendicular to the perpendicular bisector of its diameter. This is because the line of symmetry of a semicircle is half of a circle, which has only one line of symmetry.
2 Lines Symmetry
A geometrical figure is said to have two lines of symmetry if it is symmetrical about two lines of axis only. Let us consider some examples.
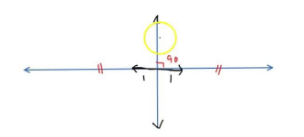
The symmetry of a Line Segment
A line segment has two lines of symmetry, namely the segment itself and the perpendicular bisector of the segment.
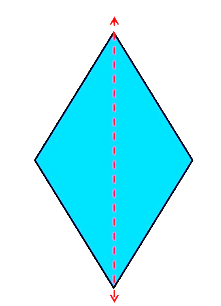
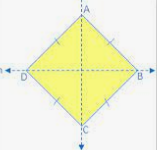
The symmetry of a Rhombus
A rhombus has two lines of symmetry along the diagonals of the rhombus. This is because a rhombus has four equal sides but of varying angles. This allows a rhombus to have two lines of symmetry, one in a horizontal manner while the other in a vertical manner, which makes it an order of two, along with an angle of rotation of 180 degrees.
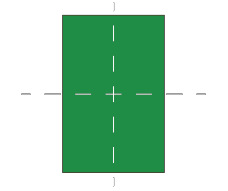
The symmetry of a Rectangle
A rectangle has two lines of symmetry along the line segment joining the midpoints of the opposite sides. This is because a rectangle is a 4 sided polygon whose two opposite sides are equal and parallel. The angles of a rectangle are always 90 degrees and its diagonals are always equal. Hence, the lines of symmetry in a rectangle cut its opposite sides into equal parts. It is important to note that a rectangle cannot have a diagonal line of symmetry like a square because the sides are not the same length.
3 Lines Symmetry
A geometrical figure is said to have three lines of symmetry if it is symmetrical about three lines of axis only. Let us consider some examples.
The symmetry of an Equilateral Triangle
An equilateral triangle has three lines of symmetry Along three medians this is because A triangle is said to be an equilateral triangle only if all its three sides are equal which also means that it has three equal angles therefore it has three lines of symmetry along its three medians

4 Lines Symmetry
A geometrical figure is said to have four lines of symmetry if it is symmetrical about four lines of axis only. Let us consider some examples.
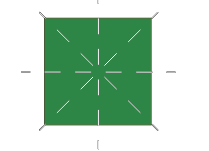
The symmetry of a Square
A square has four lines of symmetry two a long line segment joining the midpoints of opposite sides and two along the diagonals. In other words, both the diagonals and the lines joining the midpoints of their opposite sides, that is the bisectors form symmetrical lines in a square.
5 Lines Symmetry
A geometrical figure is said to have five lines of symmetry if it is symmetrical about five lines of axis only. Let us consider some examples.
The symmetry of a Regular Polygon
A regular pentagon has five lines of symmetry. This is because a regular pentagon has five sides that are all equal. So, it contains five symmetry lines.

6 Lines Symmetry
A geometrical figure is said of having six lines of symmetry if it is symmetrical about six lines of axis only. Let us consider some examples.
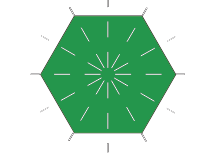
The symmetry of a Regular Hexagon
A regular hexagon has six lines of symmetry. This is because a regular hexagon has six sides that are all equal. So, it contains six symmetry lines. In other words, a regular hexagon has its entire six sides equal and each of its angles measures 120o. three symmetrical lines are present along the lines joining the midpoints of opposite sides and three are present along the diagonals.
Infinite Lines of Symmetry
A geometrical figure is said of having infinite lines of symmetry if it is symmetrical about infinite lines of the axis. Let us consider some examples.
The symmetry of a Line
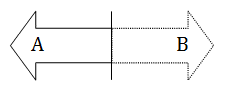
A line has a finite length and hence it can be considered that each line perpendicular to the given line divides the line into equal halves ( parts ). So, a line has an infinite number of symmetrical lines which are perpendicular to it. So, a line has an infinite number of symmetrical lines which are perpendicular to it. Also, a line is symmetrical to itself.
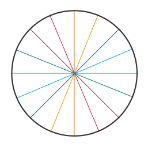
The symmetry of a Circle
A circle has an infinite number of lines of symmetry all along the diameters. SA circle has its diameter as the line of symmetry, and a circle can have an infinite number of diameters. Therefore, a circle has infinite lines of symmetry.
Examples of Symmetry in Real Life
Below we have a list of activities that we can observe around our homes or in our neighbourhood which will help us understand symmetry.
- Symmetry at the Supermarket
Have you ever observed the symmetry at the supermarket? If we look around in a supermarket we will observe we can identify boxes, containers as well as packages that are symmetrical in shape.
- Symmetry in Fruits and Vegetables
Let us now recall the shapes of different fruits and vegetables. Can we say that some of the vegetables and fruits that we make use of every day are asymmetrical in nature? For many apples and oranges can be said of different lines of symmetry.
- Symmetry in Nature
Let us now recall different types of flowers, trees, leaves for symmetry. We can notice a number of leaves and flowers that are symmetrical in shape.
- Symmetry in Your Bedroom
Look at the lines of symmetry on your bed, TV, video game system, computer and closet door. Can you observe that most of the furniture in your house or workspace is symmetrical in shape?
- Kitchen Symmetry
Similar to the bedroom we can observe symmetry in the boxes or containers in the kitchen cupboards.
Line of Symmetry of English alphabets
Let us now discuss the line of symmetry of some English alphabets.
The symmetry of the capital alphabet “ A ”
The capital alphabet “ A ” has one vertical line of symmetry which is along the central bisector of the alphabet.

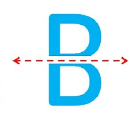
The symmetry of the capital alphabet “ B ”
The capital alphabet “ B ” has one horizontal line of symmetry which is along the central bisector of the alphabet.
The symmetry of the capital alphabet “ C ”
The capital alphabet “ C ” has one horizontal line of symmetry which is along the central bisector of the alphabet.

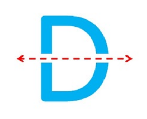
The symmetry of the capital alphabet “ D ”
The capital alphabet “ D ” has one horizontal line of symmetry which is along the central bisector of the alphabet.
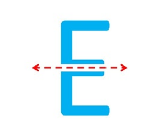
The symmetry of the capital alphabet “ E ”
The capital alphabet “ E ” has one horizontal line of symmetry which is along the central bisector of the alphabet.
The symmetry of the capital alphabet “ H ”
The capital alphabet “ H ” has one horizontal line of symmetry as well as one vertical line of symmetry which is along the central bisector of the alphabet.
The symmetry of the capital alphabet “ I ”
The capital alphabet “ I ” has one horizontal line of symmetry as well as one vertical line of symmetry which is along the central bisector of the alphabet.
The symmetry of the capital alphabet “ K ”
The capital alphabet “ K ” has one horizontal line of symmetry which is along the central bisector of the alphabet.

Similarly, we can observe the symmetries of other alphabets as –

Asymmetrical Shapes
It is not that every geometrical shape is symmetrical in nature. There are many shapes that have no symmetry at all. Such shapes are said to have no line of symmetry. Hence, a geometrical figure is said of having no line of symmetry if it is not symmetrical about any line of axis. Let us consider some examples.
The symmetry of a Parallelogram
A parallelogram has no line of symmetry. This is because the shape of a parallelogram is such that it cannot be divided into two identical halves in any manner.

The symmetry of a Scalene Triangle
A scalene no line of symmetry. This is because a triangle is said to be scalene if none of its two sides is equal. Hence, there cannot be any line through any vertex of the scalene triangle through which a median can be drawn that bisects the triangle into two halves. Hence a scalene triangle has no line of symmetry.
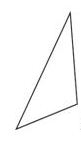
Similarly, the octagon is symmetrical. If you fold it where the line is, each side would match perfectly. But how do you know when a figure is NOT symmetrical? Look at the example below. This figure is not symmetrical. Can you figure out why?
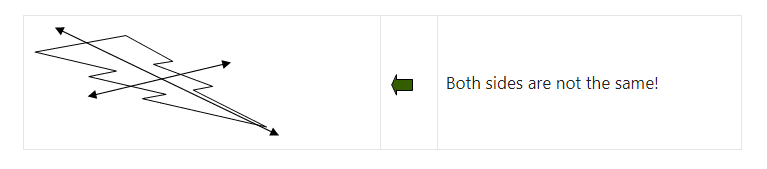
The lightning bolt is not symmetrical because it does not split in half with two equal sides. One simple way to see if a figure is symmetrical is to draw it on paper and fold it in half. If the sides match completely, it is symmetrical.
Key Facts and Summary
- A given line has a line of symmetry or it is symmetrical about a line if the line divides a given figure into two identical halves. The line is called the axis of symmetry or line of symmetry.
- There are two types of lien symmetries according to which we can classify the symmetries in different geometrical figures – Horizontal Lines of Symmetry and Vertical Line of Symmetry
- If the line of symmetry is such that it divides a geometrical shape into two identical halves in a horizontal manner, it is known as a horizontal line of symmetry.
- If the line of symmetry is such that it divides a geometrical shape into two identical halves in a vertical manner, it is known as a vertical line of symmetry.
- A geometrical figure is said of having one line of symmetry if it is symmetrical about one line of axis only.
- A geometrical figure is said of having two lines of symmetry if it is symmetrical about two lines of axis only.
- A geometrical figure is said of having three lines of symmetry if it is symmetrical about three lines of axis only.
- A geometrical figure is said of having three lines of symmetry if it is symmetrical about three lines of axis only.
- A geometrical figure is said of having four lines of symmetry if it is symmetrical about four lines of axis only.
- A geometrical figure is said of having five lines of symmetry if it is symmetrical about five lines of axis only.
- A geometrical figure is said of having infinite lines of symmetry if it is symmetrical about infinite lines of the axis. Let us consider some examples.
- A geometrical figure is said of having no line of symmetry if it is not symmetrical about any line of axis.
Recommended Worksheets
Complementary Angles (Lantern Festival Themed) Math Worksheets
Area of a Rhombus (April Fool’s Day Themed) Math Worksheets
Perimeter of a Square (New Year’s Day Themed) Math Worksheets









