Introduction
Welcome to the exciting world of geometry! Today, we’ll dive into a fascinating topic: solid shapes’ surface area. But before we go further, let’s think about something. Have you ever wondered how much wrapping paper you’d need to cover a birthday gift? How much paint would you need to paint a cube or a sphere? Well, these are the sorts of questions that the concept of surface area can help us answer!
Grade Appropriateness
The concept of surface area is typically taught to students around 5th to 7th grade, making it perfect for children ages 10 to 12. However, if you’re a little younger or older, don’t worry. This subject is fascinating for everyone, and we will ensure it’s easy to understand.
Math Domain
This topic falls under the domain of Geometry. Shapes, their properties, and their spaces are the focus of the math discipline of geometry.
Applicable Common Core Standards
Here are the Common Core Standards that apply to the surface area of solid shapes:
CCSS.MATH.CONTENT.6.G.A.2: Find the volume of a right rectangular prism with fractional edge lengths by packing it with unit cubes of the appropriate unit fraction edge lengths, and show that the volume is the same as would be found by multiplying the edge lengths of the prism. Apply the formulas V = l w h and V = b h to find volumes of right rectangular prisms with fractional edge lengths in the context of solving real-world and mathematical problems.
CCSS.MATH.CONTENT.7.G.B.6: Solve real-world and mathematical problems involving area, volume, and surface area of two- and three-dimensional objects composed of triangles, quadrilaterals, polygons, cubes, and right prisms.
Definition of the Topic
The surface area is a measurement of the overall space that the object’s surface takes up. In simpler words, it is the area of the ‘skin’ of the shape. Like our skin covers our body, the surface area covers a shape.
Key Concepts
When learning about surface area, it is essential to understand the following basic ideas:
Surface Area of a Cube: Since a cube has six equal sides, to find the total surface area, we calculate the area of one side (length × length) and then multiply it by 6.
Surface Area of a Rectangular Prism: Since a rectangular prism has three different pairs of equal sides, we find the area of each pair and then add them all together.
A rectangular prism has six faces which aren’t all the same.
Surface Area of a Cylinder: We find the total surface area by adding the area of the two circles and the area of the curved surface. A cylinder has two circles (one at the top, one at the bottom) and a curved surface around it.
Surface Area of a Sphere: The sphere’s total surface area is four times πr². A sphere has a curved surface all around it.
Surface Area of a Cone: A cone’s total surface area is the sum or total of the area of the base (circular) and the curved surface. A cone has a circle (the base) and a curved surface.
Discussion with Illustrative Examples
Three-dimensional objects with length, width, and height are known as solid figures—pyramids, prisms, cones, spheres, and other commonly recognizable solid shapes.
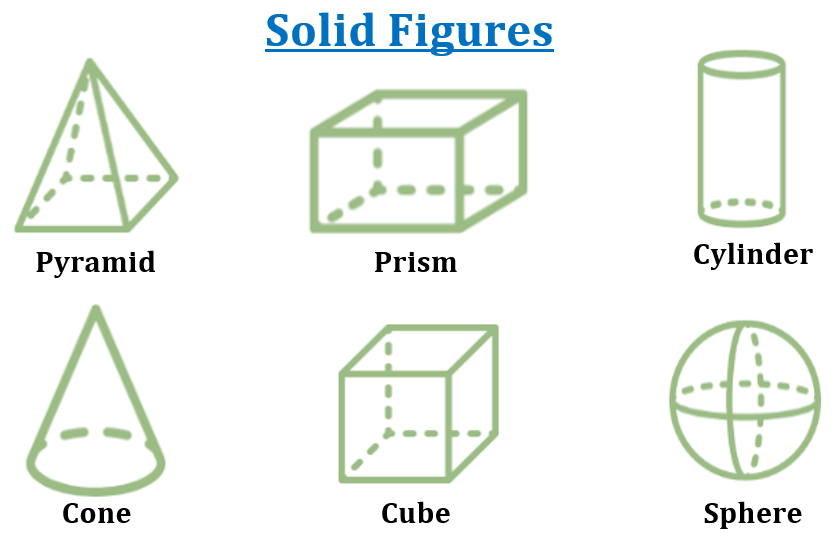
Formulas of Getting the Surface Area
The surface area is a measurement of the overall space that the object’s surface takes up.
| Solid Figure | Formula |
| Cube (with side length,s) | 6s2 |
| Rectangular Prism (with length, l, width, w, and height, h) | 2 (lw +lh +wh) |
| Regular Square Pyramid (with a perimeter of the base, P, area of the base, B, and slant height, s) | ½ Ps + B |
| Cone (with slant height = s and radius = r) | πr2 + πrs |
| Sphere (with radius, r) | 4πr2 |
| Cylinder (with radius, r, and height, h) | 2πr2 + 2πrh |
Let’s dive into some examples!
Cube: Suppose you have a cube with each side measuring 4 cm.
The cube’s face has an area of 4 cm × 4 cm = 16 cm².
Since a cube has six faces, the total surface area is 16 cm² × 6 = 96 cm².
Rectangular Prism: Consider a rectangular prism (like a box) with length = 5 cm, width = 3 cm, and height = 4 cm. The surface area is found by calculating the area of all faces:
2 (lw + lh + wh) = 2 [(5×3) + (5×4) + (3×4)]
2 (15 + 20 + 12) = 94 cm².
Cylinder: Say you have a cylinder with a radius = 3 cm and a height = 7 cm; its surface area would be calculated using the formula 2πr(h + r).
It will be ( 2 × 3.14× 3 )(7 + 3) = 188.4 cm².
Sphere: For a sphere with r = 4 cm, the surface area would be calculated using the formula 4πr², resulting in 4 × 3.14 × 42 = 200.96 cm².
Cone: Say we have a cone with a base radius of 2 cm and a slant height of 5 cm; the lateral surface area (without the base) is calculated using the formula πrs, where s is the slant height. So, the lateral surface area would be 3.14 × 2 × 5 = 31.4 cm².
The area of its base is calculated using πr2, which gives us 3.14 × 22 = 12.56 cm2.
Thus, the total surface area of the cone is 31.4 cm2 + 12.56 cm2 = 43.96 cm2.
Examples with Solutions
Example 1
Calculate the surface area of the solid figure below.
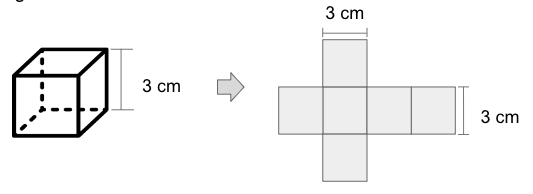
Solution
Since a cube has square faces, all sides are 3 cm in measure.
When you cut a cube and make it a flat figure, the image below will likely be the result.
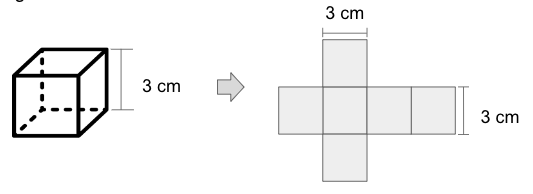

Thus, the total surface area of the cube is 54 cm2.
Example 2
Calculate the surface area of the solid figure below.
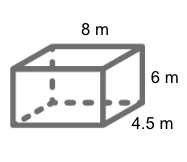
Solution
Since l = 8 m, h = 6 m, and w = 4.5 m then,
Surface Area = 2 (lh + lw +hw)
Surface Area = 2[(8 m)(6 m) + (8 m)(4.5 m) + (6 m)(4.5 m)]
Surface Area = 2 (48 + 36 + 27) sq.m
Surface Area = 2 (111) sq. m
Surface Area = 222 sq. m
Therefore, the total surface area of the rectangular prism is 222 m2.
Example 3
Solve for the surface area of the square pyramid below.
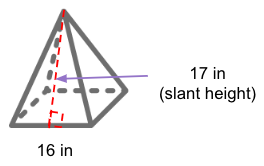
Solution
Using the formula ½ Ps + B where P is the perimeter of the base, s is the slant height, and B is the area of the base, we have,
P = 16 in × 4 = 64 inches (perimeter of the base)
B = 16 in × 16 in = 256 sq. inches (area of the square base)
Surface Area = ½ Ps + B = ½ (64 in)(17 in) + 256 sq. in = 800 sq. inches
We may also get the square pyramid’s total surface area by adding the base’s area and its lateral surface area. The lateral surface area consists of the regions of the four triangles calculated using 4 ( ½ × 16 × 17 ) = 544 sq. in
TSA = B + LSA
TSA = 256 sq. in + 544 sq. in
TSA = 800 sq. in
Hence, the total surface area of the regular square pyramid is 800 sq. inches.
Real-Life Application with Solution
Let us see how you could use this in a real-life scenario!
Suppose you want to paint a cylindrical can with the following dimensions: a radius of 5 cm and a height of 10 cm. How much area will you have to paint? We can find this out using our surface area formulas!
The cylinder’s surface area is 2πr(h + r). So, in this case, it’s (2 × 3.14 × 5) (10 + 5) = 471 cm². Therefore, you will need enough paint to cover 471 cm²!
Practice Test
It is now time for you to show your understanding!
1. Find the cube’s surface area if its sides are 6 cm long.
2. Calculate the rectangular prism’s surface area with a length of 4 cm, width of 2 cm, and height of 3 cm.
3. A cylinder has a height of 8 cm and a radius of 3 cm. What is its surface area? Use π = 3.14.
4. Calculate the surface area of a sphere with a radius of 5 cm. Use π = 3.14.
5. Find the surface area of a cone with a slant height of 5 cm and a radius of 3 cm? Use π = 3.14.
Answers:
1. SA = 6s2 = 6 × 62 = 216 cm2
2. SA = 2 (lw +lh +wh) = 2 [ (4 × 2) + (4 × 3) + (2 × 3 )] = 2 [ 8 + 12 + 6 ] = 52 cm2
3. SA = 2πr2 + 2πrh = (2 × 3.14 × 32 ) + ( 2 × 3.14 × 3 × 8 ) = 56.52 + 150.72 = 207.24 cm2
4. SA = 4πr2 =4 × 3.14 × 52 = 314 cm2
5. SA = πr2 + πrs = (3.14 × 32) + (3.14 × 3 × 5 ) = 28.26 + 47.1 = 75.36 cm2
Frequently Asked Questions (FAQs)
Why do we need to learn about surface area?
The concept of the surface area is used in many real-life situations, like painting a room, buying the appropriate amount of fabric to make a dress, or even wrapping a gift!
What is the formula for a cube’s surface area?
The formula for a cube’s surface area is 6s², where s is the length of a side of the cube.
What is the difference between area and surface area?
The region inside the perimeter of a flat object, like a square or a rectangle, is referred to as the area. The surface area is the entire area of a three-dimensional object’s faces or surfaces.
Is the surface area always measured in square units?
Like all areas, the surface area is always measured in square units.
Recommended Worksheets
Surface Area of a Prism (International Museum Day themed) Math Worksheets
Surface Area of a Pyramid (Winter Solstice Themed) Math Worksheets
Surface Area of a Sphere (Songkran Festival Themed) Math Worksheets









