Introduction
Tangrams are an engaging and creative way to teach and learn mathematics. They are an ancient Chinese puzzle consisting of seven flat pieces called tans, which can be rearranged to form various shapes. In this article, we shall examine the world of tangrams and how they may be used to understand arithmetic. We will cover grade appropriateness, math domain, common core standards, definition, key concepts, illustrative examples, real-life applications, practice tests, and FAQs related to tangrams.
Grade Appropriateness
Tangrams can be used in a variety of grade levels, starting as early as kindergarten and extending through middle school. They are particularly useful for introducing younger students to geometry, spatial reasoning, and problem-solving, while older students can benefit from their applications in more complex math problems.
Math Domain
Tangrams are primarily used in the domain of Geometry, focusing on topics such as shapes, symmetry, and spatial reasoning. They can also be used to introduce concepts in Fractions and Measurement.
Applicable Common Core Standards
The use of tangrams aligns with the following Common Core Standards:
K.G.A.1: Describe objects in the environment using names of shapes and describe the relative positions of these objects.
K.G.A.2: Correctly name shapes regardless of their orientations or overall size.
1.G.A.1: Distinguish between defining attributes (e.g., triangles are closed and three-sided) versus non-defining attributes (e.g., color, orientation, overall size).
3.G.A.1: Understand that shapes in different categories may share attributes and that the shared attributes can define a larger category.
Definition of Tangram
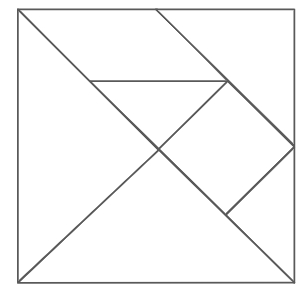
A tangram is a dissection puzzle comprising seven flat pieces called tans. The tans are typically cut from a square and include five triangles (two large, one medium, and two small), one square, and one parallelogram. The puzzle aims to rearrange the tans to form a specific shape, using all the pieces without overlaps or gaps.
The figure below shows a seven-piece tangram.
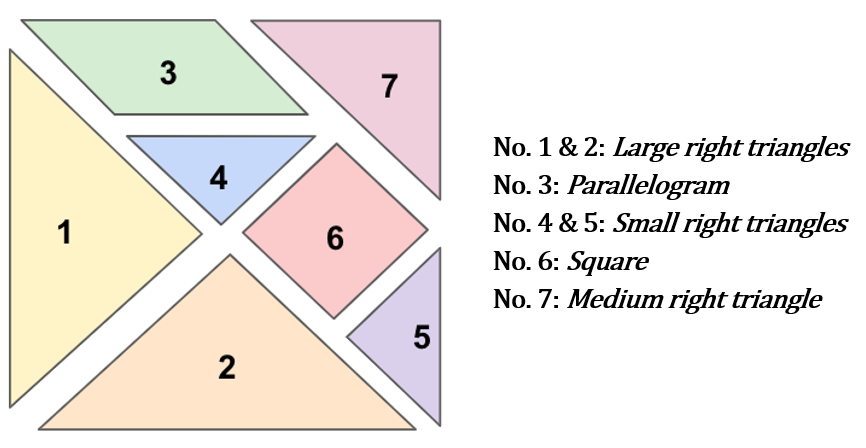
The triangles in a tangram are all right isosceles triangles, but their sizes vary. The angles in these triangles are 45°, 45°, and 90°, and the legs are the same length. The colors green, red, blue, and yellow are usually used to paint each tangram set. The tans may be made from different materials like plastic, wood, or stone.
Key Concepts
Spatial reasoning: Tangrams help develop spatial reasoning skills by requiring students to visualize and manipulate shapes to fit together.
Problem-solving: Tangrams encourage creative problem-solving as students experiment with different arrangements to achieve the desired shape.
Geometry: Tangrams can be used to teach concepts such as shape recognition, symmetry, area, and perimeter.
Discussion with Illustrative Examples
Example 1
Students can be asked to create a square using all seven pieces using a tangram set. This exercise helps students develop spatial reasoning and problem-solving skills.
Example 2
Students can be tasked with creating various shapes, such as a rectangle, a triangle, or an animal, using the tangram pieces. This activity promotes shape recognition and understanding of geometric concepts.
Examples with Solution
Example 3
Using tangram pieces, create a parallelogram with a height of 2 units and a base of 4.
Solution
Arrange the pieces of the tangram to create the desired parallelogram.
Real-life Application with Solution
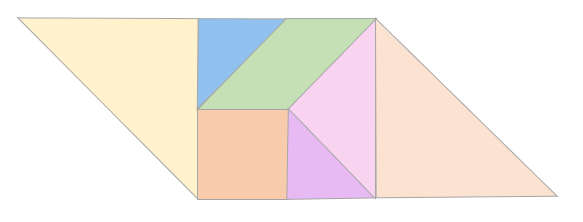
Mr. Gary plans to plant his crops to look like a tangram puzzle. Below is the layout of the crop arrangement for the seven crops.
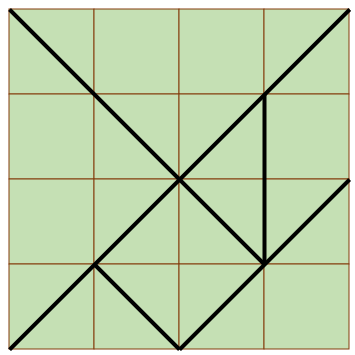
If each side of the square lot measures 20 meters, find the area of the following:
a. small triangle
b. large triangle
c. parallelogram
Solution
Since each side of the entire square lot measures 20 meters, we can calculate that the area of each small square is 5 m×5 m=25m2.
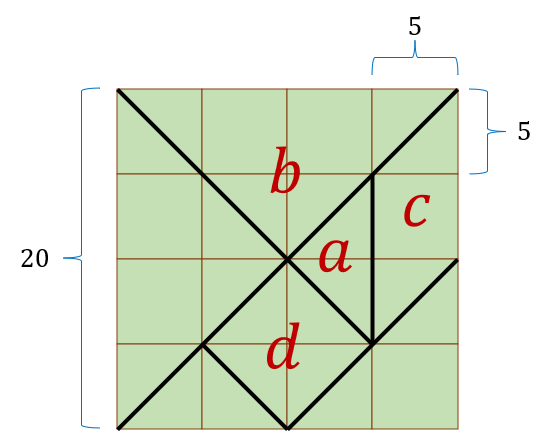
a. The area of the small triangle is equivalent to that of a small square; hence its area is 25 m2.
b. The area of the large triangle is equivalent to the area of four small squares, so its area is 4×25 m2, equal to 100 m2.
c. . The area of the parallelogram is equivalent to the area of 2 small squares, so its area is 2×25 m2, equal to 50 m2.
Practice Test
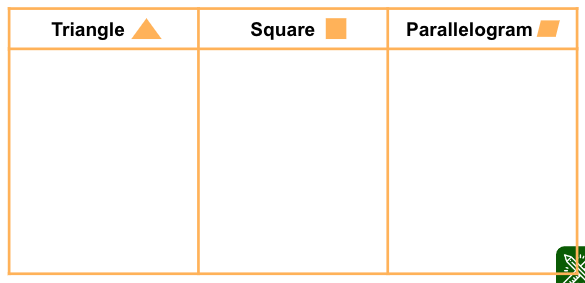
Sort the numbered tangram pieces (tans) below by their shapes. Write the number of the tans under their corresponding shape column.
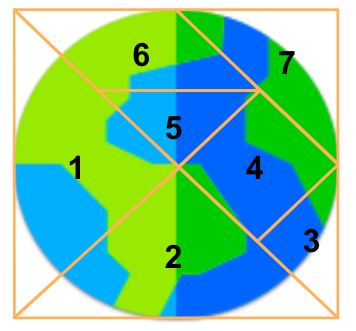
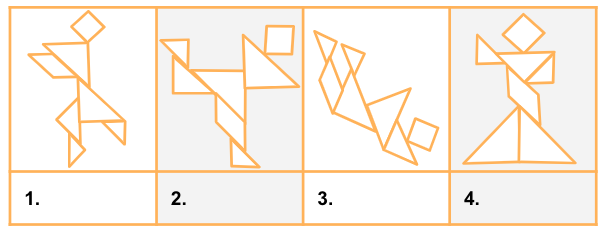
Match the festival dancers to the tangram puzzles that best resemble their position. In the spaces provided for each number, write the letter of your response.

Frequently Asked Questions (FAQs)
What are tangrams?
Tangrams are Chinese geometric puzzles made of a square and split into seven parts, called tans, that can be assembled to form various other shapes. It is made up of five triangles (two small right triangles, one medium right triangle, and two large right triangles), a square, and a parallelogram.
How many pieces are in a traditional tangram set?
A traditional tangram set has seven parts called tans.
How many triangles are there in a set of tangrams?
There is a total of five triangles in a tangram set.
two small right triangles
one medium right triangle
two large right triangles
Why do we use tangrams?
Tangrams may promote creativity, perceptual reasoning, visual-spatial awareness, problem-solving skills, and various mathematical principles, including congruency, symmetry, area, geometry, and perimeter. They help in the acquisition of geometric vocabulary and the improvement of students’ problem-solving skills.
How to create tangrams?
When creating tangrams, here are a few things to take note of:
Tangram puzzles require the usage of all seven parts.
All its seven parts must connect.
The figures created must be flat.
The tans should not overlap.
You may also rotate or flip the tans.
Below is an example of a seven-piece tangram set. We can cut these pieces by putting them together in different ways to make different shapes and objects.
There are a variety of tangram figures and shapes that can be created. Some common themes are animals, modes of transportation, and everyday inanimate objects.
Here are some examples of tangram puzzles:

Recommended Worksheets
Types of Triangles (World Animal Day Themed) Math Worksheets
Abstract Thinking Skill: Tangrams (Winter Solstice Themed) Math Worksheets
Area of a Parallelogram (Earth Day Themed) Math Worksheets









