What is a 2-dimensional geometric shape?
A shape with length and width but no depth Is called a two-dimensional shape. In a nutshell, all 2-dimensional shapes are flat and cannot be physically held. Geometric shapes are mathematical models from real-world objects with similar geometric properties.
The image below shows some of the 2-dimensional shapes we use in geometry.
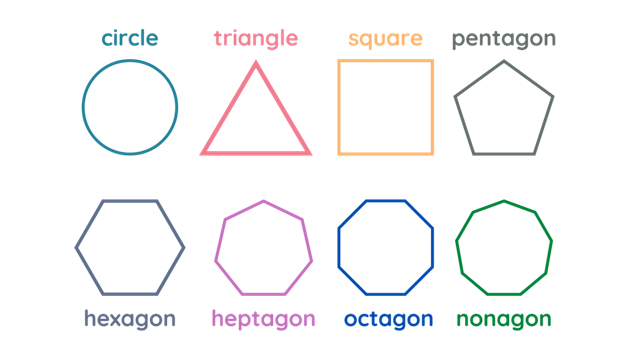
What are the different types of 2-dimensional geometric shapes?
We can classify a 2-dimensional shape depending on the number of sides, how it is formed, and by its lengths and widths.
Circle
A circle is a closed 2D shape whose points are always the same distance from the central point. A circle is made out of a curved line. Hence, it does not have sides or edges.
Students sometimes confuse a circle as a polygon. However, a circle is not a polygon, and will not be a polygon since a circle is formed by a single curved line and not from line segments. Thus, it does not meet the criteria for being a polygon.
Polygon
A polygon is a closed and flat figure on a plane with straight sides. It is made of line segments wherein each of which intersects with exactly two other line segments. Polygons are named and determined based on the number of sides, such as triangles, quadrilaterals, pentagon, hexagon, etc.
How can we classify a 2-dimensional geometric shape?
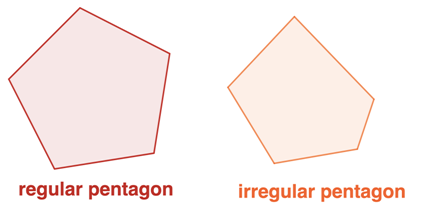
We can classify a 2D shape as a regular and irregular shape. When classifying a 2D shape, we need to consider the measure of the lengths of each side and its interior angles.
Regular shapes
If all of the sides of a 2D object have the same length and all interior angles are the same, it is said to be regular.
Irregular shapes
If all of the sides of a 2D object are of unequal length and all angles are of unequal measure, it is considered irregular.
The image below shows how a regular 2D shape differs from an irregular 2D shape.
What are the properties of 2-dimensional geometric shapes?
2-dimensional shapes cannot be held physically, but they can be drawn on a sheet of paper. We can see different objects around us that resemble a circle, triangle, square, rectangle, etc. Let’s dive deeper into distinguishing the characteristics and properties of a 2-dimensional geometric shape.
Circle
A circle does not have a length and width. However, we still consider it as a 2-dimensional shape because it does not have depth.
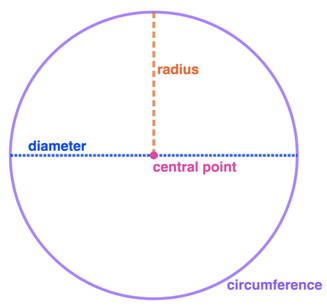
We can say that a 2-dimensional shape is a circle if it a closed, completely rounded shape.
The parts of a circle are the central point, radius, diameter, and circumference.
- The central point is the point located at the center of a circle.
- The distance around a circle can be defined as its circumference. Assume a string with a length of 15 cm, which is bent to form a circle. The circumference is equal to the length of the wire, which in this case, is 15 cm.
- The radius is the distance from the center of the circle to any point on the circumference.
- The diameter of a circle is the longest possible line segment that can be drawn in a circle. It is a line segment that runs across the circle through its center. The measure of a diameter is twice the measure of a radius.
- All circles have 360 degrees of angle measure.
Polygon
The properties and kinds of polygons differ depending on the number of sides it has. Some common types of polygons are triangle, square, rectangle, pentagon, hexagon, etc. Let’s take a look at some of the polygons and define their characteristics.
Triangle
A triangle is a closed, two-dimensional shape with three straight sides. A triangle is formed when three straight lines meet. Every triangle has three sides, three vertices, and three angles.
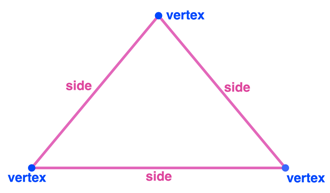
Any 3-sided polygon is called a triangle. The name of the parts of a triangle differs depending on the kind of triangle you have. In general, we call them as sides and vertex.
- The sides of a triangle are the distance of a line segment from one vertex to another.
- The vertex is the point where two sides meet.
- The sum of the three interior angles of any triangle is 180°.
Triangles can be classified in two ways – according to their angles or sides. The image below shows some of the samples of triangles.

- An equilateral triangle is a triangle where all sides and all angles are equal. Hence, the measure of the three interior angles is 60°.
- A right triangle is a triangle where one angle measures exactly 90°.
- A scalene triangle is a triangle where all three sides have a different measure. Since all sides are of different lengths, the angle measures of the three angles are also different.
Quadrilaterals
A quadrilateral is a polygon that has exactly four sides. The sum of the interior angles of a quadrilateral is 360°. There are different kinds of quadrilateral such as square, rectangle, rhombus, and kite. Quadrilaterals can be classified by their sides, angles, diagonals, and vertices.
Square – it is a 2D quadrilateral having all sides equal in length, and each angle is a right angle.
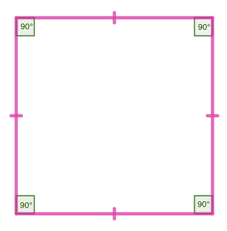
- All four sides of a square are equal.
- The opposite sides of a square are both parallel.
- All interior angle of a square are equal and measures 90°.
Rectangle – it is a 2D quadrilateral where the opposite sides are parallel and equal.
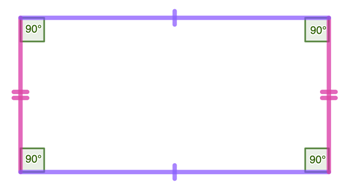
- All interior angles of a rectangle measure exactly 90°.
- The opposite sides are equal.
- The opposite sides are parallel to each other.
The image below shows more samples of a quadrilateral.
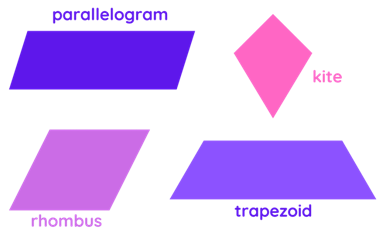
- A parallelogram is a quadrilateral where both pairs of opposite sides are parallel and equal. The special cases of a parallelogram are square, rectangle, rhombus, and rhomboid.
- A trapezoid is a quadrilateral geometric shape where it only has one pair of parallel sides. The parallel sides of a trapezoid are called as the bases, and the other two sides are called the legs.
- A rhombus is a quadrilateral where four sides are of equal measures, and the pair of opposite sides are parallel to each other. The interior angle of a rhombus is not 90°.
- A kite is a quadrilateral where two pairs of adjacent sides are congruent.
Pentagon
A pentagon is a 2D closed polygon with five sides and five interior angles. The sum of the interior angle of any pentagon is 540°. Pentagons can be classified as either a regular pentagon or an irregular pentagon.
Regular Pentagon – is a five-sided polygon where all sides and interior angles are equal.
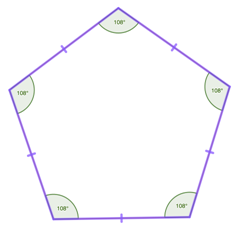
- All sides of a regular pentagon are equal in length.
- All interior angle of a regular pentagon measures 108°.
- All exterior angle of a regular pentagon measures 72°.
Irregular pentagon – it is a five-shaped 2D polygon where all sides and angles are of different measure.
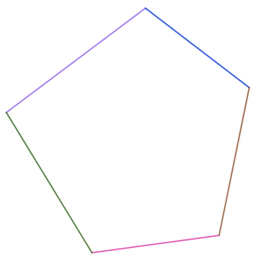
- All five sides of an irregular pentagon have different length measures.
- All five interior angles are not equal.
Pentagons can also be classified depending on whether if the vertices are pointing outwards or inwards. Let’s take a look at the image of a convex and concave pentagon.
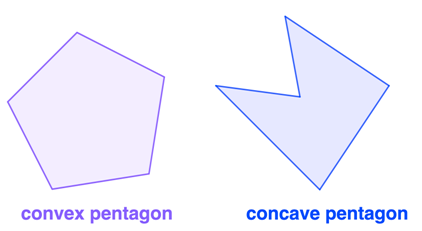
- A convex pentagon is a pentagon where all fives vertices are pointing outwards.
- A pentagon is said to be a concave pentagon if at least one of the vertex is pointing inwards.
The table below shows more kinds of regular and irregular polygons.
| NAME | NUMBER OF SIDES | |
| Hexagon | 6 | 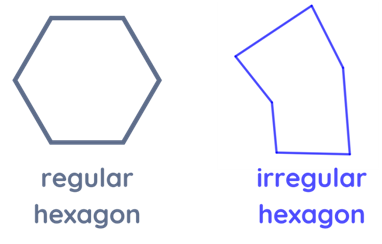 The sum of all interior angles of a hexagon is 720°. A regular hexagon is a six-sided polygon where all sides and interior angles are equal. The measure of each of the interior angles of a regular hexagon is 120°. On the other hand, the irregular hexagon does not have equal sides and angles. |
| Heptagon | 7 | 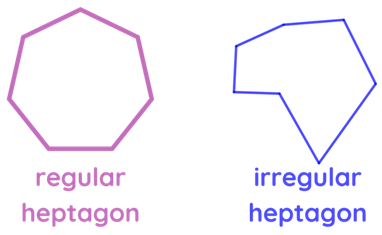 The sum of all interior angles of a heptagon is 900°. It is said to be a regular heptagon if all seven sides and seven angle measures are equal. Irregular hexagon does not have equal sides and angles. |
| Octagon | 8 | 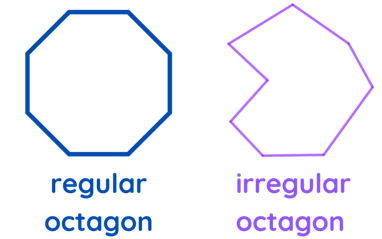 An octagon is an 8-sided polygon where the sum of all the interior angles is 1080°. In a regular octagon, all sides are equal and each interior angle measures exactly 135°. If the sides and angle measure of an eight-sided polygon is not equal, it is called an irregular octagon. |
| Nonagon | 9 | 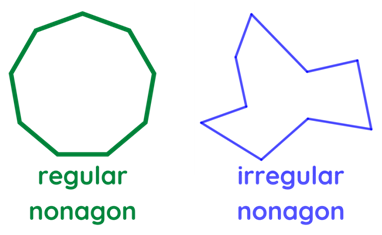 A nonagon is a 9-sided polygon where the sum of the interior angle is 1260°. If all sides and interior angles of a nonagon are all equal, then it is a regular nonagon. The measure of each interior angle of a regular nonagon is 140°. If the sides and interior angles are not equal, then it is an irregular nonagon. |
| Decagon | 10 | 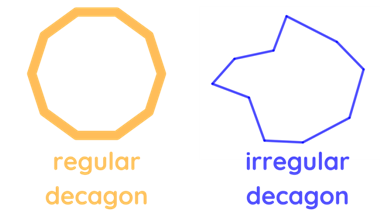 A decagon is a 10-sided polygon where the sum of all its interior angles is equal to 1440°. In a regular decagon, all sides are equal and the measure of each interior angle is 144°. Meanwhile, an irregular decagon is a 10-sided polygon where no sides and no interior angle are equal. |
What are the real-life samples of 2-dimensional geometric shapes?
2-dimensional geometric shapes are used to model real-world objects. Students sometimes consider a sheet of paper or plastic as a 2-dimensional shape when it is not. Even though the depth of a sheet of paper is thin, it is a 3-dimensional object.
Let’s take a look at some examples of a 2-dimensional shape in real-world objects.
| 2-dimensional geometric shape | Real-world object |
| Circle |  Some real-world objects that look like a circle are hula hoops, wheels, rings, fans, clocks, etc. Additionally, whenever we draw a sun or a planet, we also use a circle to represent it. |
| Triangle | 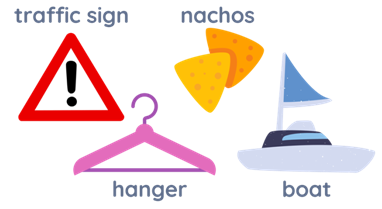 We can almost see a triangle everywhere, such as a traffic sign, nacho chips, a hanger, and a sailboat’s mainsail (flag). There is also an instrument that is named as a triangle because it resembles a triangle. More so, triangles are sometimes used in creating pyramids, bridges, and buildings. |
| Square |  Some real-world objects that resemble a square are chessboards, a slice of cheese, and a sandwich. |
| Rectangle |  Just like a triangle, many things around us resemble a rectangle. Most of the tabletops are created in the shape of a rectangle. Some other examples of a rectangle are the screens of a laptop, a book, a sheet of paper. Even the walls, doors, and windows in our house resemble a rectangle. |
What is the difference between a 2D shape and a 3D object?
As the name suggests, 2D and 3D shapes differ on the number of dimensions they have. A 2-dimensional shape has the dimensions of length and width, while a 3-dimensional is a solid shape having the dimensions of length, width, and depth (or height).
Let’s look at the table below to compare the characteristic of a 2D and 3D shape.
| 2-Dimensional Shape | 3-Dimensional Shape | |
| Definition | A 2-dimensional shape is a flat shape that has only two dimensions – length and width. A 2-dimensional shape cannot be physically held. | A 3-dimensional shape is a solid shape that has three dimensions – length, width, and depth (height). |
| Dimensions | length x width | length x width x height |
| Mathematical axes | x-axis and y-axis | x-axis, y-axis, and z-axis |
| We can only calculate the area and perimeter of a 2D shape. | In any 3-dimensional object, we can compute for the surface area, lateral area, cross-sectional area, and volume. | |
| Examples | Circle, triangle, square, rectangle, parallelogram, trapezoid, pentagon, hexagon, heptagon, etc. | Sphere, triangular prism, cube, rectangular prism, pyramid, cylinder, cone, etc. |
What is the importance of 2-dimensional geometric shapes?
Aside from practicing our child to draw circles, triangle, or squares in a sheet of paper, most children experienced playing with toys with different shapes. At an early age, children already perceive various shapes even if they are unaware of their names. The specific qualities of each shape, such as the number of sides or angle measures, are taught when they reach elementary school.
During preschool, children practice a lot with shapes that help them solidify their understanding and concept of two-dimensional figures. One example exercise is shape arranging. When a child grasps the characteristics of a shape, say, for example, a rectangle – they can easily match them to the rectangle gap on the toy.
More so, the ability to recognize and identify 2D shapes is essential for future math learning. Preschool students can improve their perception of numbers and what they appear like if they have a strong understanding of shapes. Number recognition is a fundamental arithmetic skill that kids must master.
Students may have difficulty in understanding geometry and may be unable to recognize 3D shapes. Identifying the kind of 2-dimensional shape will help you determine what formula to use in getting the perimeter or area of a certain shape. Hence, it is essential to identify 2D shapes in solving geometric problems and getting its measures.
Recommended Worksheets
Understanding Congruence and Similarity of 2D Figures 8th Grade Math Worksheets
Understanding the properties of rotations, reflections, and translations of 2D figures 8th Grade Math Worksheets
Drawing And Describing 2D And 3D Figures 7th Grade Math Worksheets









