Introduction
A line, line segment, and ray are all referred to as one-dimensional figures as they only have length.
A line extends endlessly in two directions and has no beginning or end. In a line, rays are included. It stretches endlessly in one direction and has a single endpoint. Another part of a line is a line segment (or simply segment). It is the only one of these concepts that have a measurement or length and has two endpoints.
We will learn more about line segments, rays, and lines in this topic. To better distinguish the three figures, we shall talk about their properties.
Line Segment
A fixed section of a line is called a line segment. A line segment has two endpoints, which are used to name it.
For example, in the figure below, we have two points, X and Y. The section of the line from point X to point Y is line segment XY. The name of a line segment is given using capital letters. This line segment is denoted as $\overline{XY}$.

A line segment’s length can be measured. It has a finite length because of its defined two endpoints. Real-life examples of line segments are the edges of a table, the perimeter of a sports field, and the pasta noodles for your spaghetti cravings. Line segments are also used by professionals in doing their drafts of architectural designs.
Ray
A geometrical ray is a portion of a line that originates from a fixed point and extends in any direction away from the starting point. The starting point is also called the point of origin.
For example, the figure below shows that it starts from point X and point Y is near the arrow end. Ray XY is the segment that runs from point X through point Y and then extends. The name of a ray is given using capital letters; hence, it is denoted as ray $\underset{XY}{\rightarrow}$.
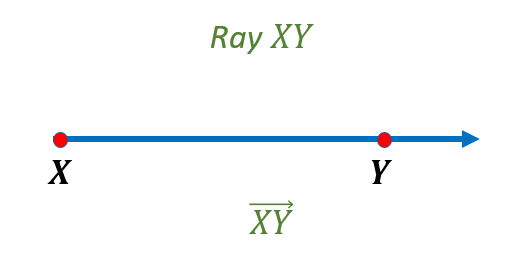
The indeterminate length of a ray prevents measurement of it. The endpoint serves as the beginning point for rays; however, measuring a ray is not possible without a second endpoint since the other end moves infinitely.
Rays in nature include the sun’s light. The sun, which acts as the ray’s point of origin, is the source of light. Another illustration is the light coming from a flashlight, which extends as far as light can go from the end of the flashlight.
Line
A line is made up of an unlimited number of points that stretch in two opposing directions. In geometry, when we draw a line, we use arrows at each end to show that it extends infinitely to the opposite direction.
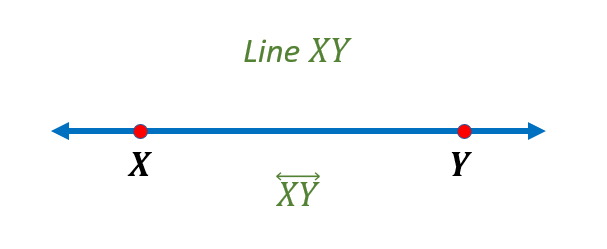
Let us say, for example, the line XY below. It has points X and Y, and the arrowheads at each end indicate that it extends infinitely. A line is labeled using two capital letters. Hence, the line below is denoted as $\underset{XY}{\leftrightarrow}$.
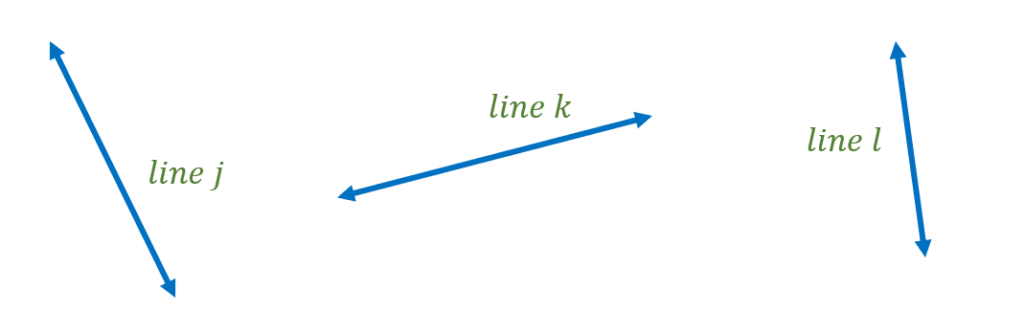
A line can also be named using a lowercase letter. For example, the figure below shows lines a, b, and c.

There can be multiple lines that pass through a point, but there can only be one line that passes through any two points.

Types of Lines
The basic lines in geometry are horizontal, vertical, parallel, perpendicular, and intersecting.
A line is considered to be horizontal when it moves straight from left to right. Horizontal lines are parallel to the x – axis in a coordinate system and perpendicular to the y – axis. The image below shows a horizontal line.

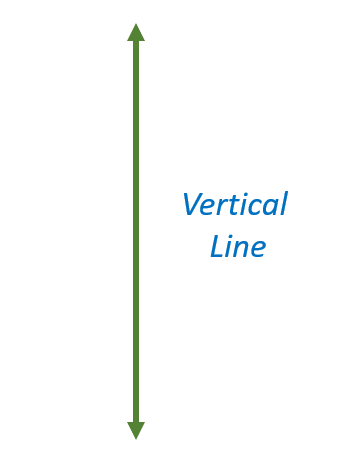
A line is vertical when it moves straight from top to bottom. Vertical lines are parallel to the y – axis in a coordinate system and perpendicular to the x – axis. The image below shows a vertical line.
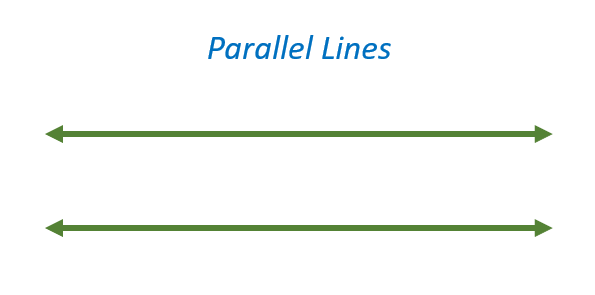
Two straight lines are parallel when they do not cross or intersect at any point, not even at infinity. In terms of geometry, parallel lines are two separate lines that never cross each other and are located in the same plane. The image below shows two parallel lines.
In geometry, two lines are perpendicular to one another when they meet or intersect at a 90-degree angle. The image below shows two lines that are perpendicular.

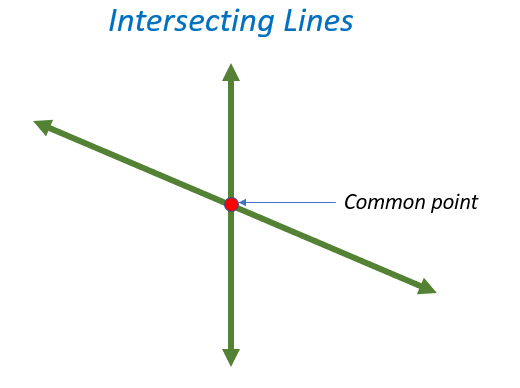
In a plane, intersecting lines are any two or more lines that cross one another. A common point that is shared by all the crossing lines can be found there. The image below shows two intersecting lines.
Properties of Line Segment, Ray, and Line
The properties of a line segment, ray, and line are displayed in the table below.
| Properties | Line | Line Segment | Ray |
| Endpoints | A line has no endpoints. | A line segment has two endpoints. | A ray has one starting point and another point near the arrowhead. |
| Length | A line’s length cannot be measured. | A line segment’s length is measurable. | A ray’s length cannot be measured. |
| Symbol | The symbol of a line is ↔. | The symbol of a line segment is -. | The symbol of a ray is →. |
Drawing Line Segment, Ray, and Line
The following gives an example of how to draw a line segment, ray, and line.
Drawing a line segment
To create a line segment, join the two endpoints with a straight edge.
Let us say, for example, we have the endpoints F and G, as shown below. We must connect the two endpoints with a straight edge to create a line segment.

The name of a line segment is given using capital letters. This line segment is denoted as $\overline{FG}$.
Drawing a ray
To draw a ray, draw a line segment starting with the endpoint and ending with an arrow rather than another endpoint. The arrow indicates that the ray never ends.
Let us say, for example; we have the endpoints A and B below. To draw a ray, we must connect these endpoints forming a line segment, then extend the straight edge and end with an arrow.
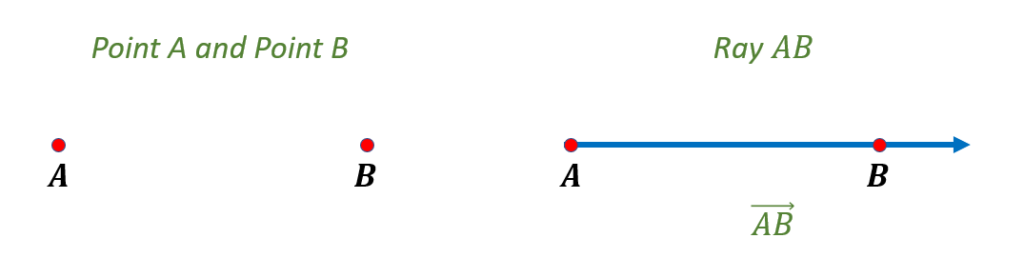
The name of a ray is given using capital letters; hence, it is denoted as ray $\underset{AB}{\rightarrow}$.
Drawing a line
To draw a line, create a straight edge connecting the two points and ends with arrows. The arrows indicate that the line extends in the opposite direction infinitely.
Let us say, for example; we have points J and K below. To draw a line that includes these points, we must connect them using a straight edge and end with arrows on both ends.

A line is labeled using two capital letters; hence, the line above is denoted as $\underset{JK}{\leftrightarrow}$.
Note that lines can also be named using lowercase letters. For example, as shown below, we have lines j, k, and l.
Naming Lines, Rays, and Line Segments
Naming Lines
A line is continuous in both directions and has no end. Arrow tips are added at both ends, or any two points along the line, to signify the line’s infiniteness in both directions. Any two places along the line may be used when naming the line. Then, over the two letters, we add a bidirectional arrow. The symbol of a line is . Examples are $\underset{JK}{\leftrightarrow}$, $\underset{MN}{\leftrightarrow}$, $\underset{OR}{\leftrightarrow}$, $\underset{TU}{\leftrightarrow}$, and $\underset{CD}{\leftrightarrow}$.
Naming Rays
A ray typically includes an arrow tip at the end to indicate that it is limitless. When we give a ray a name, we first write the letter representing the endpoint, followed by the letter representing any one point along the ray. Then, over the two letters, we add a single arrow.
Naming Line Segments
Segments are the parts of a line that have two endpoints. We use a line over the two letters that stand in for the two endpoints when naming a line segment. The symbol of a line segment is -. Examples are $\overline{ST}$, $\overline{BC}$, $\overline{EF}$, $\overline{UV}$, and $\overline{GH}$.
Examples
Example 1
Do the line segments GH and KL will meet anywhere?

Solution
No. The line segments $\overline{GH}$ and $\overline{KL}$ will not meet anywhere. Note that these are line segments, and they have their endpoints. The illustration above shows that these line segments are parallel to each other, and thus, they will never meet.
Example 2
Do the lines MN and ST will meet anywhere?
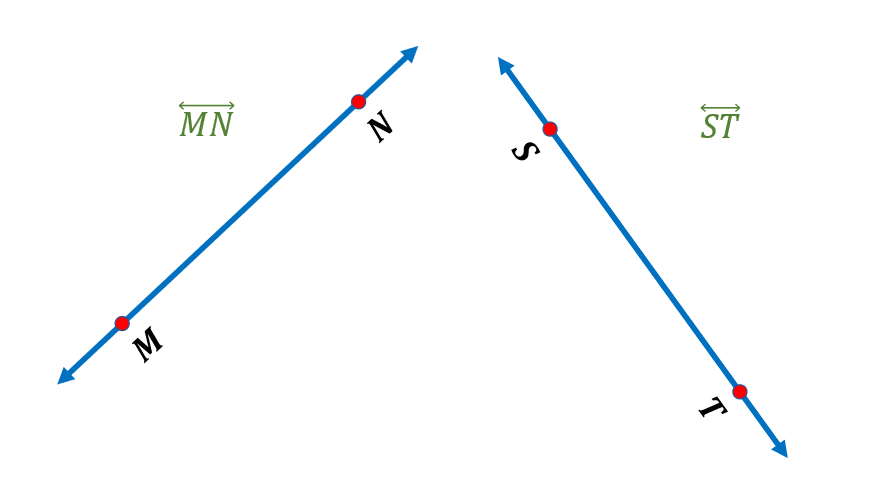
Solution
The two lines will meet at some point at their intersection. Remember that a line extends infinitely towards the opposite directions; therefore, line MN and line ST will meet at some point when extended.
Example 3
Determine which are rays, lines, or line segments.
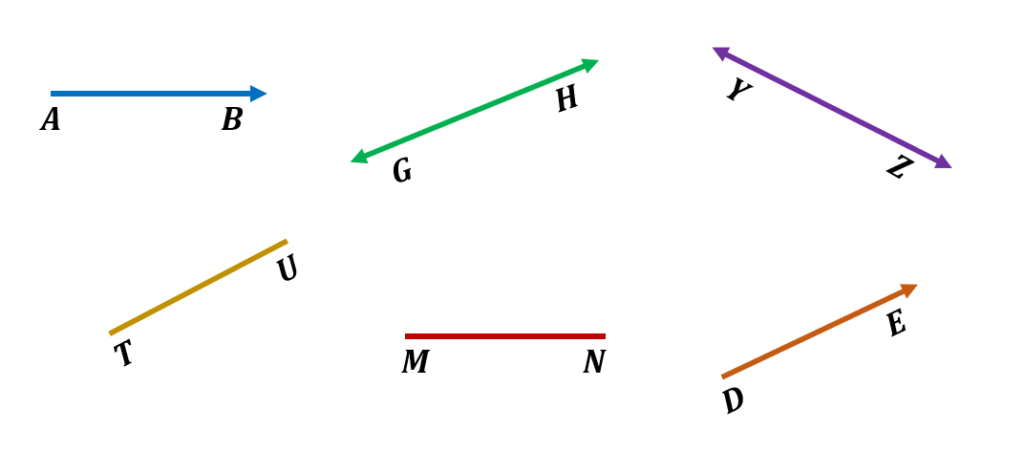
Solution
Remember that a line is a continuous, straight path that has no endpoints and travels in both directions along a plane. A line segment is a finitely long portion of a line with two endpoints. A ray has an endpoint and keeps extending in one direction.
Therefore, in the given illustration, the lines are $\underset{GH}{\leftrightarrow}$and $\underset{YZ}{\leftrightarrow}$. Notice that these figures have arrowheads at both ends.
The line segments are $\overline{TU}$ and $\overline{MN}$. Notice that these figures have their endpoints and no arrowheads.
The rays are $\underset{AB}{\rightarrow}$ and $\underset{DE}{\rightarrow}$. These figures have starting points and arrowheads at the other end.
Example 4
Give five instances of rays, lines, and line segments.
Solution
The name of a line segment is given using capital letters. The symbol of a line segment is -. Examples are $\overline{ST}$, $\overline{BC}$, $\overline{EF}$, $\overline{UV}$, and $\overline{GH}$.
The name of a ray is given using capital letters. The symbol of a ray is →. Examples are $\underset{HI}{\rightarrow}$, $\underset{LM}{\rightarrow}$, $\underset{WX}{\rightarrow}$, $\underset{AB}{\rightarrow}$, and \underset{FG}{\rightarrow}.
A line is labeled using two capital letters. The symbol of a line is . Examples are $\underset{JK}{\leftrightarrow}$, $\underset{MN}{\leftrightarrow}$, $\underset{QR}{\leftrightarrow}$, $\underset{TU}{\leftrightarrow}$, and $\underset{CD}{\leftrightarrow}$.
Example 5
Identify the type of lines in each item.
( a )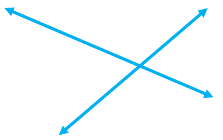 | ( c )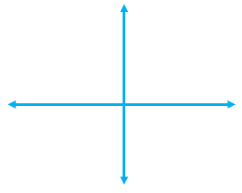 |
( b )  | ( d ) |
Solution
( a ) intersecting lines Since the two lines cross one another, they are intersecting lines. It can also be seen from the image that they have a common point. | ( c ) perpendicular lines Since the two lines meet or cross at a 90-degree angle, they are perpendicular to one another. |
( b ) parallel lines The lines are parallel since they do not cross or intersect at any point, not even at infinity. In terms of geometry, parallel lines are two separate lines that never cross each other and are located in the same plane. The image below shows two parallel lines. | ( d ) horizontal lines The line is horizontal since it moves straight from left to right or vice versa. |
Summary
A fixed section of a line is called a line segment. A line segment has two ends, which are used to name it. The name of a line segment is given using capital letters. The symbol of a line segment is -. Examples are $\overline{ST}$, $\overline{BC}$, $\overline{EF}$, $\overline{UV}$, and $\overline{GH}$..
A geometrical ray is a portion of a line that originates from a fixed point and extends in any direction away from the starting point. The name of a ray is given using capital letters. The symbol of a ray is →. Examples are $\underset{HI}{\rightarrow}$, $\underset{LM}{\rightarrow}$, $\underset{WX}{\rightarrow}$, $\underset{AB}{\rightarrow}$, and \underset{FG}{\rightarrow}.
A line is made up of an unlimited number of points that stretch in two opposing directions. In geometry, when we draw a line, we use arrows at each end to show that it extends infinitely to the opposite direction. A line is labeled using two capital letters. The symbol of a line is . Examples are $\underset{JK}{\leftrightarrow}$, $\underset{MN}{\leftrightarrow}$, $\underset{QR}{\leftrightarrow}$, $\underset{TU}{\leftrightarrow}$, and $\underset{CD}{\leftrightarrow}$.
The basic lines in geometry are horizontal, vertical, parallel, perpendicular, and intersecting. A line is horizontal when it moves straight from left to right. A line is vertical when it moves straight from top to bottom. Two straight lines are parallel when they do not cross or intersect at any point, not even at infinity. Two lines are perpendicular to one another when they meet or intersect at a 90-degree angle. Intersecting lines are any two or more lines that cross one another. A common point that is shared by all the crossing lines can be found there.
The properties of a line segment, ray, and line are displayed in the table below.
| Properties | Line | Line Segment | Ray |
| Endpoints | A line has no endpoints. | A line segment has two endpoints. | A ray has one starting point and another point near the arrowhead. |
| Length | A line’s length cannot be measured. | A line segment’s length is measurable. | A ray’s length cannot be measured. |
| Symbol | The symbol of a line is ↔. | The symbol of a line segment is -. | The symbol of a ray is →. |
Frequently Asked Questions about Line-Segment, Ray, and Line Geometry ( FAQs )
What is a line in geometry?
A line is a continuous, straight path that has no endpoints and travels in both directions along a plane. In geometry, when we draw a line, we use arrows at each end to show that it extends infinitely to the opposite direction. A line is labeled using two capital letters. The symbol of a line is . Examples are $\underset{JK}{\leftrightarrow}$, $\underset{MN}{\leftrightarrow}$, $\underset{QR}{\leftrightarrow}$, $\underset{TU}{\leftrightarrow}$, and $\underset{CD}{\leftrightarrow}$.
What is a ray in geometry?
A ray has an endpoint and keeps extending in one direction. In geometry, when we draw a line, we use arrows at each end to show that it extends infinitely to the opposite direction. A line is labeled using two capital letters. The symbol of a line is . Examples are $\underset{JK}{\leftrightarrow}$, $\underset{MN}{\leftrightarrow}$, $\underset{QR}{\leftrightarrow}$, $\underset{TU}{\leftrightarrow}$, and $\underset{CD}{\leftrightarrow}$.
What is a line segment in geometry?
A line segment is a finitely long portion of a line with two endpoints. A line segment has two ends, which are used to name it. The name of a line segment is given using capital letters. The symbol of a line segment is -. Examples are $\overline{ST}$, $\overline{BC}$, $\overline{EF}$, $\overline{UV}$, and $\overline{GH}$..
What is a ray’s point of origin?
A geometrical ray is a portion of a line that originates from a fixed point and extends in any direction away from the starting point. The starting point is also called the point of origin.
What are examples of rays in real life?
Rays in nature include the sun’s light. The sun, which acts as the ray’s point of origin, is the source of light. Another illustration is the light coming from a flashlight, which extends as far as light can go from the end of the flashlight.
Is a ray measurable?
No. The indeterminate length of a ray prevents measurement of it. The endpoint serves as the beginning point for rays; however, measuring a ray is not possible without a second endpoint since the other end moves infinitely.
What are the properties of line, line segment, and ray?
The properties of a line segment, ray, and line are displayed in the table
| Properties | Line | Line Segment | Ray |
| Endpoints | A line has no endpoints. | A line segment has two endpoints. | A ray has one starting point and another point near the arrowhead. |
| Length | A line’s length cannot be measured. | A line segment’s length is measurable. | A ray’s length cannot be measured. |
| Symbol | The symbol of a line is ↔. | The symbol of a line segment is -. | The symbol of a ray is →. |
What are real-life examples of line segments?
Real-life examples of line segments are the edges of a table, the perimeter of a sports field, and the pasta noodles for your spaghetti cravings. Line segments are also used by professionals in doing their drafts of architectural designs.
How do you draw lines, line segments, and rays?
To create a line segment, join the two endpoints together with a straight edge.
To draw a ray, draw a line segment starting with the endpoint and ending with an arrow rather than another endpoint. The arrow indicates that the ray never ends.
To draw a line, create a straight edge connecting the two points and ends with arrows. The arrows indicate that the line extends in the opposite direction infinitely.
How do we name or label lines, rays, and line segments?
Naming lines
A line is continuous in both directions and has no end. Arrow tips are added at both ends, or any two points along the line, to signify the line’s infiniteness in both directions. Any two places along the line may be used when naming the line. Then, over the two letters, we add a bidirectional arrow. The symbol of a line is . Examples are $\underset{JK}{\leftrightarrow}$, $\underset{MN}{\leftrightarrow}$, $\underset{QR}{\leftrightarrow}$, $\underset{TU}{\leftrightarrow}$, and $\underset{CD}{\leftrightarrow}$.
Naming rays
A ray typically includes an arrow tip at the end to indicate that it is limitless. When we give a ray a name, we first write the letter representing the endpoint, followed by the letter representing any one point along the ray. Then, over the two letters, we add a single arrow.
Naming line segments
Segments are the parts of a line that have two endpoints. We use a line over the two letters that stand in for the two endpoints when naming a line segment. The symbol of a line segment is -. Examples are $\overline{ST}$, $\overline{BC}$, $\overline{EF}$, $\overline{UV}$, and $\overline{GH}$..
What are the types of lines?
The basic lines in geometry are horizontal, vertical, parallel, perpendicular, and intersecting lines.
| Types of Lines | Illustration |
| A line is considered to be horizontal when it moves straight from left to right. Horizontal lines are parallel to the x – axis in a coordinate system and perpendicular to the y – axis. | |
| A line is vertical when it moves straight from top to bottom. Vertical lines are parallel to the y – axis in a coordinate system and perpendicular to the x – axis. The image below shows a vertical line. | 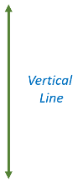 |
| Two straight lines are parallel when they do not cross or intersect at any point, not even at infinity. In terms of geometry, parallel lines are two separate lines that never cross each other and are located in the same plane. The image below shows two parallel lines. |  |
| In geometry, two lines are perpendicular to one another when they meet or intersect at a 90-degree angle. The image below shows two lines that are perpendicular. |  |
| In a plane, intersecting lines are any two or more lines that cross one another. A common point that is shared by all the crossing lines can be found there. The image below shows two intersecting lines. |  |
What differentiates a line from a line segment?
The main distinction between a line segment and a line is that a line can is extended in both directions infinitely, whereas a line segment has two endpoints.
Recommended Worksheets
Spatial Skill: Lines, Segments, and Rays (International Day of PWDs Themed) Worksheets
Parallel and Perpendicular Lines (Songkran Festival Themed) Math Worksheets
Equation of a Straight Line (National Maritime Day Themed) Math Worksheets









