What to expect in this article?
After reading this article, you will be able to add and subtract angles in a given figure or problem. You will also be able to define an angle and know the importance of adding and subtracting angles.
What is an angle?
A figure produced by two rays meeting at a common terminal point is known as an angle. An angle is denoted by the symbol and is usually measured in degrees.
Angles are sections of a full circle. A full circle can be divided into angles of many sizes. If all of the angles are placed together without overlapping, their total will be 360°. Angles can be added together to make larger angles and can also be divided into smaller angles.
How to add angles?
Two angles that are next to each other without overlapping are called adjacent angles. These angles can be added together to make a larger angle. Adding angles is the same as adding numbers. We can add two or more angles as long as they are not overlapping.
Example #1
MON and NOP are two adjacent angles. What is the total angle measure of the two angles?
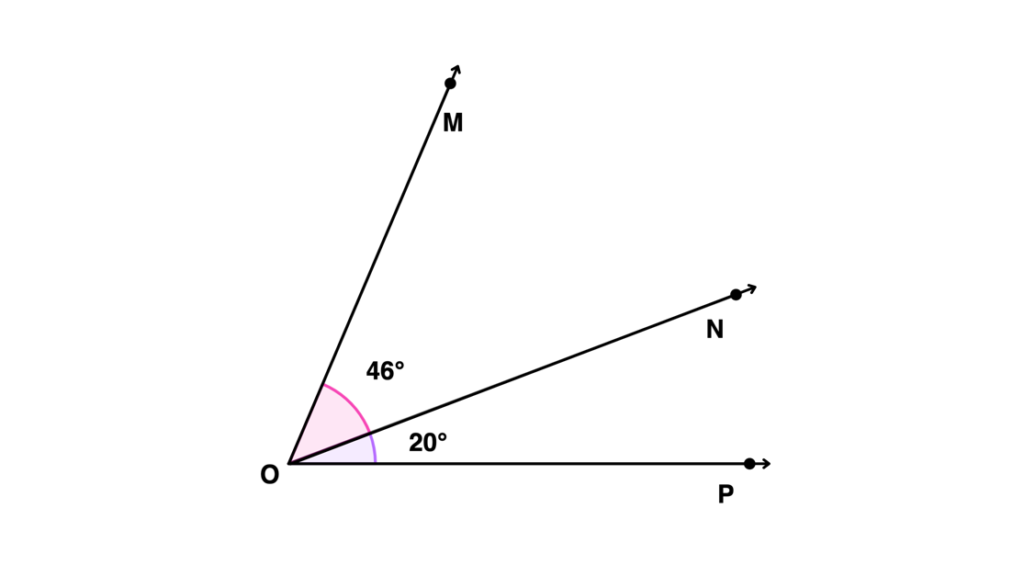
Solution
| Angle Addition Process | Step-by-step explanation |
| MON = 46° NOP = 20° | Identify the angle measure of the two angles based on the given figure. |
| MON + NOP = MOP | Add the two angles. |
| 46° + 20° = MOP | Substitute the angle measure of MON and NOP. |
| MOP = 66° | Add 46° and 20°. |
| Therefore, adding MON and NOP will result to MOP with an angle measure of 66°. |
Example #2
If BAC and CAD are two adjacent angles, determine their angle measure if we add them together.
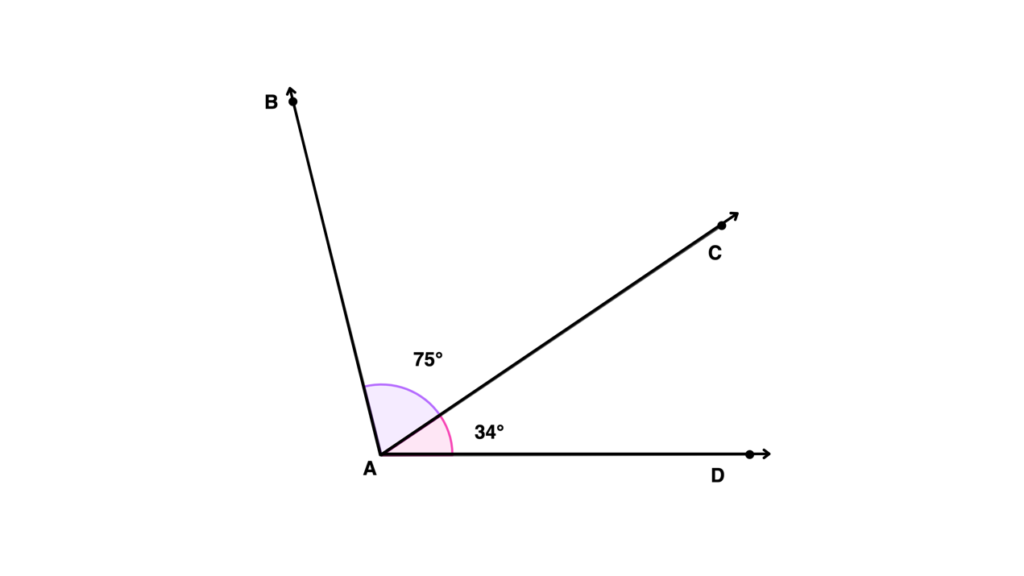
Solution
| Angle Addition Process | Step-by-step explanation |
| BAC = 75° CAD = 34° | Identify the angle measure of the two angles based on the given figure. |
| BAC + CAD = BAD | Add the two angles. |
| 75° + 34° = BAD | Substitute the angle measure of BAC and CAD. |
| BAD = 109° | Add 75° and 34°. |
| Therefore, adding BAC and CAD will result to BAD with an angle measure of 109°. |
Example #3
WXZ and ZXY are two adjacent angles. What is the sum of the two adjacent angles?
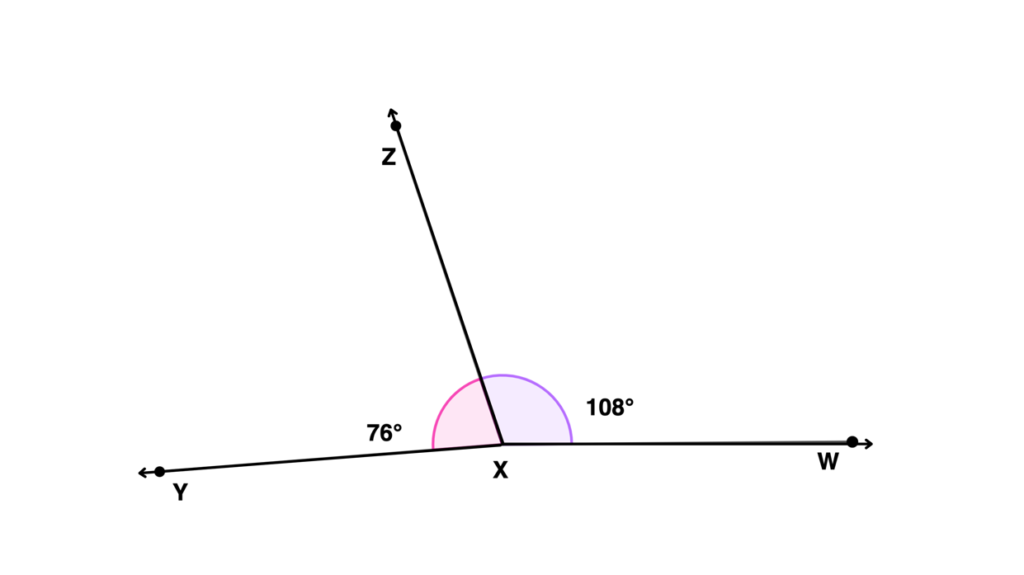
Solution
| Angle Addition Process | Step-by-step explanation |
| WXZ = 108° ZXY = 76° | Identify the angle measure of the two angles based on the given figure. |
| WXZ + ZXY = WXY | Add the two angles. |
| 108° + 76° = WXY | Substitute the angle measure of WXZ and ZXY. |
| WXY = 184° | Add 108° and 76°. |
| Therefore, adding WXZ and ZXY will result to WXY with an angle measure of 184°. |
Example #4
MJK and KJL are two adjacent angles. Find the sum of the two angles.
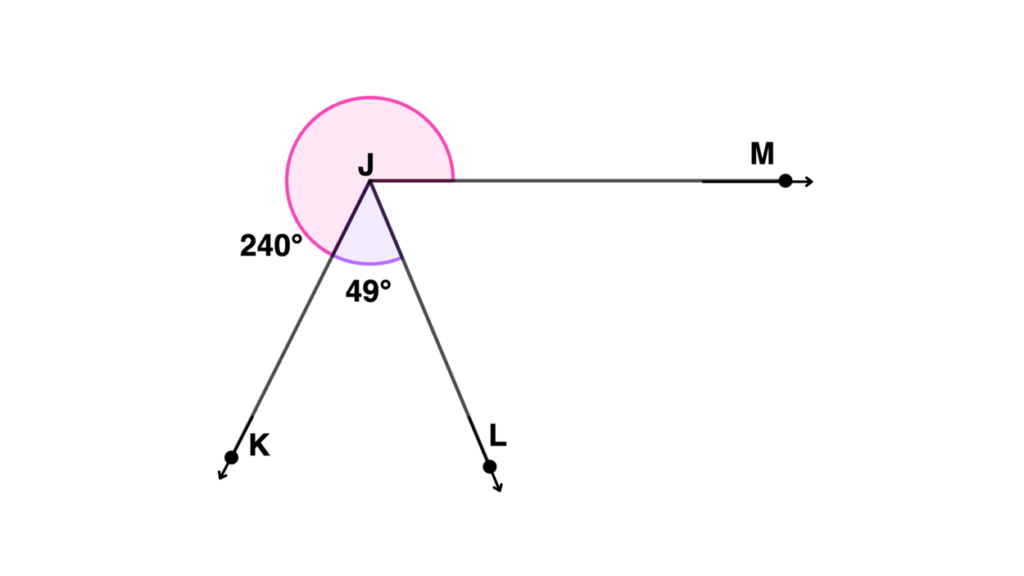
Solution
| Angle Addition Process | Step-by-step explanation |
| MJK = 240° KJL = 49° | Identify the angle measure of the two angles based on the given figure. |
| MJK + KJL = MJL | Add the two angles. |
| 240° + 49° = MJL | Substitute the angle measure of WXZ and ZXY. |
| MJL = 289° | Add 240° and 49° |
| Therefore, adding MJK and KJL will result to MJLwith an angle measure of 289°. |
How to subtract angles?
If a large angle is made up of two smaller angles, the measurement of one of the smaller angles can be subtracted from the measurement of the large angle to find the measurement of the second small angle. Just like the addition of angles, subtraction of angles is the same as simply subtracting numbers.
Example #1
If ABD measures 136°, what is the measure of ABC?
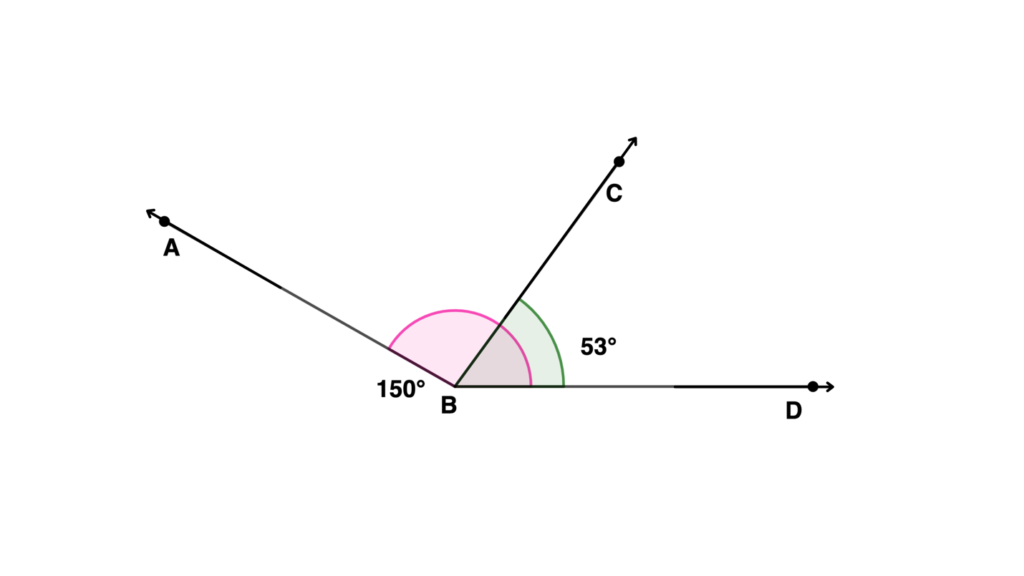
Solution
| Angle Subtraction Process | Step-by-step explanation |
| ABD = ABC + CBD | Identify what angles make up ABD based on the given figure. |
| ABD = 150° CBD = 53° | List what is already known in the figure. |
| 150° = ABC + 53° | Substitute the angle measure of ABD and CBD . |
| ABC = 150° – 53° | Set-up the subtraction process. |
| ABC = 97° | Subtract 53° from 150°. |
| Therefore, ABC measures 97°. |
Example #2
Based on the figure, if RUP measures 225°, what is the measure of QUP?

Solution
| Angle Subtraction Process | Step-by-step explanation |
| RUP = RUQ + QUP | Identify what angles make up RUP based on the given figure. |
| RUP = 225° RUQ = 67° | List what is already known in the figure. |
| 225° = 67° + QUP | Substitute the angle measure of RUP and RUQ. |
| QUP = 225° – 67° | Set-up the subtraction process. |
| QUP = 158° | Subtract 67° from 225°. |
| Therefore, QUP measures 158°. |
How to solve problems involving addition and subtraction of angles?
When solving problems involving addition and subtraction of angles, we must first be able to define what angles make up the larger angle. That way, we can avoid confusion.
Example
Angle MOP measures 126°. It is divided into two smaller angles namely, Angle MON and Angle NOP. Angle MON measures 58°, while angle NOP is unknown.
If Angle MON + Angle NOP = Angle MOP, what is the measure of Angle NOP?
Solution
| Process | Step-by-Step Explanation |
| MOP = 126° MON = 58° | If no drawing is provided in the given problem, and you need one to help you understand it, don’t be afraid to make your own visual representation. However, we will try to unpack the problem by using the information given in the problem. Pay attention to the details of the problem, and what you are being asked to solve. |
| MON + NOP = MOP | Set-up and equation that represents the problem. Since the problem says that MOP is divided into smaller angles. We can say already say that MOP has an angle measure that is greater than MON and NOP. |
| 58° + NOP = 126° | Substitute the angle measure of MOP and MON to the equation. |
| NOP = 126° – 58° | Isolate NOP. Thus, we will have NOP = 126° – 58° |
| NOP = 68° | Subtract 58° from 126°. |
What is the importance of adding and subtracting angles?
One of the significance of adding and subtracting angles is that it allows us to create larger angles. More so, it helps us prepare when it comes to the pairs of angles such as supplementary and complementary angles. Adding and subtracting angles can also help us in proving certain theorems and congruent triangles.
Recommended Worksheets
Angle Measurements (Cruise Ship Themed) Worksheets
Obtuse Angles (Winter Themed) Math Worksheets
Reflex Angles (International Artists’ Day Themed) Math Worksheets









