What is a number line?
A number line is a straight horizontal line with numbers placed at even intervals that provides a visual representation of numbers. Primary operations such as addition, subtraction, multiplication, and division can all be performed on a number line. The numbers increase as we move towards the right side of a number line while they decrease as we move left.
Browse below our Number Line generators which are available to print or use online. Perfect for the classroom or homeschooling environment.
Parts of a Number Line
A number line consists of a ray on which the numbers are plotted in an increasing order from left to right. A number line can be divided into three parts –
- Negative Numbers – The negative numbers are plotted to the left of the point 0 or the origin.
- Origin – The number zero ( 0 ) is considered as the origin of the number line and is usually plotted at its centre.
- Positive Numbers – The positive numbers are plotted to the right of the point 0 or the origin.
How to read a Number Line?
Consider the number line below –
Above is a visual representation of a standard number line. As is clearly visible, as we move from left to right, there is an increase in the value of numbers while it decreases when we move from right to left.
Why does a Number Line Do?
What is the purpose of a number in understanding numbers in mathematics?
- A number line helps you visualize which a greater number among two or more numbers is. The farther a number is on the right, the greater it is.
- A number can line can be useful for understanding the comparison as well as the ordering of numbers.
- A number line demonstrates the addition, subtraction, multiplication as well as division of numbers, be it integers, fractions or decimals.
How are Number Lines Useful?
Number Lines are not just an initial representation of numbers on a line. They serve a purpose for the very basic understanding of the concept of numbers and how they move upwards or downwards in the counting tables. Here are some areas where number lines have been found to be extremely useful –
Representation on a Number Line

Above is a visual representation of a standard number line. As is clearly visible, as we move from left to right, there is an increase in the value of numbers while it decreases when we move from right to left.
Examples
1. On which number is the ball sitting on?
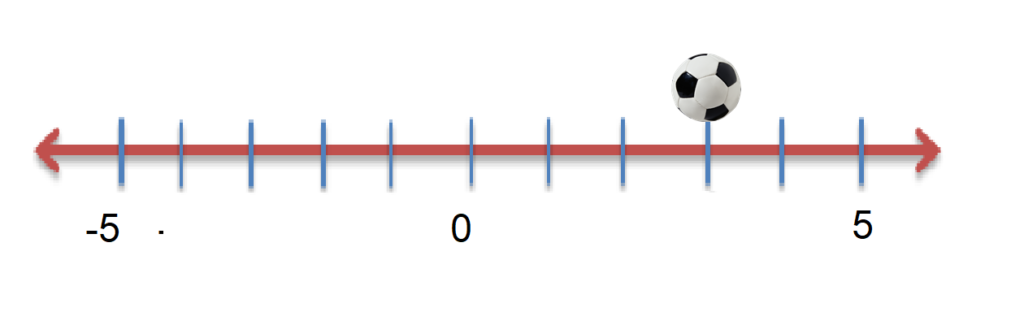
Answer: Count the points from 0 and you will notice that the ball is sitting on number 3.
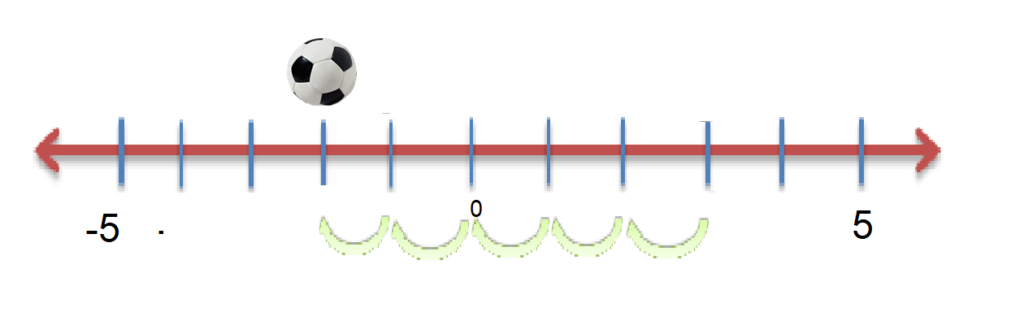
2. Suppose the ball in the example above moves 5 points towards its left side. Which number it would be sitting on now?
Answer: Make the ball jump 5 points towards its left and you would find that it lands on the number -2.
Can Number Lines be placed only in a horizontal manner?
When we think of a number line, we almost always think of numbers placed on a horizontal line. But, is it possible to place the numbers in a vertical manner? Yes, it certainly is possible. It is not that you always need to plot numbers on a number line in a horizontal manner. They can be placed vertically as well. For instance, here is one of the vertical number lines that we have for you –

Not just this, you get the choice of choosing the intervals between the numbers as well while creating a vertical number line.
Finding out the greater number among two or more numbers
A number line helps you visualize which is a greater number among two or more numbers. The farther a number is on the right, the greater it is.
For example, let us consider the following numbers: -2, 8 and 3
Plot these numbers on a number line.
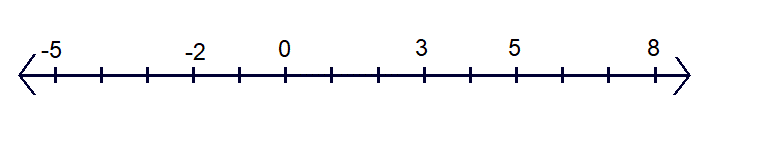
Out of the three given numbers, -2 is on the farthest left while 8 is on the farthest right placing 3 between these numbers.
Hence the increasing orders of the numbers -2, 8 and 3 is
-2 < 3 < 8
Operations on a Number Line
The four basic operations- addition, subtraction, multiplication, and division are the fundamentals of mathematics. The number line is one of the methods that allow visually understanding of these operations.
Addition on a Number Line
We move to the right on our number line for adding two numbers. The following example shall help you understand how to add two numbers to a number line.
For example, you want to add 3 + 2
Steps involved:
1. First draw a number line having both negative as well as positive numbers.

2. Mark the first number 3 on this number line.
3. Move 2 points right as we have to add the numbers.
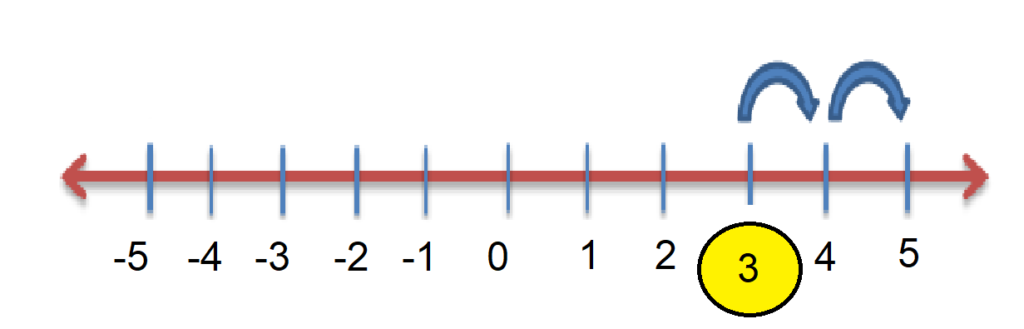
4. The number we have our point on is our answer, i.e. 5
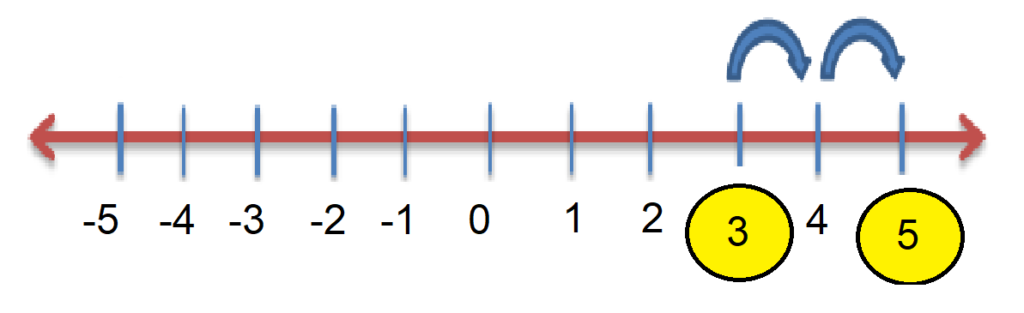
Hence 3 + 2 = 5
Subtraction on a Number Line
Subtraction on a number line is similar to what we do in addition with the only difference being that instead of moving right on the number line, we move left. This can be better understood through the visual depiction of subtraction in the example below –
Suppose we want to obtain the value of 3 – 2
We proceed in the same manner we did for addition.
Steps Involved :
1. First draw a number line having both negative as well as positive numbers.

2. Mark the first number 3 on this number line.

3. Move 2 points left as we have to add the numbers. (Notice the change- we move left and not right as we did in addition)
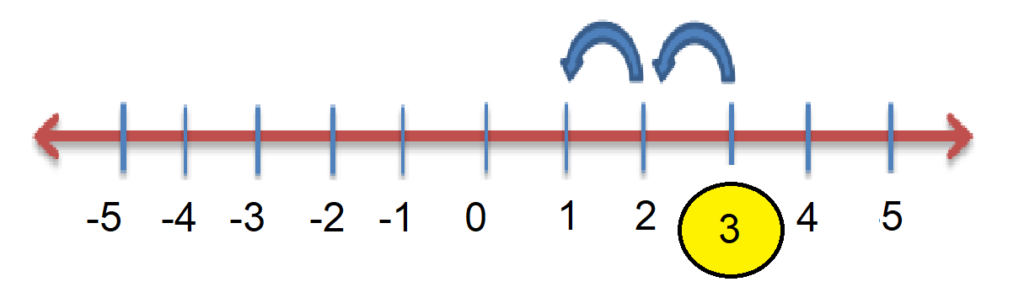
4. The number we have our point on is our answer, i.e. 1
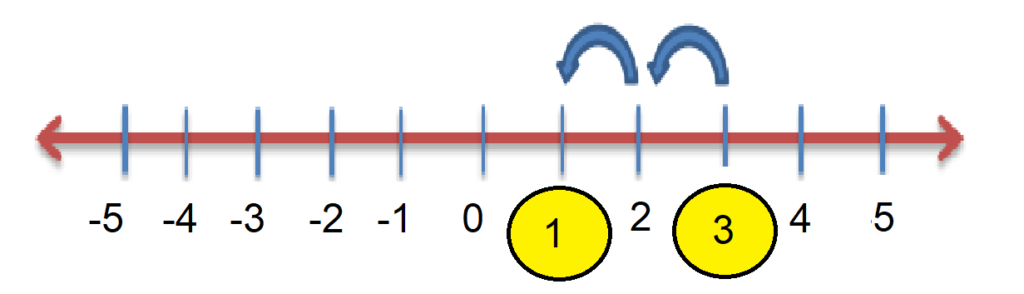
Hence 3 – 2 = 1
Multiplication on a Number Line
Multiplication is nothing but repeated addition. We move towards the right side of the number line for a given number of times in order to multiply two numbers.
For example, we want to obtain the value of 2 x 3
Steps Involved:
- In order to multiply 2 by 3, we first mark 2 on the number line.
- Then we jump 2 points each from 2 three times. The number we land on is our answer, i.e. 6
Hence 2 x 3 = 6
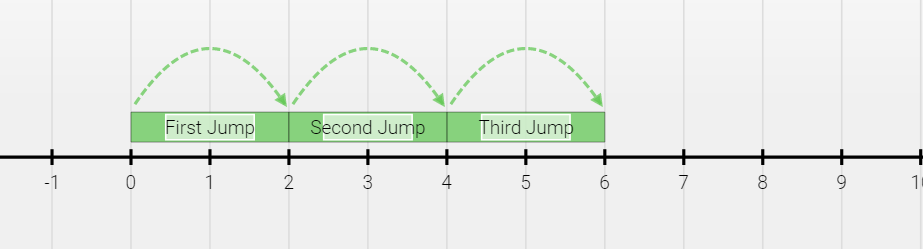
Division on a Number Line
Division on a number line is similar to what we do in multiplication with the only difference being that instead of moving right on the number line, we move left. This can be better understood through the visual depiction of subtraction in the example below.
For example, we want to obtain the value of 12 ÷ 3
Steps Involved:
- First we mark the number 12 on the number line.
- Then we divide the numbers from 0 to 12 into 3 equal groups which gives us the answer 4. Hence 12 ÷ 3 = 4
The above example can be visualized on a number as highlighted below:

Importance of Number Lines
Numbers lines are mostly overlooked and taught as introductory topics for mathematical operations only. However, they form the basics of understanding these very operations that are the backbone of mathematics. Number lines are an important concept as
- They help you visualize the mathematical operations, especially when dealing with negative numbers that make you understand the operations in a better manner.
- Also, they promote good mental arithmetic strategies.
Have you ever noticed the readings of a clinical thermometer? It is based on the concept of number lines. The temperature increases as you move right and decreases as you move left. There are many other examples where number lines are used in real-life situations such as a ruler that we use in everyday life. Find out more about such objects in your house/school and other areas and you will be surprised at the large-scale usage of these number lines.