Alternate Interior Angles

What are Parallel Lines?

Before we understand what we mean by alternate interior angles, we must first recall the basic concepts and terms that are integral to the understanding of alternate interior angles. 

There can be many lines in a plane, some of which may intersect each other while some may not intersect when produced in either direction. Thus we can define parallel lines as – “Two lines l and m in the same plane are said to be parallel lines of they do not intersect when produced indefinitely in either direction.”

Symbolically, two parallel lines l and m are written as l || m.

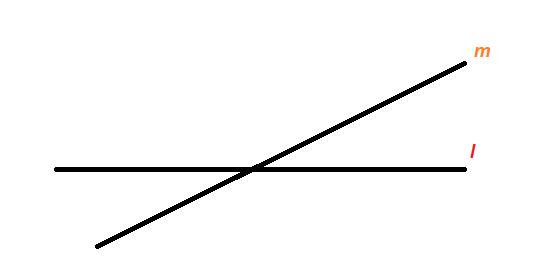
It should be noted that if two lines are not parallel, they will intersect each other. For instance, below we have the lines l and m as intersecting lines as they are not parallel.

Now, what if we have three lines two of which may be parallel to each other while the third one intersects them? This is where we introduce the concept of a transversal.

What is a Transversal?

A transversal is defined as a line intersecting two or more given lines in a plane at different points.  For example, in the figure below, the lines l and m are parallel while the line p is intersecting both the line l and the line m. Hence, the line p is a transversal to the lines l and m.

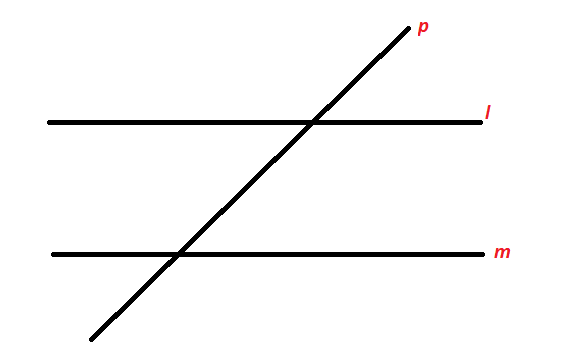
Now, as we can see in the above figure, a transversal makes some angles with the lines it intersects. 

Angles Made by a Transversal with Two Lines

Now, we shall learn about the angles made by a transversal with two given lines. Some of these angles can be paired together by virtue of the positions they occupy.

Let l and m be two lines and let n be the transversal intersecting them at P and Q respectively as shown below – 

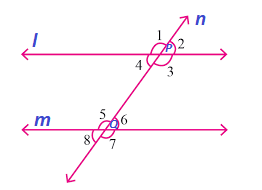
Clearly, lines l and m make eight angles with the transversal n, four at P and four at Q. we have labelled them 1 to 8 for the sake of convenience and shall now classify them in the following groups – 

Exterior Angles of a Transversal

The angles whose arms do not include the line segment PQ are called exterior angles. Therefore, in the above figure, angles 1, 2, 7 and 8 are exterior angles.

Interior Angles of a Transversal

The angles whose arms include the line segment PQ are called interior angles. Therefore, in the above figure, angles 6, 4, 5 and 6 are interior angles.

Corresponding Angles in a Transversal

A pair of angles in which one arm of both the angles is on the same side of the transversal and their other arms are directed in the same sense is called a pair of corresponding angles. In the above figure, there are four pairs of corresponding angles, ∠1 and ∠ 5, ∠ 2 and ∠ 6, ∠ 3 and ∠ 7, ∠ 4 and ∠ 8.

We can also say that two angles on the same side of the transversal are known as corresponding angles if both lie either above the lines or below the two lines.

Alternate Interior Angles in a Transversal

A pair of angles in which one arm of each of the angles is on opposite sides of the transversal and whose other arms include segment PQ is called a pair of alternate interior angles. In other words, Alternate interior angles are angles formed when two parallel or non-parallel lines are intersected by a transversal. The angles are positioned at the inner corners of the intersections and lie on opposite sides of the transversal.

In the above figures, ∠ 3 and ∠ 5 form a pair of alternate interior angles. Another pair of alternate interior angles in this figure is ∠ 4 and ∠ 6.

Alternate Exterior Angles in a Transversal

A pair of angles in which one arm of each of the angles is on opposite sides of the transversal and whose other arms are directed in opposite directions and do not include segment PQ is called alternate exterior angles in a transversal.

In the above figure, ∠ 2 and ∠ 8 form a pair of alternate exterior angles. Another pair of alternate exterior angles in this figure is ∠ 1 and ∠ 7.

Now, we shall learn about the alternate interior angle theorem that is also one of the basic properties of alternate interior angles.

Alternate Interior Angles Theorem

The alternate interior angles theorem states that “The alternate interior angles are congruent when the transversal intersects two parallel lines.”  The converse of the alternate interior angle theorem also holds true. The Converse of the Alternate Interior Angle Theorem states that “If two lines are cut by a transversal and the alternate interior angles are congruent, then the lines are parallel.”

Properties of Alternate Interior angles

The following are the properties of alternate interior angles – 

1. If two parallel lines are cut by a transversal, then the pairs of alternate interior angles are congruent. 
2. Consecutive interior angles are supplementary. Here, it is important to note that consecutive interior angles are interior angles that are on the same side of the transversal line.
3. Alternate interior angles don’t have any specific properties in the case of non – parallel lines.

How to Identify Alternate Interior Angles?

We have learnt that when a transversal intersects a pair of lines, alternate interior angles are formed on opposite sides of the transversal. Also, if the pair of lines are parallel then the alternate interior angles are equal to each other. So, how do we identify the alternate interior angles even if the angles have not been numbered?

 One way of finding the alternate interior angles is by using the z-pattern. We can notice in the figure below that the alternate interior angles form a Z pattern.

Now that we have learnt how to identify alternate interior angles, we shall now learn how to use alternate interior angles to find missing angles. 

How to use the Alternate Angle Theorem to find missing angles?

We have seen that eight angles are formed when two lines are intersected by a transversal. So, how can use alternate interior angles to find the remaining angles? We shall understand this by an example.  

Suppose we have the figure below where ∠ 4 = 60^o.  We shall use this value to find the remaining seven angles formed by the intersection of the two lines by a transversal.

Let us start with each angle one by one.

First, let us find ∠ 3. We can clearly see that ∠ 4 and ∠ 3 form a supplementary pair of angles. This means that the sum of ∠ 4 and ∠ 3 should be equal to 180^o. Hence, we have,

 ∠ 4 + ∠ 3 = 180^o

⇒ 60^o + ∠ 3 = 180^o

⇒ ∠ 3 = 180^o – 60^o 

⇒ ∠ 3 = 120^o

Now, that we have found the value of ∠ 3, we will find the value of ∠ 6

Note that ∠ 4 and ∠ 6 form a pair of alternate interior angles. Since the lines that have been intersected by a transversal are parallel, therefore, the pair of alternate interior angles should be equal. Hence, we have,

∠ 4 = ∠ 6 =  60^o

Similarly, ∠ 3 = ∠ 5 =  120^o

Now, we can see that ∠ 6 and ∠ 7 form a supplementary pair of angles. This means that the sum of ∠ 6 and ∠ 7 should be equal to 180^o. Hence, we have,

∠ 6 + ∠ 7 = 180^o

⇒ 60^o + ∠ 7 = 180^o

⇒ ∠ 7 = 180^o – 60^o 

⇒ ∠ 7 = 120^o

Similarly, we can see that ∠ 5 and ∠ 8 form a supplementary pair of angles. This means that the sum of ∠ 5 and ∠ 8 should be equal to 180^o. Hence, we have,

∠ 5 + ∠ 8 = 180^o

⇒ 120^o + ∠ 8 = 180^o

⇒ ∠ 8 = 180^o – 120^o 

⇒ ∠ 8 = 60^o

Again, we can see that ∠ 2 and ∠ 3 form a supplementary pair of angles. This means that the sum of ∠ 2 and ∠ 3 should be equal to 180^o. Hence, we have,

∠ 2 + ∠ 3 = 180^o

⇒ 120^o + ∠ 2 = 180^o

⇒ ∠ 2 = 180^o – 120^o 

⇒ ∠ 2 = 60^o

Last, we can see that ∠ 1 and ∠ 4 form a supplementary pair of angles. This means that the sum of ∠ 1 and ∠ 4 should be equal to 180^o. Hence, we have,

∠ 1 + ∠ 4 = 180^o

⇒ 60^o + ∠ 1 = 180^o

⇒ ∠ 1 = 180^o – 60^o  ⇒ ∠ 1 = 120^o

Applications of Alternate Interior angles

Here are some of the applications of alternate interior angles – 

1. The most famous application of alternate interior angles one from the famous Greek scientific writer, Eratosthenes, who made use of alternate interior angles to prove that the Earth is round.
2. The windows, with panes divided by mun-tins, have alternate interior angles.
3. In a letter Z, the top and bottom horizontal lines are parallel and the diagonal line is transversal. So, there are two alternate interior angles in a letter Z.

Solved Examples

Example 1 We have two angles ( 4 x – 19 )^o and ( 3 x + 16 )^o which are congruent alternate interior angles. Find the value of x and also determine the value of the other pair of alternate interior angles.

Solution We have been given the alternate interior pair of angles as ( 4 x – 19 )^o and ( 3 x + 16 )^o. it has also been mentioned that this pair of alternate interior angles is congruent. This means that the two angles will be equal. Therefore, we have,

( 4 x – 19 )^o  =  ( 3 x + 16 )^o

⇒ 4 x – 19 = 3 x + 16

⇒ 4 x – 3 x  = 16 + 19

⇒ x = 35

Hence, x = 35 and the two alternate interior angles are 

4 x – 19 = 4 x ( 35 )  – 19 = 140 – 19 = 121^o

and

3 x + 16 = 3 x ( 35 ) + 16  = 105 + 16 = 121^o

Since we have obtained the same value of the two angles, this further proves our result to be true as the angles have been said to be congruent, hence equal.

Now, we know that angles formed on the same side of the transversal are supplementary angles. Then, the value of the other pair of alternate interior angles will be – 

180 ^o – 121 ^o = 59 ^o

Example 2 If (2 x + 26) ° and (3 x – 33) ° are alternate interior angles that are congruent, find the measurement of the two angles.

Solution We have been given that (2 x + 26) ° and (3 x – 33) ° are alternate interior angles that are congruent. Now we know that if alternate interior angles are congruent, this means that the angles will be equal.

Hence,

(2 x + 26) ° = (3 x – 33) °

⇒ 2 x  + 26 = 3 x  – 33

⇒ 2 x – 3 x = – 33 – 26

⇒ –  x  = 59

⇒   x  = 59

Now, we have,

2 x  + 26 = 2 ( 59 ) + 26 = 11 8 + 26 = 144^o

Also, 3 x  – 33 = 3 ( 59 ) – 33 = 177 – 33 = 144^o

Hence, the measurement of the angles is 144^o

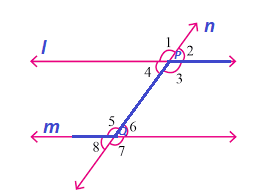
Example 3 In the given figure, the lines l and m are parallel. n is a transversal and ∠ 1 = 40^o. Find all the angles marked in the figure.

Solution We have been given that lines l and m are parallel. n is a transversal and ∠ 1 = 40^o. we need to find the remaining angles.

Let us start with each angle one by one.

First, let us find ∠ 2. We can clearly see that ∠ 1 and ∠ 2 form a supplementary pair of angles. This means that the sum of ∠ 1 and ∠ 2 should be equal to 180^o. Hence, we have,

 ∠ 1 + ∠ 2 = 180^o

⇒ 40^o + ∠ 2 = 180^o

⇒ ∠ 2 = 180^o – 40^o 

⇒ ∠ 2 = 140^o

Now, that we have found the value of ∠ 2, we will find the value of ∠ 6

Note that ∠ 2 and ∠ 6 form a pair of corresponding angles. Since the lines that have been intersected by a transversal are parallel, therefore, the pair of corresponding angles should be equal. Hence, we have,

∠ 2 = ∠ 6 =  140^o

Similarly, ∠ 1 = ∠ 5 =  40^o

Note that ∠ 3 and ∠ 5 form a pair of alternate interior angles. Since the lines that have been intersected by a transversal are parallel, therefore, the pair of alternate interior angles should be equal. Hence, we have,

∠ 3 = ∠ 5 =  40^o

Similarly, ∠ 4 = ∠ 6 =  140^o

Similarly, we can see that ∠ 5 and ∠ 8 form a supplementary pair of angles. This means that the sum of ∠ 5 and ∠ 8 should be equal to 180^o. Hence, we have,

∠ 5 + ∠ 8 = 180^o

⇒ 40^o + ∠ 8 = 180^o

⇒ ∠ 8 = 180^o – 40^o 

⇒ ∠ 8  =  140^o

Again, we can see that ∠ 6 and ∠ 7 form a supplementary pair of angles. This means that the sum of ∠ 6 and ∠ 7 should be equal to 180^o. Hence, we have,

∠ 6 + ∠ 7 = 180^o

⇒ 140^o + ∠ 7 = 180^o

⇒ ∠ 7 = 180^o – 140^o 

⇒ ∠ 7 = 40^o

Hence, we have, ∠ 1 = ∠ 3 = ∠ 5 = ∠ 7 = 40^o and ∠ 2 = ∠ 4 = ∠ 6 = ∠ 8 = 140^o

Key Facts and Summary

1. Two lines l and m in the same plane are said to be parallel lines of they do not intersect when produced indefinitely in either direction.
2. If two lines are not parallel, they will intersect each other.
3. A transversal is defined as a line intersecting two or more given lines in a plane at different points.  
4. The angles whose arms include the line segment that forms the transversal are called interior angles.
5. A pair of angles in which one arm of both the angles is on the same side of the transversal and their other arms are directed in the same sense is called a pair of corresponding angles.
6. Alternate interior angles are angles formed when two parallel or non-parallel lines are intersected by a transversal.
7. The alternate interior angles are congruent when the transversal intersects two parallel lines.
8. If two lines are cut by a transversal and the alternate interior angles are congruent, then the lines are parallel.
9. The most famous application of alternate interior angles one from the famous Greek scientific writer, Eratosthenes, who made use of alternate interior angles to prove that the Earth is round.

Recommended Worksheets

Parallel lines Cut by a Transversal 8th Grade Math Worksheets
Angles (Architecture Themed) Worksheets
Angle Measurements (Cruise Ship Themed) Worksheets