Home » Math Theory » Geometry » Different Types Of Shapes

Different Types Of Shapes

What are Shapes?

The boundary or outline of an object is called its shape. We come across many shapes in our daily lives and kids start recognising these shapes even before actually studying about them. The alphabets of English shapes are all shapes of different types. The Sun, the earth and other planets, the mountains and all other things in the world are all of the specific shapes. Let us learn more about these shapes.

Types of Shapes

To start with it is important to understand how do we categorise different shapes? The first basic categorisation is based upon the nature of the line segments they are made of, i.e. whether those line segments form a closed loop or are open-ended. Based on the structure, the shapes are classified into two categories:

  • Open Shapes
  • Closed Shapes

Next, we have the number of line segments that are required to form a shape. For instance, we may need three line segments for a particular shape while another shape may need line segments. Therefore, based on the number of line segments, the shapes can be classified as – triangles, quadrilaterals, pentagon, hexagon etc.

Further, the shapes can be classified based upon the dimensions they have. A shape may be:

  • 2 Dimensional
  • 3 Dimensional

Let us study these shapes in further detail.

Open and Closed Shapes

As we have learnt, the first basic categorisation is based upon the nature of the line segments they are made of, i.e. whether those line segments form a closed loop or are open ended.

Open Shapes – The shapes that are made of line segments that do not meet are called open shapes. This means that these shapes have open ends and are not closed, for example, the letter C is an open shape as its ends do not meet.

Closed Shapes – The shapes that are made of line segments that formed closed loops are called closed shapes. They start and end at the same point. For example, a ball is a closed shape. A simple closed figure formed of three or more line segments is called a polygon.

2D and 3D Shapes

The shapes can be classified based upon the dimensions they have. The three dimensions are length, breadth and height.

2D shapes – 2 Dimensional shapes or 2D shapes are the shapes that have only length and breadth. For example, the shapes such as rectangles and squares are 2-dimensional shapes.

3D shapes – 3 Dimensional shapes or 3D shapes are the shapes that have all the three dimensions, i.e. length, breadth and height.                                          

Vertex and Sides

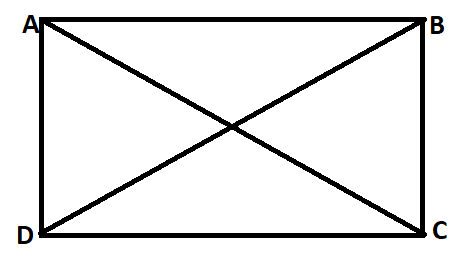
Vertex – The meeting point of a pair of sides of a polygon is called its vertex. For example, the shapes such as cube and cuboid are 3-dimensional shapes. For example, in the below figure, ABCD, the vertices are A, B, C and D.

Side – The line joining two vertices is called a side. For example, in the above polygon, ABCD, AB is one of the sides of the polygon.

Adjacent Sides – Any two sides of a polygon having a common end point are called its adjacent sides. For example, in the given polygon ABCD, the four adjacent pairs of sides are ( AB, BC ), ( BC, CD ), ( CD, DA ) and ( DA, AB ).

Angles – The three angles are the angles made at these vertices, i.e. ∠A, ∠B and ∠C.  The angle formed at A can also be written as ∠BAC. Similarly, we can write ∠ABC and ∠ACB. These angles are also called the interior angles of a triangle. An exterior angle of a triangle is formed by any side of a triangle and the extension of its adjacent side.

Diagonals – A line segment joining the two non-adjacent vertices of a polygon is called its diagonal. For example, in the given polygon ABCD, A and C are non-adjacent vertices. Similarly, B and D are non-adjacent vertices.  Therefore lines BD and AC are the diagonals of the polygon ABCD.

Let us now study some commonly sued shapes in mathematics as well as everyday life.

2D Shapes

As we have studies that the shapes that have only length and breadth are called 2D shapes. These shapes are further classified based on the number of line segments they are made of. Some of the common shapes are triangles, quadrilaterals, pentagons and other polygons. Let us understand these in detail.

Triangle

A triangle is a polygon that is made up of 3 sides, 3 angles and three vertices. For example, let us have a triangle ABC as shown in the figure below.

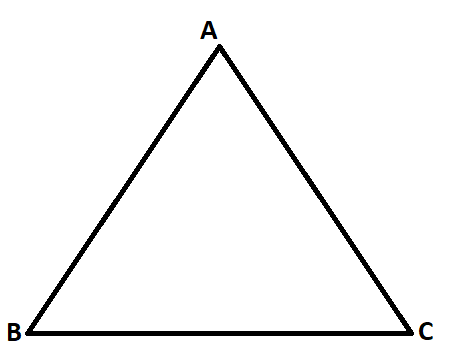
In this triangle,

  • the three vertices are – A, B and C
  • the three sides are AB, BC and AC
  • the three angles are ∠A, ∠B and ∠C

Properties of a triangle

The properties of a triangle are :

  • Sides, Angles and Vertices – We already know that a triangle always has exactly three sides and three vertices. This is the basic property of any triangle.
  • Angle Sum Property of a Triangle – The sum of the measure of the three interior angles of a triangle is always 180o.
  • Pythagoras Theorem – If one of the angles of a triangle is 90o, the sides that make the right angle is called the base and the perpendicular while the third side is called the hypotenuse.

Quadrilaterals

A quadrilateral is a closed shape that is formed by joining four points among which any three points are non-collinear. In other words, a quadrilateral is a polygon made up of four sides. The order of vertices needs to be kept in mind while naming a quadrilateral.

For instance, below we have a quadrilateral ABCD

This quadrilateral cannot be named as ABDC as the vertices B and D are not adjacent.

Also, all the quadrilaterals have the same number of sides and angles, there may be a difference in the measurement of these sides and angles due to which we have different types of quadrilaterals. But, there are some properties of quadrilaterals that apply to all irrespective of their unique properties. These properties are:

  1. All the quadrilaterals have four sides.
  2. All the quadrilaterals have four angles
  3. All the quadrilaterals have four vertices
  4. The sum of the four angles of the quadrilateral is 360o
  5. All the quadrilaterals have two diagonals

Let us now learn about different types of quadrilaterals.  

Rectangle

A rectangle is a type of quadrilateral that has equal opposite sides and four right angles. The properties of a rectangle are:

  1. A rectangle has two pairs of parallel sides
  2. A rectangle has four right angles
  3. A rectangle has opposite sides of equal lengths
  4. The diagonals of a rectangle bisect each other

Let us understand each of the above properties through the below rectangle ABCD.

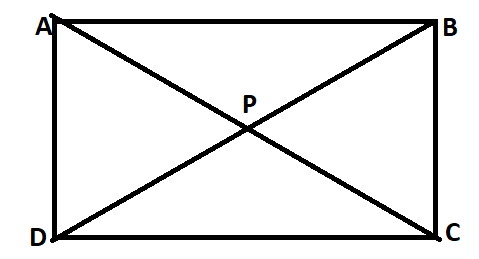
  1. The rectangle ABCD has two pairs of parallel sides, namely (AB and CD) and (AD and BC)
  2. The rectangle ABCD has four right angles, namely at ∠A, ∠B, ∠C and ∠D.
  3. The rectangle ABCD has opposite sides of equal lengths, i.e. AB = CD and AD = BC
  4. The diagonals of the rectangle bisect each other, i,e. AP = PC and BP = PD 

Square

A square is a quadrilateral that has four equal sides and four right angles.

The properties of a square are:

  1. A square has four equal sides, i.e. all the sides of a square are equal.
  2. A square has four right angles
  3. A square has two pairs of parallel sides
  4. The diagonals of a square bisect each other
  5. The diagonals of a square are perpendicular to each other

Let us understand each of the above properties through the below square ABCD.

  1. The square ABCD has two pairs of parallel sides, namely (AB and CD) and (AD and BC)
  2. The square ABCD has four right angles, namely at ∠A, ∠B, ∠C and ∠D.
  3. The square ABCD has all sides equal, i.e. AB = CD = AD = BC
  4. The diagonals of the square ABCD bisect each other, i,e. AP = PC and BP = PD
  5. The diagonals of the square ABCD are perpendicular to each other, i,e. AC ⟂ BD.

Parallelogram

A parallelogram is a quadrilateral in which both pairs of opposite sides are parallel.

The properties of a parallelogram are:

  1. A parallelogram has opposite sides of equal lengths. 
  2. The opposite angles of a parallelogram are equal.
  3. A parallelogram has two pairs of parallel sides
  4. The diagonals of a parallelogram bisect each other

Let us understand each of the above properties through the below parallelogram ABCD.

  1. The parallelogram ABCD has two pairs of parallel sides, namely (AB and CD) and (AD and BC)
  2. The parallelogram ABCD has opposite angles equal, i.e. ∠A = ∠C and ∠B  = ∠D.
  3. The parallelogram ABCD has opposite sides of equal lengths, i.e. AB = CD and AD = BC
  4. The diagonals of the parallelogram bisect each other, i,e. AP = PC and BP = PD 

Trapezium

A trapezium is a quadrilateral in which one pair of opposite sides is parallel.

The properties of a trapezium are:

  1. A trapezium has one pair of parallel sides
  2. A trapezium has no right angles
  3. A trapezium has one pair of opposite sides of equal lengths

Let us understand each of the above properties through the below trapezium ABCD.

  1. The trapezium ABCD has one pair of parallel namely (AB and CD)
  2. No angle in a trapezium is a right angle.
  3. The trapezium ABCD one pair of opposite sides of equal lengths, i.e. AD and BC

Rhombus

A rhombus is a quadrilateral with four equal sides.

The properties of a rhombus are:

  1. A rhombus has two pairs of parallel sides
  2. The opposite angles in a rhombus are equal.
  3. A rhombus has four equal sides. This means that all its sides are equal.
  4. The diagonals of a rhombus bisect each other
  5. The diagonals of a rhombus are perpendicular each other

Let us understand each of the above properties through the below rhombus ABCD.

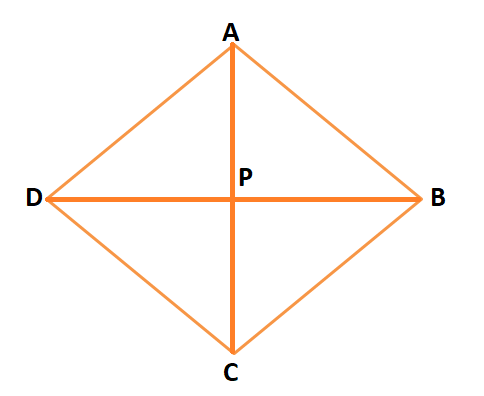
Let us understand each of the above properties through the below rhombus ABCD.

  1. The rhombus ABCD has two pairs of parallel sides, namely (AB and CD) and (AD and BC)
  2. The rhombus ABCD has all sides equal, i.e. AB = CD = AD = BC
  3. The rhombus ABCD has opposite angles equal, i.e. ∠A = ∠C and ∠B  = ∠D.
  4. The diagonals of the rhombus bisect each other, i,e. AP = PC and BP = PD 
  5. The diagonals of the rhombus ABCD are perpendicular to each other, i,e. AC ⟂ BD.

Circles

A circle is a two-dimensional figure formed by a set of points that are at a constant or at a fixed distance from a fixed point in the plane. This fixed distance is called the radius of the circle and the fixed point is called the centre of the circle.

Parts of a Circle

Circumference – The circumference of a circle is the distance around the boundary of the circle. In other words, it is the perimeter of the circle.

Radius – Radius is the distance from the centre of a circle to any point on the boundary of the circle. 

Diameter – Diameter is the line from one point on the boundary of the circle to another point and passing through the centre of the circle. It is twice the length of the radius.

Chord of a Circle – The chord of a circle is the line from one point on the boundary of the circle to another point. The diameter is the longest chord of a circle.

Arc of a Circle – A part of a portion of the circumference of the circle is called its arc.

Let us understand the above parts of a circle through the following figure.

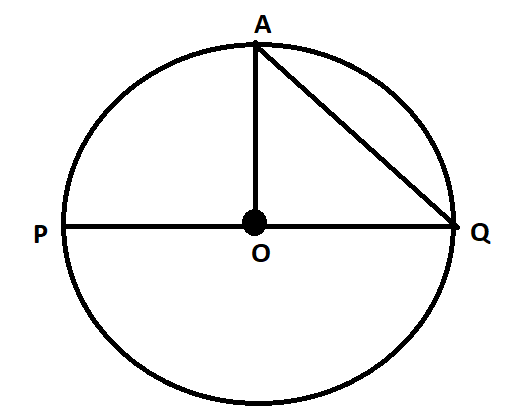
In the circle above,

O is the centre of the circle.

The line segment AO is the radius of the circle.

The lone segment PQ is the diameter of the circle. Note that the line segment PQ is passing through the centre O

The line segment AQ is a chord of the circle that joins two points A and Q that lie on the boundary of the circle.

The curve formed by AQ is the arc of the circle.

3D Shapes

3 Dimensional shapes or 3D shapes are the shapes that have all the three dimensions, i.e. length, breadth and height. The room of a house is a common example of a 3 d shape. Let us understand some of these shapes in detail. Some common terms used to define the 3D shapes are:

  • Faces – A face refers to any single flat surface of a 3D shape.
  • Edges – An edge is a line segment on the boundary joining one vertex (corner point) to another. It is similar to the sides we have in 2D shapes.
  • Vertices – The meeting point of a pair of sides of a polygon is called its vertex.

Let us now understand some of the common 3D shapes.

Cuboid

A 3D shape having six rectangular faces is called a cuboid. Ex a matchbox, a brick, a book etc. In other words, it is an extension of a rectangle in a 3D plane.

Below we have a general diagram of a cuboid

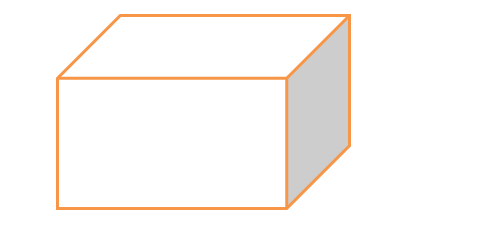
Faces: A cuboid has 6 rectangular faces, out of which the opposite sides are identical.

Edges: A cuboid has 12 eddges

Vertx: A cuboid has 8 vertices

Cube

A cuboid whose length, breadth and height are equal is called a cube. Examples of a cube are sugar cubes, cheese cubes and ice cubes. In other words, it is an extension of a square in a 3D plane.

Below we have a general diagram of a cube

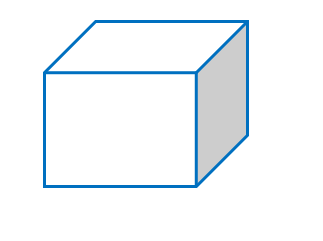
Faces: A cube has 6 rectangular faces, out of which all are identical.

Edges: A cube has 12 edges

Vertx: A cube has 8 vertices

Cylinder

A cylinder is a solid with two congruent circles joined by a curved surface.

Below we have a general diagram of a Cylinder

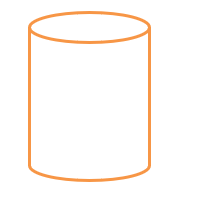
Faces: A cylinder has one curved surface and two flat faces.

Edges: A cylinder has two curved edges.

Vertx: A cylinder has no vertices.

Cone

A circular cone has a circular base that is connected by a curved surface to its vertex. A cone is called a right circular cone if the line from its vertex to the centre of the base is perpendicular to the base. An ice-cream cone is an example of a cone

Below we have a general diagram of a Cone

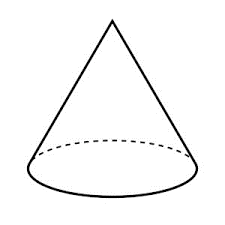
Faces: A cone has one flat face and one curved surface.  

Edges: A cone has one curved edge.

Vertx: A cone has one vertex. 

Sphere

A sphere is a solid formed by all those points in space that are at the same distance from a fixed point called the centre.  In other words, it is an extension of a circle in a 3D plane.

Below we have a general diagram of a Sphere

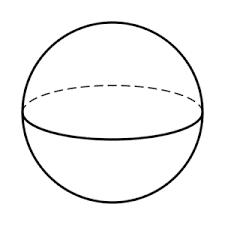
Faces: A cone has one curved surface. 

Edges: A cone has no edge.

Vertx: A cone has no vertex. 

2-D and 3-D Shapes Kindergarten Math Worksheets
Area of a Circle (Home Decorations & Furniture Themed) Worksheets
Shape Transformations (International Literacy Day Themed) Math Worksheets

Browse All Worksheets

Link/Reference Us

We spend a lot of time researching and compiling the information on this site. If you find this useful in your research, please use the tool below to properly link to or reference Helping with Math as the source. We appreciate your support!

  • "Different Types Of Shapes". Helping with Math. Accessed on April 20, 2024. https://helpingwithmath.com/different-types-of-shapes/.

  • "Different Types Of Shapes". Helping with Math, https://helpingwithmath.com/different-types-of-shapes/. Accessed 20 April, 2024.

  • Different Types Of Shapes. Helping with Math. Retrieved from https://helpingwithmath.com/different-types-of-shapes/.