Area of a Circle

What is Area?

The amount of space covered by a flat surface or piece of land or an object is called its area. The coloured part of each of the following figures shows the amount of space covered by each of them on a sheet of paper. 

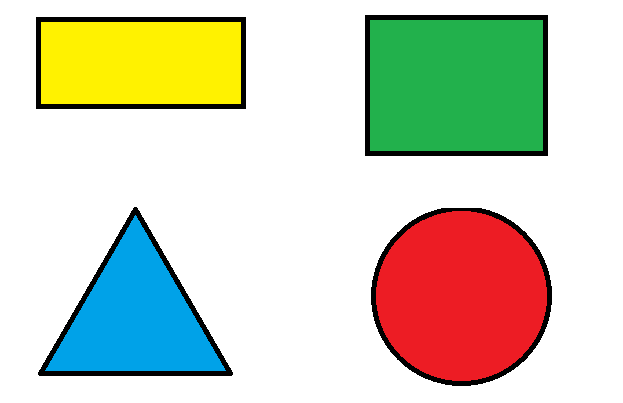
Units of measurement of Area

The units used to measure area are based on the units of length, i.e. mm, cm, m, km etc. to measure a region we use a square as a unit. Hence, the unit of area is a unit square. This is written as unit². Let us see who the different units are used to represent the area of a surface.

Unit – Area

mm – mm² (1 mm² is equal to 1 square millimetres)

cm – cm² (1 cm² is equal to 1 square centimetres)

m – m² (1 m² is equal to 1 square metres)

km – km² (1 km² is equal to 1 square kilometres)

mi – mi² (1 mi² is equal to 1 square miles)

What is a Circle?

Before learning how to find the area of a circle, let us first recall what we mean by a circle?

A circle is the set of all those points in a plane whose distance from the fixed point remains constant. The fixed point is called the centre of the circle and the constant distance is known as the radius of the circle. The line segment passing through the centre of a circle and having its end points on the circle is called the diameter of the circle. 

Parts of a Circle

Below are some more terms that are integral to the understanding of the area of a circle – 

Circular Region – The part of the circle that consists of the circle and its interior is called the circular region. 

Chord of a Circle – A line segment joining any two points on a circle is called a chord of the circle.

Circumference of a Circle – The perimeter of a circle is called the circumference of the circle. The ratio of the circumference of a circle and its diameter is always constant.

Concentric Circles – Circles having the same centre but with different radii are said to be concentric circles. Following is an example of concentric circles – 

Arc of a Circle: An arc of a circle is referred to as a curve that is a part or portion of its circumference. Acute central angles will always produce minor arcs and small sectors. When the central angle formed by the two radii is 90^o, the sector is called a quadrant because the total circle comprises four quadrants or fourths. When the two radii form a 180^o, or half the circle, the sector is called a semicircle and has a major arc.

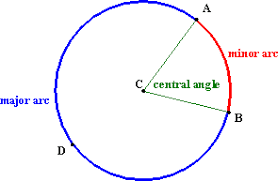
Segment in a Circle: The area enclosed by the chord and the corresponding arc in a circle is called a segment. There are two types of segments – minor segment, and major segment.

Sector of a Circle: The sector of a circle is defined as the area enclosed by two radii and the corresponding arc in a circle. There are two types of sectors, minor sector, and major sector.

The Number π 

We know that the circumference of a circle is in constant ratio to its diameter. This constant is denoted by the Greek letter π which is read as “pie”. This constant π is not a rational number. Therefore, it cannot be written as a terminating or a non-terminating decimal. The value of π correct to 2 places of decimal is 3.14 and in fractions it is  $\frac{22}{7}$ . 

What is Area of a Circle?

The space occupied by a circle is called its area. 

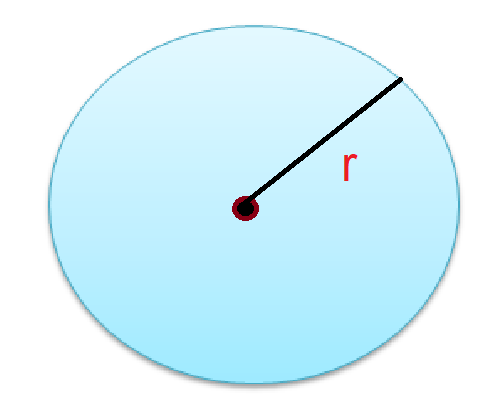
The area of a circle having a radius ‘r’ (The distance from the centre to a point on the boundary) is given by πr² where π = $\frac{22}{7}$ or 3.14 (approx.)

For example, suppose we have a circle that has a radius of 7 cm as shown in the figure below.

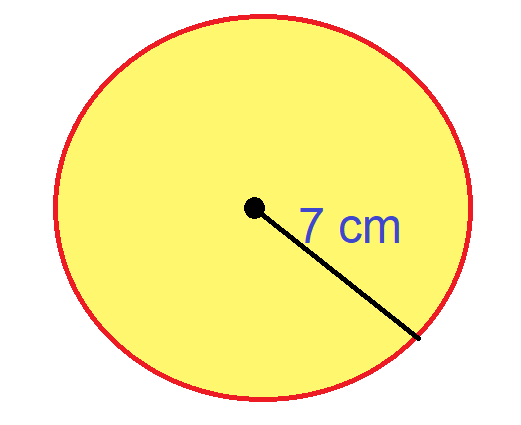
 Its area is given by – 

Area = πr² = $\frac{22}{7}$ x 7 x 7 = 154 cm²

Suppose, instead of the radius we are given the diameter of a circle, how do we calculate the area?

We know that in a circle, the radius is half of the diameter. Mathematically,

r = $\frac{d}{2}$, where ‘d’ is the diameter and ‘r’ is the radius.

So, we half the given diameter and obtain the radius.

Now, what is we want to find the area of a Semicircle?

Area of a Semi-Circle = $\frac{1}{2}$ ( Area of the circle ) = $\frac{1}{2}$ πr²

Let us understand the area of a circle through some examples.

Example 1

Suppose we are required to find the area of a circle having a diameter of 4.2 cm.

Here diameter (d) = 4.2 cm

By the relation between radius and diameter, we have, r = $\frac{d}{2}$

Hence r = $\frac{4.2}{2}$ = 2.1 cm

Now, area of this circle = = πr² = $\frac{22}{7}$ x 4.2 x 4.2 = 55.44 cm²

Example 2

Four equal circles are described about four corners of a square so that each touches two of the others, as shown in the figure. Find the area of the shaded region, if each side of the square measures 14 cm.

Solution

Let ABCD be the given square each of which is 14 cm long. Clearly, the radius of each circle is 7 cm.

We have,

Area of the square of side 14 cm long = (14 x 14) cm² = 196 cm²

Area of the quadrant of a circle of radius 7 cm

 = $\frac{1}{4}πr^2$

 = $\frac{1}{4} x \frac{22}{7}$ x 7² cm²

 = 38.5 cm²

Therefore, area of four quadrants = 4 x 38.5 cm² = 154 cm²

Hence,

Area of the shaded region 

= Area of the square ABCD  – Area of 4 quadrilaterals

= (196 – 154) cm²

= 42 cm²

Area of a Sector of a Circle

We have learnt that a sector is a portion of a circle enclosed between its two radii and the arc adjoining them. Hence, the area of a sector is the region enclosed by the two radii of a circle and the arc. In simple words, the area of a sector is a fraction of the area of the circle. We need to know the following parameters in order to find the area of a sector of a circle – 

1. The length of the circle’s radius.
2. The measure of the central angle or the length of the arc. It is important to understand here that the central angle is the angle subtended by an arc of a sector at the centre of a circle. The central angle can be given in degrees or radians.

There are three ways in which we can find the area of a sector of a circle – 

1. Area of a sector when the central angle is given in degrees
2. Area of a sector given the central angle in radians
3. Area of a sector given the arc length

Let us know about them one by one.

Area of a sector when the central angle is given in degrees

The following formula is used if the angle of the sector is given in degrees – 

Area of a Sector  = ( $\frac{\theta}{360}$) π r²

where $\theta$ = central angle in degrees, and

r = radius of the sector. 

Area of a sector given the central angle in radians

Recall that radians are based on π (a circle is 2π radians). The following formula is used if the angle of the sector is given in radians – 

Area of a Sector  = $\frac{(\theta r^2)}{2}$

where θ = the measure of the central angle given in radians and r = radius of the sector

Area of a sector given the arc length

The following formula is used if the length of the arc is given – 

Area of a Sector  = r $\frac{L}{2}$

where,  L = length of the arc and r = radius of the sector.

Area of a Circle in a 3D Plane

If we look at a circle in a 3D plane, it will take the shape of a sphere. The sphere can thus be defined as – “A sphere is a solid formed by all those points in space that are at the same distance from a fixed point called the centre”. Therefore, to find the area we will have to calculate the area of the circular shape obtained in the form of a sphere. This area is known as the Surface area of the Sphere. Below is a representation of a sphere.

Surface Area of the Sphere

Surface Area of a sphere of radius r is given by S = 4πr² units.

Let us understand the above formula through an example.

Example

Find the surface area of a sphere of radius 7 cm

Solution

We have learnt that the surface area S of a sphere of radius r is given by S = 4πr² units.

Here, we have r = 7 cm.

Therefore, surface area of the sphere = 4πr² = 4π7²

S = 4 x $\frac{22}{7}$ x 7 x 7 = 616 cm²

Hence, the surface area of the given sphere = 616 cm²

Solved Examples

Example 1 The diameter of a circular plate is 20 cm. Find the dimensions of a square plate that will have the same area as the circular plate.

Solution We have been given that the diameter of a circular plate is 20 cm. we need to find dimensions of a square plate that will have the same area as the circular plate. To find this, we will first equate the area of the circle to the area of the square. This means that

πd²/4 = s²

3.14 x 20²/4 = s²

s² =314

No, we will find the square root of both sides to get,

s = 17.72

Therefore, the dimensions of the square plate will be 17.72 cm by 17.72 cm.

Example 2 Calculate the area of a sector with a radius of 10 metres and an angle of 90 degrees.

Solution We have learnt that 

Area of a Sector  = ( $\frac{\theta}{360}$ ) π r²

Now, we have been given that the radius of the sector is equal to 10 metres while the angle is of 90 degrees. Substituting these values in the above formula, we get – 

Area of a Sector  = ( $\frac{90}{360}$ ) x  3.14 x 10 x 10

= 78.5 sq. metres

Hence, area of the sector = 78.5 sq. metres

Example 3 Find the area of a sector whose arc is 8 inches and radius is 5 inches.

Solution We have learnt that area of a sector if we have been given the arc length = r $\frac{L}{2}$, where,  L = length of the arc and r = radius of the sector.

Now, we have been given that arc is 8 inches and radius is 5 inches. This means that,

Radius = r = 5 inches

Length of the arc = L = 8 inches

Area of a sector = r $\frac{L}{2}$

⇒ Area of a sector = 5 x $\frac{8}{2}$ = 5 x 4 = 20 sq. inches.

Hence, area of the sector = 20 sq. inches.

Example 4 A copper wire when bent in the form of a square encloses an area 484 sq. cm. If the same wire is bent in the form of a circle, find the area enclosed by it. ( Use π = $\frac{22}{7}$ )

Solution We have been given that a copper wire when bent in the form of a square encloses an area 484 sq. cm and the same wire is bent in the form of a circle. 

So,

Area of the square = 484 sq. cm

We know that area of a square = Side x Side

Therefore,

Side x Side = 484 sq. cm

Side² = 22² cm

⇒ Side = 22 cm

Now, we know that the perimeter of the square = 4 x Side

Hence,

Perimeter of the square =  4 x 22 = 88 cm

Now, let r be the radius of the circle. Then,

Circumference of the circle = Perimeter of the square

   ⇒ 2 π r  = 88

⇒ 2 x $\frac{22}{7}$ x r = 88

⇒ r = 14 cm

Now, we know that area of a circle = π r²

Therefore, we have,

π r² = $\frac{22}{7}$ x 14 x 14 = 616 cm²

Hence, the area enclosed by the circle will be 616 cm²

Example 5 The area of two circles are in the ratio 16 : 25. Find the ratio of their circumferences.

Solution We have been given that the area of two circles are in the ratio 16 : 25. Let r₁ and r₂ be the radii of two circles and let their area be A₁ and A₂ respectively. Then,

Therefore, we have,

A₁ = πr₁² and A₂ =  πr₂²

Now, we have been given that A₁ : A₂ = 16 : 25

⇒ πr₁² : πr₂² = 16 :  25

⇒ $\frac{π r_{1}^{2}}{π r_{2}^{2}} = \frac{16}{25}$

⇒ $\frac{r_{1}^{2}}{r_{2}^{2}} = \frac{16}{25}$

⇒ $\frac{r_{1}^{2}}{r_{2}^{2}} = \frac{4^2}{5^2}$

⇒ $\frac{r_{1}}{r_{2}}  = \frac{4}{5}$

Now, let C₁ and C₂ be the circumference of two circles. Then,

C₁ = 2 π r₁ and C₂ = 2 π r₂

Therefore,

$\frac{C_1}{C_2} = \frac{2πr_1}{2πr_2} = \frac{r_1}{r_2} = \frac{4}{5}$

Hence, the circumference of the two circles are in the ratio 4 : 5.

Key Facts and Summary

1. The amount of space covered by a flat surface or piece of land or an object is called its area.
2. The unit of area is a unit square. This is written as unit² such as cm², m² km² etc.
3. A circle is the set of all those points in a plane whose distance from the fixed point remains constant. The fixed point is called the centre of the circle and the constant distance is known as the radius of the circle. The line segment passing through the centre of a circle and having its endpoints on the circle is called the diameter of the circle.
4. The area of a circle having a radius ‘r’ = πr² where π = $\frac{22}{7}$ or 3.14 (approx.)
5. Area of a Semi-Circle = $\frac{1}{2}$ ( Area of the circle ) = $\frac{1}{2}$πr²
6. The area of a sector is the region enclosed by the two radii of a circle and the arc. In simple words, the area of a sector is a fraction of the area of the circle.
7. Area of a sector when the central angle is given in degrees = ( $\frac{θ}{360}$) π r², where θ= central angle in degrees, and r = radius of the sector. 
8. Area of a sector given the central angle in radians = $\frac{( θr^2)}{2}$, where θ = the measure of the central angle given in radians and r = radius of the sector
9. Area of a sector given the arc length = r $\frac{L}{2}$, where,  L = length of the arc and r = radius of the sector.

Recommended Worksheets

Measurement, Perimeter, and Area Problem Solving (World Habitat Day Themed) Math Worksheets
Area of a Circle (Home Decorations & Furniture Themed) Worksheets
Circumference of a Circle (Summer Party Themed) Worksheets