Introduction
Geometry is a fascinating field of mathematics that allows us to measure and understand the world around us in new and exciting ways. One such measurement is the surface area of a hemisphere, which is an essential concept for students to grasp. The surface area of a hemisphere will be thoroughly explained in this article.
Grade Appropriateness
The concept of surface area, including a hemisphere, is typically introduced in the 7th grade. However, it can be revisited and further explored in higher grades, particularly in high school Geometry and Calculus classes.
Math Domain
This topic falls under the domain of Geometry, which deals with the properties, measurement, and relationships of points, lines, angles, surfaces, and solids.
Applicable Common Core Standards
The Common Core Standards related to this topic are:
7.G.B.4: Know the formulas for the area and circumference of a circle and use them to solve problems; give an informal derivation of the relationship between the circumference and area of a circle.
7.G.B.6: Solve real-world and mathematical problems involving area, volume, and surface area of two- and three-dimensional objects composed of triangles, quadrilaterals, polygons, cubes, and right prisms.
Definition of the Topic
In simple terms, a hemisphere is half of a sphere. It is what you get when you cut a sphere right down the middle. The surface area of a hemisphere includes the area of its circular base and the area of the curved part (like the surface area of a sphere).
Key Concepts
Area = 3rπ2, where r is the hemisphere’s radius, is the formula for a hemisphere’s total surface area.
This formula is derived by adding the curved surface area of the hemisphere (2πr²) and the base area (πr²).
Discussion with Illustrative Examples
The total area of a three-dimensional object’s surface or exterior is known as surface area.
The word hemisphere has the prefix hemi, which came from the Greek term hēmi meaning “half.” So, the hemisphere means half of a sphere. A hemisphere is composed of a curved surface that is half of a sphere and a circular flat base.
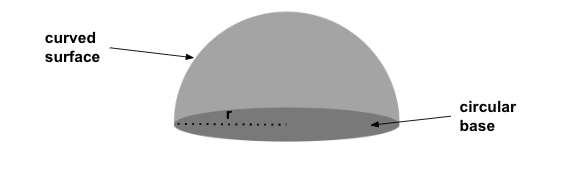
To get its total surface area, we need to add the area of its curved surface and the area of its circular base.
Formulas for Calculating the Surface Area of a Hemisphere
Curved Surface Area (C)
C = 2πr2
Circular Base Area (B)
B = πr2
Total Surface Area (T)
T = 3πr2
For these equations,
r = radius of the hemisphere
Remember that a hemisphere’s radius is a line drawn from the base’s center to any point on the curved surface.
Let us consider a hemisphere with a radius of 4 units.
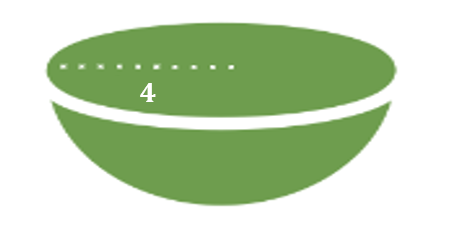
To find its total surface area, we plug the radius into the formula:
T=3πr2
T=(3)(π)(4)2
T=3π(16)
T=48π square units
Thus, the total surface area of the hemisphere is 48π square units.
Examples with Solution
Example 1
A hemisphere has a radius of 7 cm. What is its surface area?
Solution
T = 3πr2
T =(3)(π)(7 cm)2
T = 3π (49 cm2)
T=147π cm2
The total surface area is 147π cm2.
Example 2
Find the hemisphere’s total surface area and curved surface area with a radius of 8 m.
Use 3.14 as the estimated value of π.
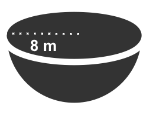
Solution
C=2πr²
C=(2)(3.14)(8 m)2
C=401.92 m2
T=3πr²
T=(3)(π)(8 m)2
T=602.88 m2
Therefore, the curved surface area is 401.92 m2, and the total surface area is 602.88 m2.
Example 3
Determine the curved surface area and total surface area of a hemisphere whose diameter is 51 cm. Use 3.14 as the estimated value of π.
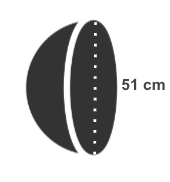
Solution
Since the radius is one-half of the diameter, the radius of the hemisphere is 51 ÷ 2 = 25.5 cm.
C = 2πr2
C =(2)(3.14)(25.5)2
C = 4 083.57 cm2
T = 3πr2
T =(3)(3.14)(25.5)2
T = 6 125.36 cm2
Therefore, the curved surface area is 4 083.57 cm2, and the total surface area is 6 125.36 cm2.
Example 4
A hemisphere has a surface area of 675π cm². What is its radius?
Solution
We rearrange the formula to solve for r:
Surface Area = 3πr²
r=$\sqrt{\frac{Surface Area}{3π}}$
r=$\sqrt{\frac{675π}{3π}}$
r=$\sqrt{225}$
r=15
Thus, the radius of the hemisphere is 15 cm.
Real-life Application with Solution
Mario is working on his mini globe hemisphere project has a radius of 50 centimeters. What is the surface area of the hemisphere? Use π =3.14.
Solution
T = 3πr2
T =(3)(3.14)(50)2
T = 23550
Therefore, the surface area of the mini globe hemisphere project is 23550 cm2.
Practice Test
A. Complete the table below. Use 3.14 as the value of π and round off your answers to the nearest hundredths.

B. Answer the following problem.
1. A hemispherical cake has a diameter of 11 inches. Calculate its total surface area.
2. Find the surface area of a hemisphere with a radius of 10 cm.
3. A hemisphere has a surface area of 100π cm². What is its radius?
4. If the surface area of a hemisphere is 500π m², what is the radius?
5. Calculate the surface area of a hemisphere with a radius of 5 m.
Answers:
A.
1. Radius = 4 cm, Curved Surface Area = 100.48 cm2, Total Surface Area = 150.72 cm2.
2. Radius = 7 m, Curved Surface Area = 307.72 m2, Total Surface Area = 461.58 m2.
3. Radius = 5.5 cm, Curved Surface Area = 189.97 cm2, Total Surface Area = 284.96 cm2.
B.
1. Total Surface Area = 90.75π square inches
2. Total Surface Area = 300π square centimeters
3. Radius ≈ 5.77 cm.
4. Radius ≈ 12.91 m.
5. Total Surface Area = 75π m².
Frequently Asked Questions (FAQs)
Do spheres and hemispheres have the same surface area?
No, the surface area of a hemisphere is half of a sphere’s surface area plus the area of the base of the hemisphere, which is a circle.
How is the formula for the surface area of a hemisphere derived?
The formula for a hemisphere’s surface area is created by adding the hemisphere’s curved surface area, which is 2πr², and the area of the circular base, which is πr². Hence, the formula for a hemisphere’s surface area results in 3πr².
Does the surface area of a hemisphere include the base?
Yes, the total surface area of a hemisphere includes both the curved surface area and the base area.
How does the radius of a hemisphere affect its surface area?
The surface area of a hemisphere is directly proportional to the square of its radius. If the radius doubles, the surface area increases by a factor of four.
What are some real-world applications of calculating the surface area of a hemisphere?
There are many real-world applications, such as calculating the amount of materials necessary to create a dome, the surface area of a planet (which is a sphere, but the concept is similar), or the area of a dome that needs to be painted, as in our example.
Recommended Worksheets
Surface Area of a Hemisphere (Halloween themed) Math Worksheets
Lateral Area of a Hemisphere (Rio Carnival Themed) Math Worksheets
Surface Area of a Sphere (Songkran Festival Themed) Math Worksheets









