Area of a Triangle

Triangles

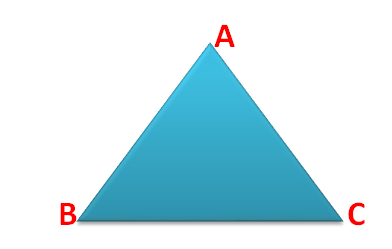
The word triangle is made from two words – “tri” which means three and “angle”. Hence, a triangle can be defined as a closed figure that has three vertices, three sides, and three angles. The following figure illustrates a triangle ABC:

Area of a Triangle

A triangle is a polygon that is made of three edges and three vertices. The vertices join together to make three sides of a triangle. The area occupied between these three sides is called the area of a triangle.

Formula for finding Area of a Triangle

General Formula

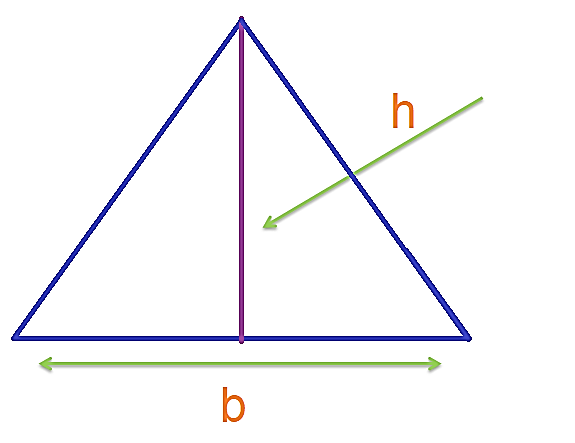
In general, the area of a triangle is defined by 1/2 x b x h

Area of a triangle = 1/2 x b x h

where b = base of the triangle (or any one side of the triangle), and  

H = Height of the triangle from that base (or side)

The following figure illustrates the base and the height of a triangle

The above formula is applicable irrespective of the fact whether a triangle is a scalene triangle ( having different sides), an isosceles triangle ( having two sides equal), or an equilateral triangle ( having all sides equal).

Let us understand this more through an example. Suppose we have a triangle that has one side as 6 cm and an altitude (height) of 8 cm on that base as shown in the following figure:

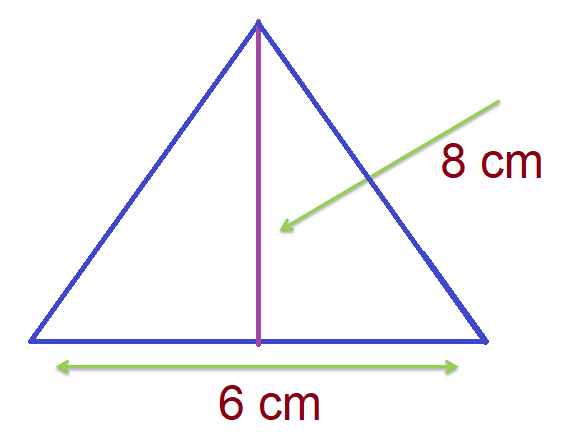
The area of this triangle is given by

 1/2 x b x h

Where b = 6 cm and h = 8 cm

Therefore, Area = 1/2 x 6 x 8 = 24 cm²

Area of a Right angled Triangle

Before learning about the area of a right angled triangle, we must first understand, what do we mean by a right angled triangle?

A triangle is said to be a right angled triangle if one of the angles of the triangle is a right angle, i.e. 90^o. Suppose, we have a triangle, ABC where △ABC = 90^o.  Then such a triangle is called a right angled triangle which would be of a shape similar to the below figure.

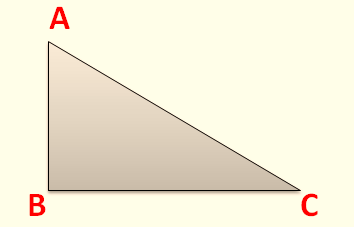
From the above image, it can be seen that a right angled triangle has a defined altitude in the form of the side AB and the side BC is its base. Hence the area of a right angled triangle can be calculated using the general formula only, which is given by

Area of a triangle = 1/2 x b x h

where b = base of the triangle, and h = Height of the triangle from that base (or side)

Area of an Equilateral Triangle

Before learning about the area of an equilateral triangle, we must first understand, what do we mean by an equilateral triangle?

A triangle is said to be an equilateral triangle if all its sides are equal. Also, if all the three sides are equal in a triangle, the three angles are equal.

The area of an equilateral triangle can be calculated using the general formula as stated above. But, can we calculate the area of an equilateral triangle if we know all the three sides but not the altitude? Let us find out

Let ABC be an equilateral triangle each of whose side is ‘a’ units in length. Let AD⟂ BC. Graphically, we represent this triangle as

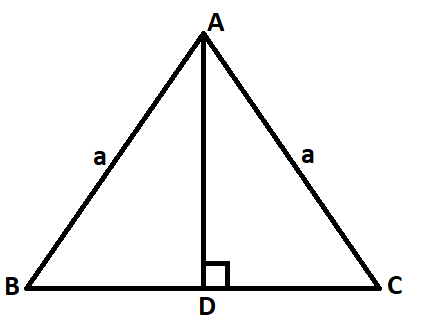
Then BD = DC = a/2

Applying Pythagoras theorem in ∆ABD, we have

AB² = AD² + BD²

⇒ AD = $\sqrt{AB^{2}-BD^{2}}$

⇒ AD = $\sqrt{a^{2}-\frac{a^{2}}{4}} = \sqrt{\frac{3a^{2}}{4}} =\frac{\sqrt{3a}}{2}$ units

Therefore, area of ∆ABC = 1/2 x (Base x Height)

Area of ∆ABC = 1/2 x BC x AD

Area of ∆ABC = $(\frac{1}{2} \times a \times \frac{\sqrt{3a}}{2})$ sq. units

 =[ $\frac{\sqrt{3}}{4}$ x (Side)² ] sq. units

This area of an equilateral triangle =[ $\frac{\sqrt{3}}{4}$ x (Side)² ] sq. units

Area of an Isosceles Triangle

Before learning about the area of an isosceles triangle, we must first understand, what do we mean by an isosceles triangle?

A triangle is said to be an Isosceles triangle if its two sides are equal. If two sides are equal, then the angles opposite to these sides are also equal.

For example, in the following triangle, AB = AC. Therefore ∆ABC is an Isosceles triangle.

∠B = ∠C

The area of an isosceles triangle can be calculated using the general formula as stated above. But, can we calculate the area of an isosceles triangle if we know the two equal sides and the base? Let us find out.

Let ABC be an isosceles triangle such that AB = AC = b units and BC = a units

Draw AD ⟂ BC

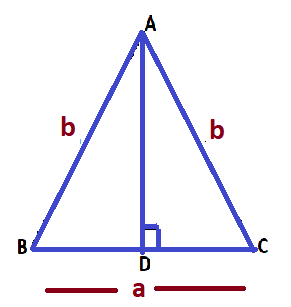
Then BD = DC = a/2

Applying Pythagoras theorem in ∆ABD, we have

AB² = AD² + BD²

⇒ b² = $AD^{2}+(\frac{a}{2})^{2}$

⇒ AD² = $b^{2}-\frac{a^{2}}{4}$

⇒ AD = $\sqrt{b^{2}-\frac{a^{2}}{4}}$

Therefore, area of ∆ABC = 1/2 x BC x AD

⇒ Area of ∆ABC = $\frac{1}{2} \times a \times \sqrt{b^{2}-\frac{a^{2}}{4}}= \frac{1}{2} \times Base \times \sqrt{(Equal\,Side)^{2}-\frac{1}{4}(Base)^{2}}$

Hence, the area of an isosceles triangle = $\frac{1}{2} \times Base \times \sqrt{(Equal\,Side)^{2}-\frac{1}{4}(Base)^{2}}$

Solved Examples

Example 1    

The area of a right triangle is 50 m2. If one of the sides is 20 m, find the height of the other side.

Solution: In the area of a right angled triangle, if one side is the base, then the other side is its altitude or height.

We have been given that one of the sides is 20 m. Let this be the base (b) of the triangle.

We know that area of a triangle = 1/2 x b x h

The area of the triangle has been given as 50 m²

Now,

50 = 1/2 x 20 x h

50 = 10 x h

h = 50/10  = 5 cm

Hence, the height of the triangle is 5 m

Example 2    

Find the area of an isosceles triangle having the base 6 cm and the length of each equal side 5 cm.

Solution: We know that

The area of an isosceles triangle = $\frac{1}{2}\times Base\times\sqrt{(Equal\,Side)^{2}-\frac{1}{4}(Base)^{2}}$

We have been given that the Base of the triangle = 6 cm and the length of each equal side 5 cm

Putting the values of the base and the equal sides in the formula for calculating the area we get,

The area of an isosceles triangle =  $\frac{1}{2}\times 6\times \sqrt{(5)^{2}-\frac{1}{4}(6)^{2}}$

=  $\frac{1}{2} \times 6 \times \sqrt{25-\frac{1}{4}\times 36}$

=  $\frac{1}{2} \times 6 \times \sqrt{25-9}$

=  $\frac{1}{2}\times6\times\sqrt{16}$

= $\frac{1}{2}\times 6\times\ 4$

= 12 cm²

Hence, the area of the given isosceles triangle = 12 cm²

Example 3    

A field is in the form of a triangle with hypotenuse 100 m and one side equal to 60 m. find the area of the field.

Solution: In order to find the area of the field we need to know the third side of the triangle. We have been given that the hypotenuse of the field is 100 m on one side equal is to 60 m. This means the field is a right angled triangle. Now, we know that in a right angled triangle one of the angles of the triangle is 90^o and the sides that make the right angle are called the base and the perpendicular while the third side is called the hypotenuse.

Therefore, according to the Pythagoras theorem, in a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides. Hence,

Base² + Perpendicular² = Hypotenuse²

Now, let the side that is given be the base of the triangle.

This means that Base (b) = 60 m. We have,

60² + Perpendicular² = 100²

⇒ 3600 + Perpendicular² = 10000

⇒ Perpendicular² = 10000 – 3600 = 6400

⇒ Perpendicular² = (80)²

Hence, perpendicular = 80 m.

Now that we know the base as well as the perpendicular, the area of the triangle is given by –

Area of a triangle = 1/2 x b x h

Area of a triangle = 1/2 x 60 x 80 m²

 Area of a triangle = 2400 m²

Hence, the area of the given triangle is 2400 m²

Example 4    

The base of a triangle is 5 units less than twice the height. If the area is 75 square units, then what are the length of the base and the height?

Solution: Let the height of the triangle be “h”. We have been given that the base of the triangle is 5 units less than twice the height. This means that the base (b) of the triangle will be:

b = 2h – 5

Now, we have also been given that the area is 75 square units. We know that the area of the triangle is defined by the formula:

Area of a triangle = 1/2 x b x h

This means that 1/2 x b x h = 75

Hence, b x h = 75 x 2 = 150

Placing the values of b and h we have in the above formula, we get:

(2h – 5) x h = 150

⇒ 2h² – 5h = 150

⇒ 2h² – 5h – 150 = 0

⇒ 2h² – 20h + 15h – 150 = 0 (Solving quadratic equation)

⇒ (2h² – 20h) + (15h – 150) = 0

⇒ 2h(h – 10) + 15(h – 10) = 0

⇒ (2h + 15)(h – 10) = 0

⇒h = -15/2 or 10 units

We know that the height of a triangle cannot be negative. Therefore the value -15/2 cannot be considered. This leaves us with the only value which is 10. Hence we can say that h = 10

Now that we know the value of h, we can find out the value of b.

Hence,

b = 2h – 5

b = 2 x 10 – 5 = 15 units

Therefore, the height of the triangle is 10 units while the base of the triangle is 15 units.

Note: We can check here that the value of base obtained is 15 which is 5 units less than twice the height of the triangle. Also if we put the values of the base and height in the formula for calculating the area of the triangle, we will get the area as 75 sq. units, which shows that our solution is correct.

Example 5    

Serena needs to order a shade for a triangular-shaped window that has a base of 6 feet and a height of 4 feet. What is the area of the shade?

Solution: We have been given that the base of the triangular-shaped window that Serena needs to order a shade for = 6 ft.

Also, the height of the triangular-shaped window that Serena needs to order a shade for = 4ft.

We are required to calculate the area of this shade. Since the shade is for a triangular-shaped window, we will use the formula for calculating the area of a triangle.

We have,

Area of a triangle = 1/2 x b x h

Therefore,

Area of a triangle = 1/2 x 4 x 6

Area of a triangle = 12 ft²

Hence, the area of the shade = 12 ft²

Example 6    

The area of a triangle is equal to that of a square whose each side measures 60 metres. Find the side of the triangle whose corresponding altitude is 90 metres.

Solution: We have been given that the area of a triangle is equal to that of a square whose each side measures 60 metres. Now, we know that area of a square is given by:

Area of a square = Side x Side

Therefore,

Now, that the side of the square is 60 metres, therefore,

Area of the square = 60 x 60 m²

Area of the square = 3600 m²

According to the question, this is also the area of the triangle. Hence,

Area of the triangle = 3600 m²

Now, we know that

Area of a triangle = 1/2 x b x h = 3600 m²

We have been given that the altitude of the triangle is 90 metres. Therefore, we need to find the base of the triangle.

Now,  1/2 x b x 90 = 3600 m²

⇒ b x 90 = 3600 x 2 = 7200 m²

⇒ b = 7200/90 = 80 m

Hence, the base of the triangle = 80 m

Example 7    

Find the area of an equilateral triangle having each side 4 cm.

Solution: We know that the area of an equilateral triangle is given by:

This area of an equilateral triangle =[ $\frac{\sqrt{3}}{4}\times$ (Side)² ] sq. units

Now have been given the side of the equilateral triangle as 4 cm. Putting the value of the side in the above formula we get,

 Area of the triangle =  [ $\frac{\sqrt{3}}{4}\times$ 4² ]

=  $\sqrt{3}\times4=4\sqrt{3}$ cm²

Hence, the area of an equilateral triangle having each side 4 cm = $4\sqrt{3}$  cm²

Example 8    

The base of an isosceles triangle is 12 cm and its perimeter is 32 cm. find the area of the triangle.

Solution : We have been given that,

The base of the isosceles triangle = 12 cm

The perimeter of the triangle = 32 cm

We know that the perimeter of a triangle = Sum of all its sides

Since the perimeter is equal to 32 cm and one of the sides is 12 cm, therefore, let the length of each of the two equal sides be “b”.

Therefore, we can say that

2b + 12 = 32

⇒ 2b = 32 – 12

⇒ 2b = 20

⇒ b = 10 cm

Hence, we now have that each of the equal sides measure 10 cm each.

Thus, now we have,

The base of the triangle = 12 cm

Equal side of the triangle = 10 cm each.

Now, we know that

Area of an isosceles triangle =  $\frac{1}{2}\times Base\times\sqrt{(Equal\,Side)^{2}-\frac{1}{4}(Base)^{2}}$

Putting the values of the base and the equal side in the above equation, we get:

Area of an isosceles triangle =  $\frac{1}{2}\times 12\times\sqrt{(10)^{2}-\frac{1}{4}(12)^{2}}$  

=  $\frac{1}{2}\times 12\times\sqrt{100-\frac{1}{4}\times144}$

=  $\frac{1}{2}\times 12\times\sqrt{100-36}$

= $6\times\sqrt{64}$

= 6 x 8

 = 48 cm²

Hence, the area of the given isosceles triangle = 48 cm²

Example 9    

Find the area in square centimeters of the triangle whose base = 1.5 m and altitude = 0.8 m.        

Solution: we have been given that

Base of the triangle = 1.5 m

Altitude of the triangle = 0.8 m

We know that

Area of a triangle =  x b x h

Therefore,

Area of a triangle = 1/2 x 1.5 x 0.8

= 1/2 x 1.5 x 0.4 = 0.6 m²

Now, note that we have been asked to find the area in square centimeters while the answer obtained above is in square meters. Therefore, we must convert this value into square meters.

The relation between square metres and square centimeters is defined as:

1 square meter = 10000 square centimeters

Therefore, 0.6 m² = 0.6 x 10000 = 60000 cm²

Hence, the area of the triangle in square centimeters = 60000 cm²

Recommended Worksheets

Scalene Triangles (Summer Camp Themed) Math Worksheets
Equilateral Triangles (Outer Space Themed) Math Worksheets
Isosceles Triangles (Holiday Cruise Ship Themed) Math Worksheets