What are Solid Shapes?
In order to understand vertices, edges and faces we first need to understand, what are solid shapes, also known as 3 Dimensional or 3 D shapes? Have you ever wondered about the shape of the matchbox or your laptop that so regularly use? What about the shapes of the ice-cream cone that is everyone favourite and the Pepsi can that the youngsters love to have? These are all 3 Dimensional or 3 D shapes. So, how do we define 3 D shapes? Let us find out.
3 Dimensional shapes or 3D shapes are the shapes that have all the three dimensions, i.e. length, breadth and height. These shapes are called solid shapes. In our everyday lives, we come across many solid shapes. For example, the laptop, our rooms, mobile phones, ice cream, tennis balls etc. are all examples of solid shapes. Let us understand some of these shapes in detail. But, before we look at the different solid shapes, we need to understand some common terms that are used to define different dimensions of solid shapes. So, here we have to define the 3D shapes are –
Polyhedron – A solid shape bounded by polygons is called a polyhedron. The word polyhedra are the plural of the word polyhedron. If the line segment joining any two points on the surface of a polyhedron entirely lies inside or out the polyhedron then it is called a convex polyhedron.
Now, let us learn about Vertices, Faces and Edges.
Face
Faces – Polygons forming a polyhedron are known as its faces. In other words, a face refers to any single flat surface of a 3D shape. For example, observe one side of your room or that of a Rubik’s cube. Every side has two dimensions, be it a length and a breadth, or a breadth and a height or a length and a height. Each side of a room forms its face.
Edge
Edges – Line segments common to intersecting faces of a polyhedron are known as its edges. In other words, an edge is a line segment on the boundary joining one vertex (corner point) to another. It is similar to the sides we have in 2D shapes.
Vertex
Vertices – Points of intersection of edges of a polyhedron are known as its vertices. In other words, the meeting point of a pair of sides of a polygon is called its vertex.
Let us now observe the vertices, faces and edges of different solid shapes.
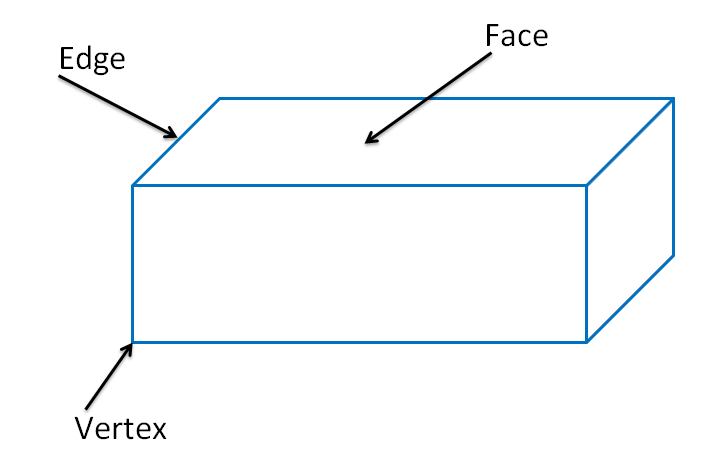
Cuboid
We know that a 3D shape having six rectangular faces is called a cuboid, for example, a matchbox, a brick, a book etc. In other words, it is an extension of a rectangle in a 3D plane. Other examples of cuboids include almirah, room, playing board box etc. a cuboid has length, breadth and height. Various parts of a cuboid are:
Faces: A cuboid has 6 rectangular faces. The opposite faces of a cuboid are identical.
Edges: Two adjacent faces of a cuboid meet in a line segment called an edge of the cuboid. A cuboid has 12 edges.
Vertex: Three edges of a cuboid meet at a point called a vertex. A cuboid has 8 vertices
Cube
A cuboid whose length, breadth and height are equal is called a cube. Examples of a cube are sugar cubes, cheese cubes and ice cubes. In other words, it is an extension of a square in a 3D plane.
Faces: A cube has 6 rectangular faces, out of which all are identical.
Edges: A cube has 12 edges
Vertex: A cube has 8 vertices

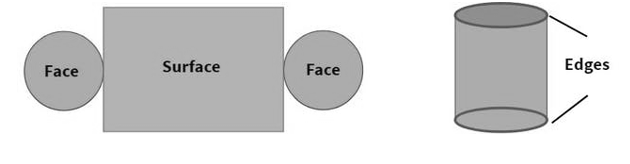
Cylinder
A cylinder is a solid with two congruent circles joined by a curved surface. Objects such as a circular pillar, a circular pipe, a test tube, a circular storage tank, a measuring jar, a gas cylinder, a circular powder tin etc. are all shapes of a cylinder. A cylinder has a curved lateral surface and two circular faces at its ends.
Faces: A cylinder has one curved surface and two flat faces. In other words, a cylinder has two plane faces, namely the top and the base and one curved face. The distance between the end faces of a cylinder is called its length.
Edges: A cylinder has two curved edges.
Vertex: A cylinder has no corner or vertex.
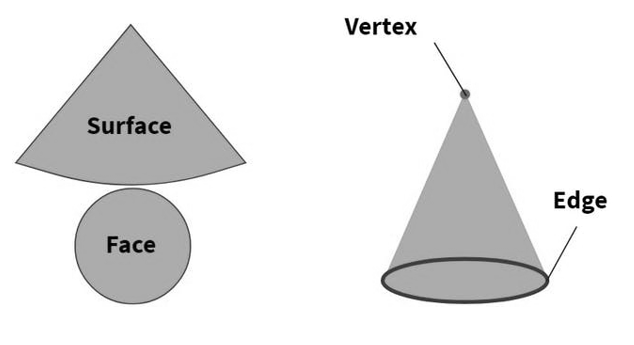
Cone
A circular cone has a circular base that is connected by a curved surface to its vertex. A cone is called a right circular cone if the line from its vertex to the centre of the base is perpendicular to the base. An ice-cream cone is an example of a cone
Faces: A cone has one flat face and one curved surface.
Edges: A cone has one curved edge.
Vertex: A cone has one vertex.
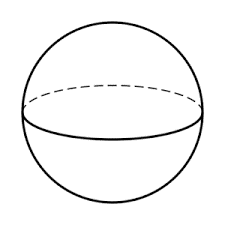
Sphere
A sphere is a solid formed by all those points in space that are at the same distance from a fixed point called the centre. In other words, it is an extension of a circle in a 3D plane.
Faces: A cone has one curved surface.
Edges: A cone has no edge.
Vertex: A cone has no vertex.
Platonic Solids
A platonic solid is a polyhedron. It is interesting as well as surprising to know that there are exactly five platonic solids. Tetrahedron. These five platonic solids are tetrahedron, cube, octahedron, icosahedron, and dodecahedron.
Note that in any polyhedron, at least three polygons (called faces) must meet at the vertex to form a solid angle. Also, the sum of all the plane angles forming the solid angle at a vertex must be less than that of 360o. Let us start with the simplest regular polygon forming the face of a polyhedron. Clearly, such a regular polygon is an equilateral triangle. Let us now understand about these five platonic solids and their vertices, edges and faces.
Tetrahedron
Polyhedron or metallic solid whose faces are congruent equilateral Triangles is called the tetrahedron. A unique property of the tetrahedron is that all four vertices are the same distance from each other.
A tetrahedron has:
- 4 triangular faces, i.e. F = 4
- 4 vertices, i.e. V = 4
- 6 edges, i.e. E = 6
Hexahedron
Let us now move to the next regular polygon that is square. Six squares form a cube. Cube is the only platonic solid whose every face is a square. Cube is also known as a hexahedron as it has six squares as its faces.

A cube (hexahedron) has:
- 6 square faces, i.e. F = 6
- 8 vertices, i.e. V = 8
- 12 edges, i.e. E = 12
Tetrahedron and cube are platonic solids in which three faces ( regular polygons ) meet at a point to form a vertex.
Octahedron
Let us now move on to a new platonic solid in which four regular polygons meet at a point to form a vertex. The platonic solid which has four equilateral triangles meeting at each vertex is known as the octahedron.
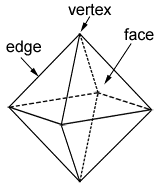
An octahedron has:
- 8 triangular faces, i.e. F = 8
- 6 vertices, i.e. V = 6
- 12 edges, i.e. E = 12
Icosahedron
The platonic solid in which five equilateral triangles meet at a point to form a vertex is known as an icosahedron.
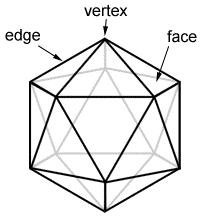
An icosahedron has:
- 20 triangular faces, i.e. F = 20
- 12 vertices, i.e. V = 12
- 30 edges, i.e. E = 30
Dodecahedron
Now, we have learnt about platonic solids having their faces as equilateral triangles and squares. Let us now discuss about platonic solids whose every face is a pentagon. This platonic solid is known as the Dodecahedron. In a Dodecahedron, three pentagons meet at every vertex.
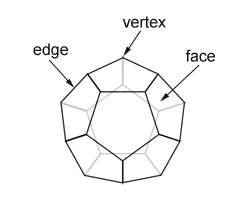
A dodecahedron has:
- 12 triangular faces, i.e. F = 12
- 20 vertices, i.e. V = 20
- 30 edges, i.e. E = 30
Relationships between the Vertices, Edges and Faces of Platonic Solids
In order to understand the relationship between the Vertices, Edges and Faces of Platonic Solids. We place the information in the below table.
| Platonic Solid | Faces | Edges | Vertices |
| Tetrahedron | 4 | 6 | 4 |
| Cube | 6 | 12 | 8 |
| Octahedron | 8 | 12 | 6 |
| Icosahedron | 12 | 30 | 20 |
| Dodecahedron | 20 | 30 | 12 |
Relationship between Tetrahedron and a Cube
From the above table, we can see that 6 edges in a tetrahedron = 6 faces in a cube
This is because of the fact that a tetrahedron can be inscribed in a cube. Each of the 6 edges of the tetrahedron can serve as the diagonals of one of the 6 faces of the cube.
Next, we have
Relationship between Tetrahedron and Itself
From the above table, we can see that 4 faces in a tetrahedron = 4 vertices in a tetrahedron
This is because; every face is directly opposite a vertex in a tetrahedron. Hence, there is a one-to-one relation between faces and vertices. So, if there are four vertices in one, there have to be four faces in the other.
Another characteristic of the tetrahedron is that it can be superimposed with a copy of itself facing in the opposite direction.
Now, we come to the relationship between the faces and vertices of an octahedron.
Relationship between Tetrahedron and Octahedron
From the above table, we can see that 6 edges in a tetrahedron = 6 vertices in an octahedron
This is primarily because an octahedron can be inscribed in a tetrahedron. Also, relationships between vertices, faces and the edges in the cube and the octahedron can be defined as –
Relationship between Cube and Octahedron
From the above table, we can see that 6 faces in a cube = 6 vertices in an octahedron
8 vertices in a cube = 8 faces in an octahedron
12 edges in a cube = 12 edges in an octahedron
Do you that there is a name given to this peculiar relation between the cube and the octahedron? This special triple relationship between the cube and the octahedron is called duality.
Relationship between Cube and Dodecahedron
From the above table, we can see that 12 edges in a cube = 12 faces in a dodecahedron
This is primarily because of the fact that a cube can be inscribed in a dodecahedron.
Relationship between Cube and Icosahedron
From the above table, we can see that 12 edges in a cube = 12 vertices in an icosahedron
Relationship between Octahedron and Icosahedron
From the above table, we can see that 12 edges in an octahedron = 12 vertices in an icosahedron
This is possible because an icosahedron is inscribed in an octahedron.
Relationship between Octahedron and Dodecahedron
From the above table, we can see that
12 faces of dodecahedron = 12 vertices of icosahedron
20 vertices of dodecahedron = 20 faces of icosahedron
30 edges of dodecahedron = 30 edges of icosahedron
Again, a triple relationship of duality is present between an octahedron and a dodecahedron.
Also, from the table, we can infer that
12 edges in an octahedron = 12 faces in a dodecahedron
Euler’s Formula
Now that we have learnt about the vertices, edges and faces, can we define a relation between them? Let us find out.
Leonhard Euler (1707-1783) was a Swiss mathematician who was one of the greatest and most productive mathematicians of all time. He spent much of his career blind, but still, with the help of scribes, he wrote one paper per week. Euler gave one very popular formula called Euler’s polyhedral formula. So, what was this formula proposed by Euler that defined the relationship between the vertices, edges and the faces of a polyhedron? Let us find out.
According to Euler,
The number of faces (F), the number of vertices (V) and the number of edges (E), of a simple convex polyhedron are connected by the following formula:
F + V = E + 2
This is called Euler’s formula.
Euler’s Formula does work only for a polyhedron with certain rules. The rule is that the shape should not have any holes, and also it must not intersect itself. Also, it cannot be made up of two pieces stuck together, like two cubes stuck together by one vertex.
If all of these rules are properly followed, then this formula will work for all polyhedrons. Thus this formula will work for most of the common polyhedral.
There are in fact many shapes that produce a different answer to the sum FE. The answer to the sum FE is sometimes called the Euler Characteristic X.
Solved Examples
Harry is aware of the fact that a polyhedron has 12 vertices and 30 edges. How can he find the number of faces?
Solution
We will use the Euler’s formula to find the polyhedron.
We know that, according to Euler’s formula, the number of faces (F), the number of vertices (V) and the number of edges (E), of a simple convex polyhedron are connected by the following formula:
F + V = E + 2
Now, we have been given that Harry is aware of the fact that a polyhedron has 12 vertices and 30 edges
This means that here,
V = 12
E = 30
Putting these values in the Euler’s formula we get.
F + 12 = 30 + 2
⇒ F + 12 = 32
⇒ F = 32 – 12 =20
Hence, the number of faces of the polyhedron = 20
Verify the Euler’s formula for a tetrahedron
Solution
We know that a tetrahedron has:
4 triangular faces, i.e. F = 4
4 vertices, i.e. V = 4
6 edges, i.e. E = 6
We also know that, according to Euler’s formula, the number of faces (F), the number of vertices (V) and the number of edges (E), of a simple convex polyhedron are connected by the following formula:
F + V = E + 2
Now, putting the values of F, V and E in the above equation, we have:
L.H.S
F + V
= 4 + 4 = 8 …………………………… (1 )
R.H.S
E + 2
= 6 + 2 = 8 ………………………………… (2 )
We can see that ( 1 ) = ( 2 )
Hence, we can say that Euler’s formula is verified for a tetrahedron.
Remember
- Polygons forming a polyhedron are known as their faces.
- An edge is a line segment on the boundary joining one vertex (corner point) to another.
- Points of intersection of edges of a polyhedron are known as its vertices. In other words, the meeting point of a pair of sides of a polygon is called its vertex.
- There are five platonic solids, namely, tetrahedron, cube, octahedron, icosahedron, and dodecahedron.
- Euler’s formula states that the number of faces (F), the number of vertices (V) and the number of edges (E), of a simple convex polyhedron are connected by the following formula: F + V = E + 2
- The number of edges, vertices and faces of different shapes is:
| Shape | Faces | Edges | Vertices |
| Cuboid | 6 | 12 | 8 |
| Cube | 6 | 12 | 8 |
| Cylinder | 3 | 2 | 0 |
| Cone | 2 | 1 | 1 |
| Sphere | 1 | 0 | 0 |
| Tetrahedron | 4 | 6 | 4 |
| Octahedron | 8 | 12 | 6 |
| Icosahedron | 12 | 30 | 20 |
| Dodecahedron | 20 | 30 | 12 |
Recommended Worksheets
2-D and 3-D Shapes Kindergarten Math Worksheets
Identifying Triangles, Quadrilaterals, Pentagons, Hexagons, and Cubes 2nd Grade Math Worksheets
Drawing And Describing 2D And 3D Figures 7th Grade Math Worksheets









