Introduction
Welcome, young learners! We will delve into a fascinating part of math – calculating the area of irregular shapes. Do you recall our lessons on finding the area of rectangles, triangles, and circles? That’s right! We’re now moving one step ahead and will tackle shapes that don’t quite fit into those categories. These are called “irregular shapes”, and by the end of this guide, you’ll master how to find their areas. Let’s dive in!
Grade Appropriateness
Our journey through irregular shapes is suitable for students in grades 3 to 6. But don’t worry if you’re younger or older. Math is for everyone, and understanding how to work with irregular shapes can be a fun and useful skill at any age!
Math Domain
This topic comes under the Geometry domain in mathematics. Geometry deals with points, lines, shapes, and spaces. It’s how we understand the physical shapes and spaces around us. The area of irregular shapes is a particular aspect of geometry that focuses on figuring out the space that different shapes cover.
Applicable Common Core Standards
This topic of Area of Irregular Shapes directly connects to several Common Core Standards:
3.MD.C.7: Relate area to the operations of multiplication and addition.
4.MD.A.3: Apply the area and perimeter formulas for rectangles in real-world and mathematical problems.
6.G.A.1: Find the area of right triangles, other triangles, special quadrilaterals, and polygons by composing them into rectangles or decomposing them into triangles and other shapes.
Definition of the Topic
An “irregular shape” in math is a shape that does not have a regular or standard definition. It could be a combination of rectangles, triangles, circles, or other shapes. The space a shape occupies, expressed in square units, is its area.
Key Concepts
Decomposition: This is the process of breaking down an irregular shape into recognizable shapes like rectangles, triangles, and circles. We calculate their areas separately and then add them up.
Grid Method: This method involves counting the full and half squares on a grid that an irregular shape covers.
Discussion with Illustrative Examples
An irregular shape has angles of different sizes and sides of different lengths.
Compared to regular shapes, irregular shapes are often much harder to name because they don’t look like the more conventional regular shapes.
Differentiating Regular Shapes and Irregular Shapes
| Name | Regular | Irregular | Number of Sides |
| Triangle | 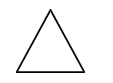 | 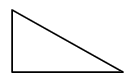 | 3 |
| Quadrilateral |  | 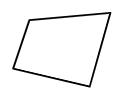 | 4 |
| Pentagon | 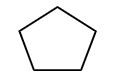 | 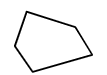 | 5 |
| Hexagon |  | 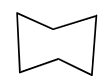 | 6 |
| Octagon | 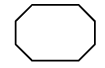 | 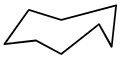 | 8 |
Notice how regular shapes differ from irregular shapes. Observe the sides of the shape as well as the angles.
Finding the Area of the Irregular Shapes
Divide the irregular shape into regular shapes you are familiar with, such as a rectangle, triangle, square, or circle, to calculate the area of irregular shapes.
Example:

We can now calculate the total area of the irregular shape by adding the regular shape areas that we obtained by dividing the irregular shape.

Area of Regular Shapes
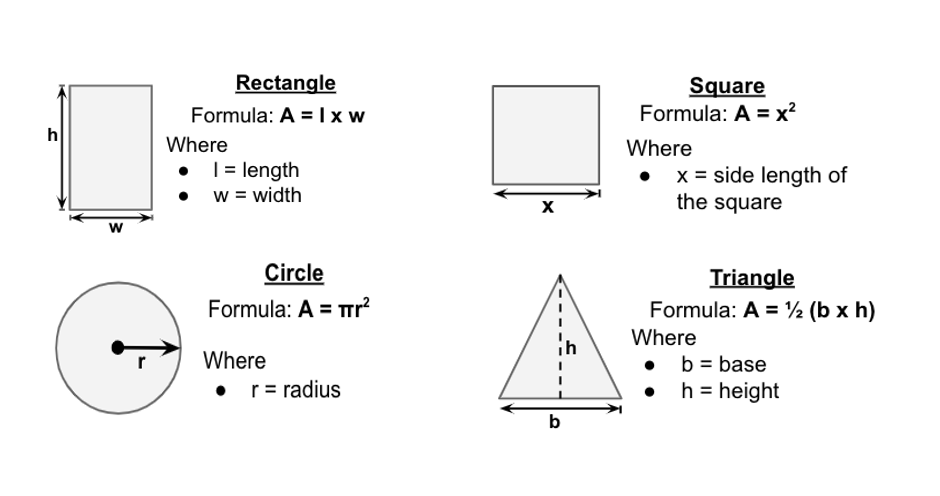
Examples with Solution
Example 1
Calculate the area of the irregular shape below.
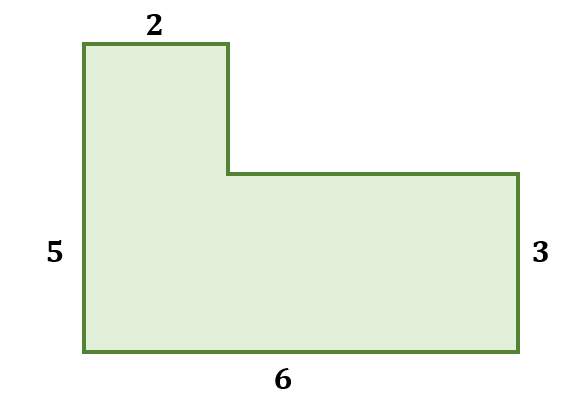
Solution

Decomposition Method:
You have an ‘L’ shape. The horizontal rectangle is 3 units wide and 4 units long, and the vertical rectangle is 2 units wide and 5 units long.
Horizontal Rectangle: 3 × 4 = 12 square units
Vertical Rectangle: 2 × 5 = 10 square units
Total Area: 12 + 10 = 22 square units
Grid Method:
Count all the squares that the irregular shape covers.
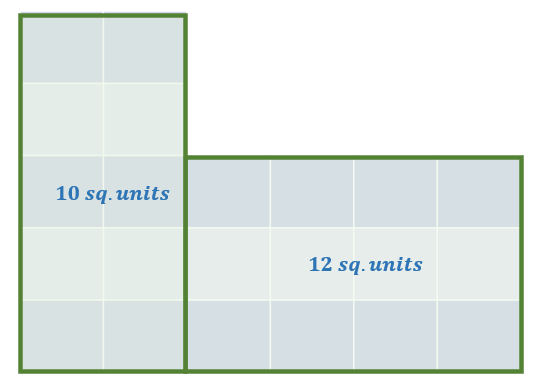
Hence, the total area of the irregular shape is 22 square units.
Example 2
You have a shape covering eight full squares and six half squares on a grid. Calculate the area.
Solution
Full squares: 8
Half squares: 6 * 0.5 = 3
Total Area: 8 + 3 = 11 square units
Example 3
Find the area of the irregular shape below.
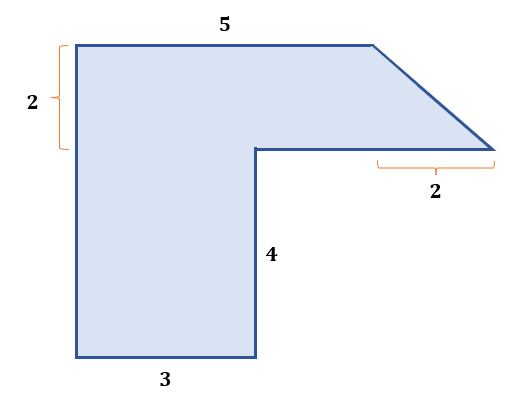
Solution
We can have these regular shapes if we divide the given figure.
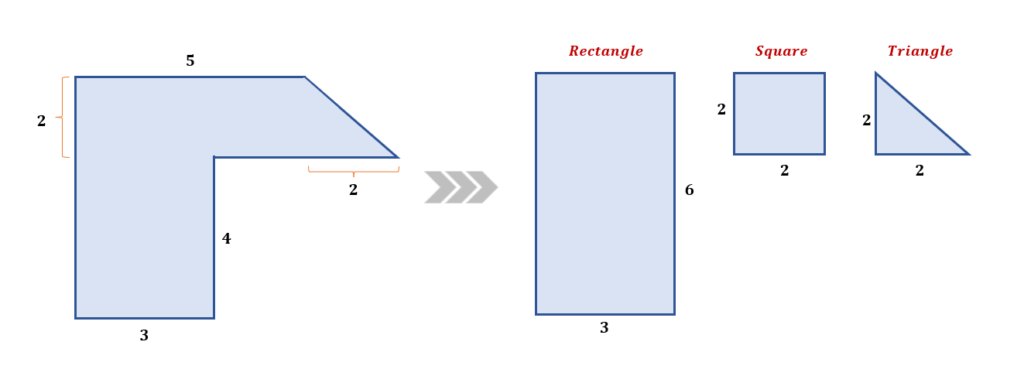
Decomposition method:
Rectangle: 6 × 3 = 18 square units
Square: 22 = 4 square units
Triangle: ½ × 2 × 2 = 2 square units
Total Area = 18 + 4 + 2 = 24 square units
Grid Method:
We must count all the squares that the irregular shape covers.
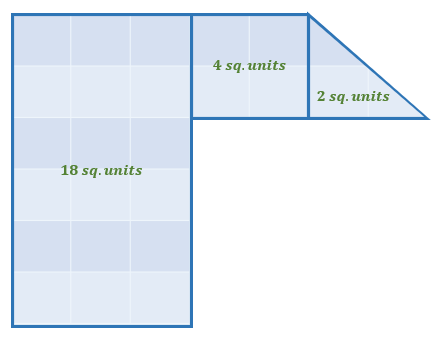
Thus, the irregular shape has a total area of 24 square units.
Real-life Application with Solution
Perhaps you’re thinking, “Why do I need to learn this?” Well, let’s look at a real-life example!
Imagine you’re helping your parents plant a garden. The garden bed has a funky shape – like a rectangle but with a triangular piece missing. The rectangular part is 4 feet wide and 5 feet long. The missing triangular part is a right-angled triangle with a base (b) of 2 feet and a height (h) of 3 feet.
To find out how much soil you need, you must know the area of the garden bed.
Area of the rectangle: 4 × 5 = 20 square feet
Area of the triangle: ½ × 2 × 3 = 3 square feet
Since the triangle is missing from the garden bed, you subtract its area from the rectangle’s area: 20 – 3 = 17 square feet. So, you need enough soil to cover 17 square feet!
Practice Test
Let’s test your knowledge! Remember to decompose the shapes if you can and use the grid method when necessary.
1. An irregular shape comprises a square with sides of 4 units and a rectangle with a width of 2 units and a length of 3 units. What’s the total area?
2. An irregular shape is made up of a rectangle with a width of 2 units and a length of 6 units and a triangle with a base (b) of 2 units and a height (h) of 3 units. What’s the total area?
3. An irregular shape covers a grid of 15 full squares and 4 half squares. What’s the total area?
4. An irregular shape covers 7 full squares and 8 half squares on a grid. What’s the total area?
5. An irregular shape is made up of a square with sides of 5 units, a rectangle with a width of 3 units and a length of 4 units, and a triangle with a base of 3 units and a height of 2 units. What’s the total area?
Answers:
1. 22 square units
2. 15 square units
3. 17 square units
4. 11 square units
5. 40 square units
Frequently Asked Questions (FAQs)
Can all irregular shapes be decomposed into regular shapes?
While not all irregular shapes can be perfectly decomposed into regular shapes, most can be approximated by a combination of regular shapes, which can help us estimate the area.
Why is it necessary to calculate the area of irregular shapes?
This skill is useful in many real-world applications, like planning a garden, calculating the paint needed for a wall, or designing a playground.
Is the grid method accurate for calculating the area?
The grid method provides an estimate rather than a precise measurement, especially when the shape doesn’t perfectly align with the grid. However, it is a helpful way to get an approximate idea of the area.
What if an irregular shape is composed of circles or parts of circles?
You can use the formula if an irregular shape includes circles or parts of circles.
Recommended Worksheets
Area of Irregular Shapes (Skills Themed) Math Worksheets
Regular and Irregular Shapes (World Oceans Day Themed) Math Worksheets
Symmetrical Shapes (Bodhi Day Themed) Math Worksheets









