Introduction
We know that the basic shapes of Geometry are squares, rectangles, circles and triangles, trapezoids, rhombuses, stars, hexagons, octagons, and ovals. By using any of two basic shapes we can make or construct a composite shape. If we have a composite shape that consists of a semi-circle attached to the side of a rectangle then we can also use multiple sections of basic shapes in the same composite shape. For example, we can make a kite shape by using a basic shape circle. For this, we can easily compose the circle into a kite shape then the shape that we will get from a circle which is a basic shape will produce a composite shape kite. Composite shapes are those shapes that are constructed from two or more geometric shapes. It may refer to any geometric shapes that can be sorted out to create more than one basic shapes that exist in Geometry. Some examples of basic shapes to form the composite shapes are square and triangle, triangles and circles, etc. In other words, A composite shape is a geometrical shape that is the combination of many common geometrical shapes. Let’s learn about composite shapes in detail in this section.
Definition
A shape that can be divided into more than one of the basic shapes like circle, square, triangles, stars and ovals etc, is said to be a composite shape.
The composite shape is a shape in which different shapes are put together to form a required shape that will be a Unique and defined shape as well. These shapes can be made up of a combination of triangles, squares, circles, etc. A composite shape is made up of basic geometric shapes by joining them with each other.
Let us learn about composite shapes and how they can be determined. A composite shape is also called a compound shape is one that consists of multiple different geometric shapes.
For example,
Below are some shapes that represent the concept of composite shapes.
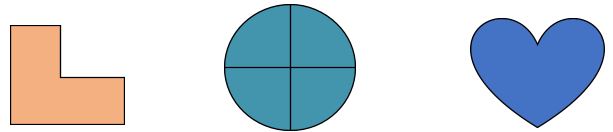
We can see that in shape 1 if we cut the shape into two pieces we will get one rectangle and one square. It means that this is a composite shape that consists of two basic geometrical shapes rectangle and square.
For shape 2, which is a composite shape because when we cut the given shape into four parts we will get four cones. For shape 3, if we cut the shape into pieces we will get two semi-circles and one square. It means that this is a composite shape that consists of two basic geometrical shapes circle and square.
Perimeter of composite shapes
The perimeter of a shape is the complete estimate of all the edges of a shape e.g. a square has four edges, so its perimeter is the total of those four edges added together. The perimeter of a square is easy to calculate if one side is given as all sides are the same length because we know that in the square we have all equal sides in length; the perimeter of a square with a side length of 3cm is 12 cm because 3 x 4 = 12
We can find the area of composite shapes by finding the area of the basic geometric shapes that make it and then adding them with each other.
In some perimeter problems, the lengths of some of the sides may be unknown. Let’s look at this fact through example
Sometimes we need to work out the lengths of sides that have not been given in the composite shapes to us. If a composite shape has unknown sides, then the first thing to do is to find them out by comparing them to other sides of the given Composite shape.
Here is an example of a composite shape with unknown side lengths x and y.
For example : We have a rectangular composite shape with two unknown side lengths then find its perimeter?
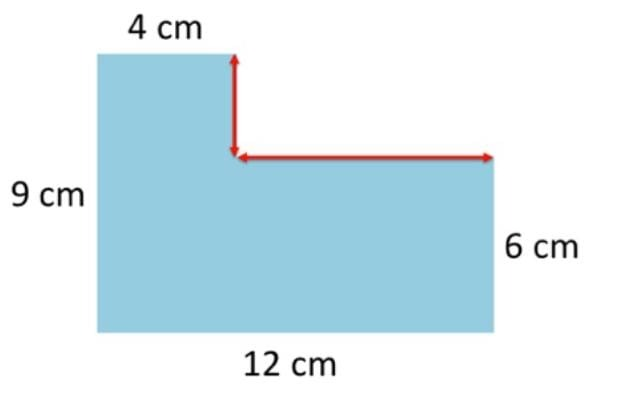
Solution :
First, we calculate the value of x which is vertical length. we know that the side is 9 cm long is equal to
X plus the side which is 6 cm long .so,
X = 9 – 6 = 3
Hence the value of x is 3 cm.
We will find the value of y is given composite shape, we know that the whole horizontal length is 12 cm long which is equal to the sum of y, and the side length 4 cm long.
So,
Y = 12 – 4 = 8
Hence the value of y is 8 cm.
For the perimeter of composite shape we will add all sides length of given composite shape so,
Perimeter of composite shape = 4 + 3 + 6 + 8 + 12 + 9 = 42
Hence the perimeter of given composite shape is 42 cm.
Area of Composite Shapes
The area of composite shapes is a combination of basic geometric shapes like circles, squares, triangles, stars, ovals, etc. To divide any composite shape, we must know to calculate the area of some basic shapes like squares, triangles, rectangles, ovals, etc. Let’s learn more about the area of composite shapes through the example
For example : Given composite shape is made of two rectangles. Find the area of Composite Shapes?
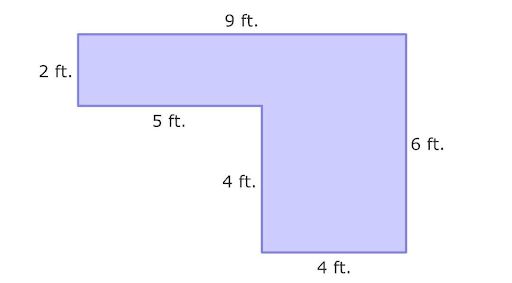
Solution :
We know that a given shape is composite, first, we will divide it into Basic geometric shapes. For this, we draw a line to divide the composite shape into basic shapes. So, we have
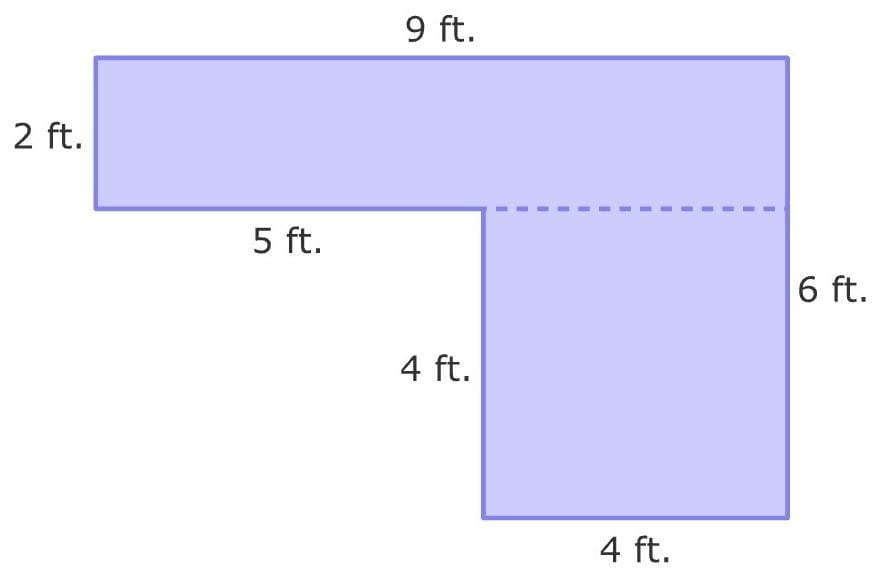
Now we have two rectangles. We will find the area of each rectangle by multiplying length and width
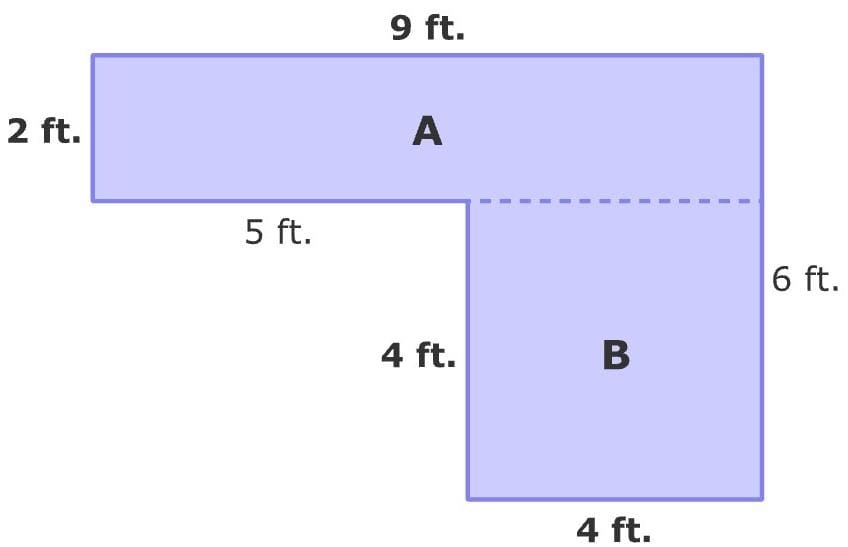
For rectangle A, We have length l=2 ft and width w=9 ft
Area of Rectangle A=length ×width
Area of Rectangle A= 2 × 9
Area of Rectangle A = 18 square feet
Now for rectangle B,
We have length l=4 ft and width w=4 ft
Area of Rectangle B=length ×width
Area of Rectangle B= 4 × 4
Area of Rectangle B = 16 square feet
The last step is to add the areas of both the basic shapes.
Total Area =18+ 16 =34
So, the area of the composite shape is 34 square feet!
How to measure
We have some steps to find the area of a composite shape
1: Divide the composite shape into basic geometric shapes.
2: Find the area of every basic geometric shape separately.
3: Add all the areas of basic geometric shapes with each other. 4: Write the answer in square units.
Additive area method
In the additive area method of composite shapes, we first divide the composite shapes into basic geometric shapes then find their area separately. After this, we add the area of these basic geometrical shapes to find the area of composite shapes. For example, If we have a rectangle that is in composite shape because we can divide it into two triangles then we will find the area of these triangles to get the area of composite shapes.
Subtractive area method
In case of subtraction the area of the composite shape will be the difference between the area of the larger shape and the areas of the parts of the larger shape but not included in the composite shape.
We can find the area of composite shapes either by additive method or subtractive method but you will prefer additive method if you will use perimeter to find area of composite shapes.
Volume of Composite Shapes
To find the volume of composite shapes, we need to identify the different parts it is made of. This partition allows working out the volume of each part independently. The volume of the composite shape is simply the sum of the volumes of its parts or composing shape Volume. For composite prisms, where the bases are a composite shape, the area of the bases is the sum of the areas of the parts it is made of. The volume of the composite prism is then given by multiplying the base area by the height of the prism.
Let’s learn about the volume of composite shapes through some examples.
For example, Find the volume of the given composite shape?
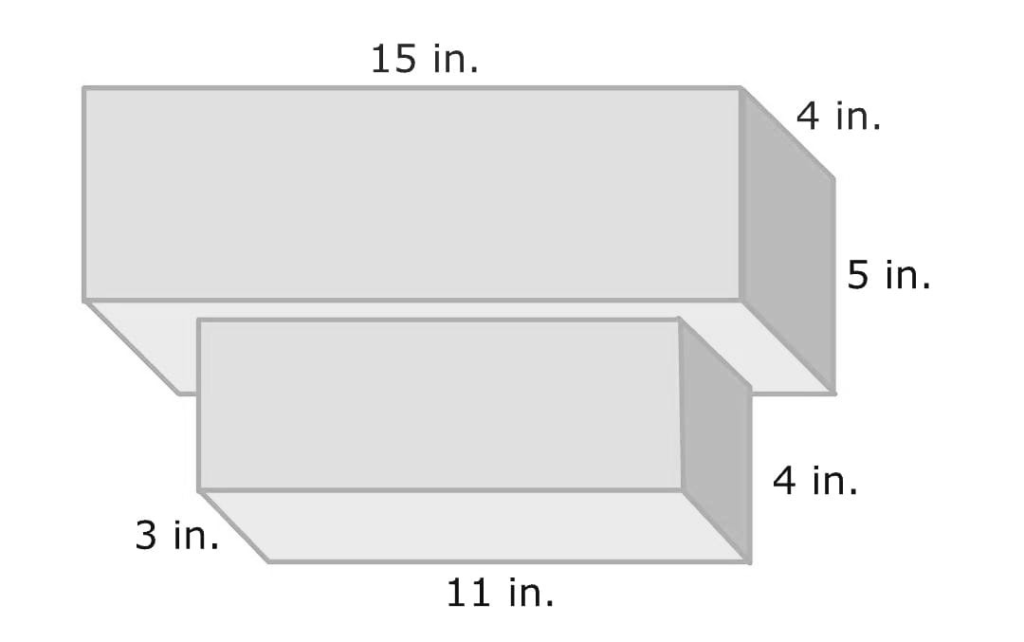
Solution :
Given shape is rectangular prism and we know that formula for the volume of a rectangular prism is:
Volume is the product of length, width, and height
So,
V = l × w × h
( Where l is the length, w is the width and h is the height of the prism ) To find the volume of a given composite shape we will divide the shape into two parts rectangular prisms
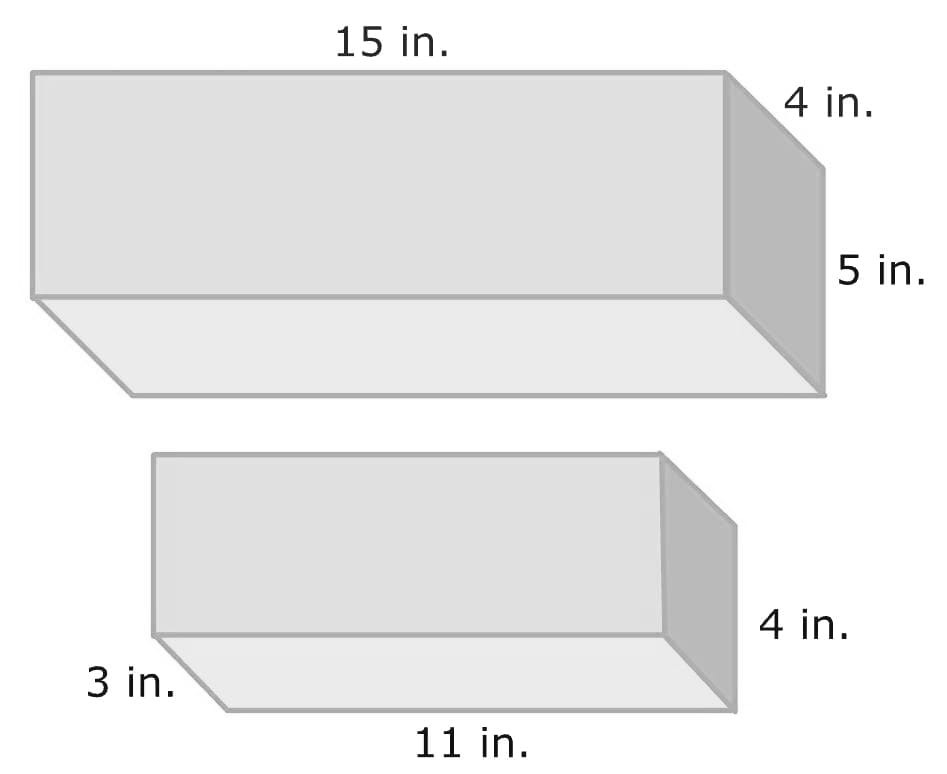
Now, we will find the volume of each prism. First, we will find the volume of a large prism

We know that from shape length is 15 inches, width is 4 inches, and height is 5 inches.
Now by the formula of volume
V = l × w × h
V = 15 × 4 × 5
V = 300
Hence, the volume of the large prism is 300 cubic inches.
Next, we will find the volume of the small prism
We know that from shape length is 11 inches, width is 3 inches, and height is 4 inches.
Now by the formula of volume
V = l × w × h
V = 11 × 3 × 4
V = 132
Hence, the volume of the large prism is 132 cubic inches.
To find the total volume of the given shape, we will add the volumes of large and small prisms.
V = 300+132 = 432
The volume of the shape is 432 cubic inches.
How to measure
We have some steps to find the volume of a composite shape.
1: Divide the composite shape into basic geometric shapes.
2: Find the volume of every basic geometric shape separately.
3: Add all the volume of basic geometric shapes with each other.
4: Write the answer in cube units.
Solved Examples :
Example 1 : Find the perimeter and area of the given composite shape?
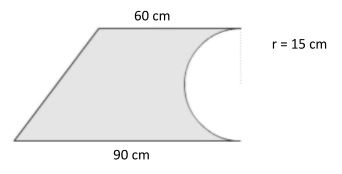
Solution :
To find the perimeter of composite shapes we will add the lengths of the sides. For finding the value of unknown x first, we know that the radius of the semicircle is 20 cm, the distance between the 60 cm and 90 cm sides is 40 cm. The hypotenuse of the right triangle can be found by substituting the known lengths of 40cm and 40 cm into the formula for the Pythagorean theorem. The length of the semicircle x can be found by multiplying the circumference formula for a circle by one-half which is given in the first shape.
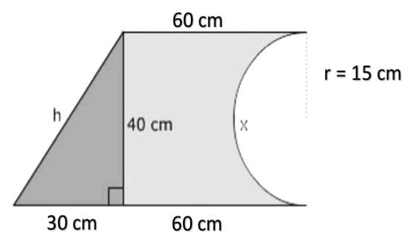
For total length, by Pythagorean theorem
h2 = (30)2 + (40)2
h2 =(900)2 + (1600)2
h2 = (2500)2
Taking square root from both sides
h = 50 cm
For value of x,
X = $\frac{1}{2}$ × circumference of circle
X = $\frac{1}{2}$ × 2πr
We know that
circumference of circle=2πr
x = πr
Putting the value of r in above formula
x = 15 π cm
Now perimeter will be equal to some of all outside edges, so
P = 50 + 60 +80 + 15 π
P= 237.123
Hence, the perimeter of the given composite shape is 237.123 cm
Now we will find the area of the Composite shape.
For this first, we will calculate the area of the Right triangle.
We know that area of the Right triangle is equal to
A = 1/2 ×base × altitude
Putting the values of base and altitude in the above formula, we will get the area of the Right triangle.
A = 1/2 × 30× 40
A= 600 cm²
Secondly, we will calculate the area of the Rectangle.
We know that area of the Rectangle is equal to
A = Lenght × width
Putting the values of length and width in the above formula, we will get the area of the Rectangle
A = 60 × 40
A= 2400 cm²
Now, we will calculate the area of the semicircle.
We know that area of the semicircle is equal to
A = 1/2 π × r²
A= 1/2 × 3.1415 × (15)²
A= 353.42 cm²
We have calculated the Area of the Right triangle, rectangle, and semicircle. Now we will add this area by the additive method of the area of composite shapes to get the area of composite shapes so,
Area of Composite shape = 600+2400+353.42
Area of Composite Shape = 3353.42 cm ² Hence, the area of composite shape will be 3353.42 cm²
Example 2 :
What is the area of given composite shape?
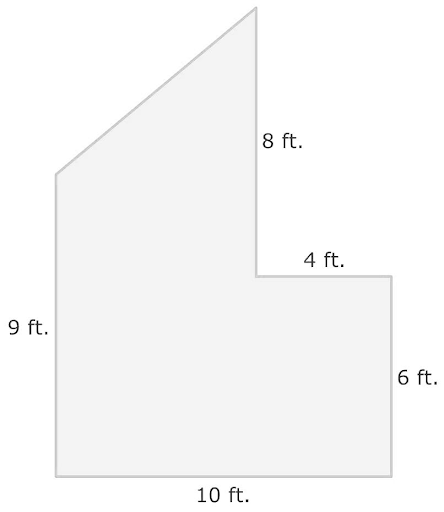
Solution :
For the area of composite shapes, first, we will divide this composite shape into Basic geometric shapes so, we can show that by figure
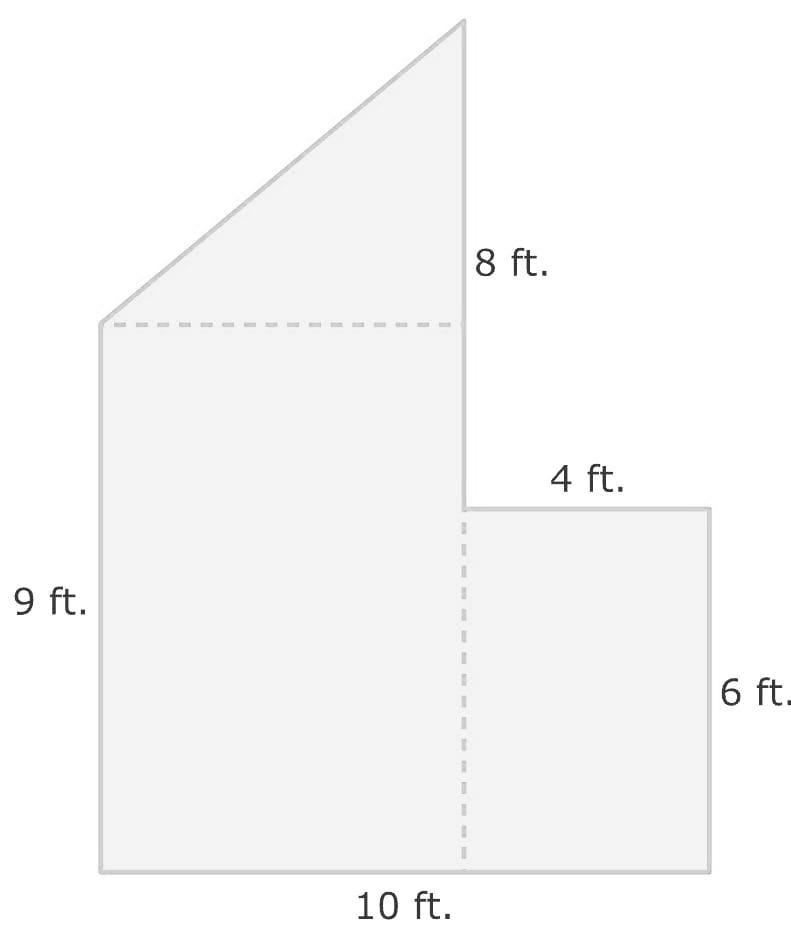
We have divided the given composite shape into two rectangles and one right triangle.
Firstly, we will find the area of the Right triangle.
From shape A, we know that base is 6 and 5 in height
So,
Area of right triangle is = $\frac{1}{2}$ base × height
Area of shape A= $\frac{1}{2}$ × 6 × 5 = 15
Hence, the area of the right triangle is 15 ft²
Secondly, we have rectangle B, for this, we have length 6 and width 9
So the area of rectangle B will be
Area of Rectangle B= 9×6
Area of Rectangle B= 54
Hence, the area of Rectangle B is 54 ft²
Now, we have the last rectangle C, for this, we have length 4 and width 6
So the area of rectangle C will be
Area of Rectangle C= 4×6
Area of Rectangle C= 24
Hence, the area of Rectangle C is 24 ft²
To find the area of composite shape, we will add the area of basic geometric shapes Rectangle B, Rectangle C, and right triangle A.
Area of Composite shape= 15 +54+ 24
Area of Composite shape= 93 ft²
Hence, the area of composite shape will be 93 ft ².
Example 3 :
Find the volume of the given composite shape?
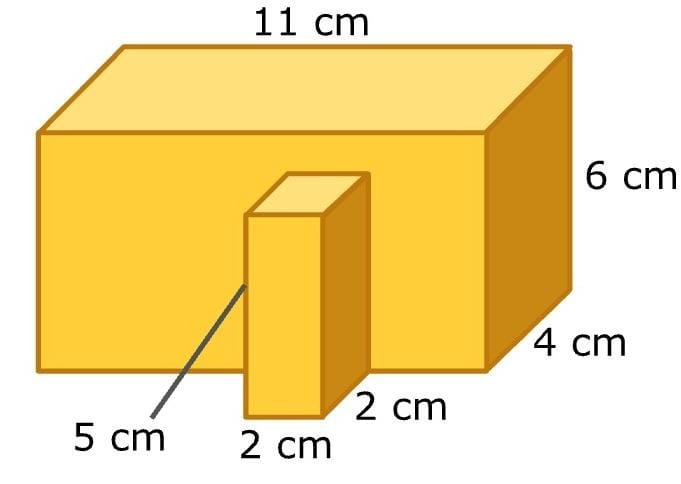
Solution :
Given shape is rectangular prism and we know that formula for the volume of a rectangular prism is:
Volume is the product of length, width, and height
So,
V = l × w × h
( Where l is the length, w is the width and h is the height of the prism ) To find the volume of a given composite shape we will divide the shape into two parts as rectangular prisms.
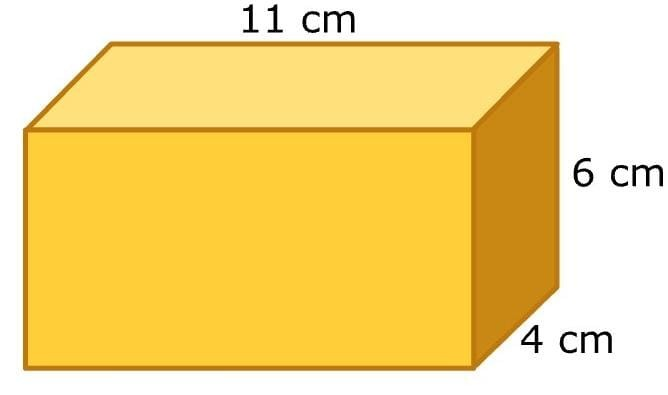
Now, find we will find the volume of each prism. First, we will find the volume of a large prism
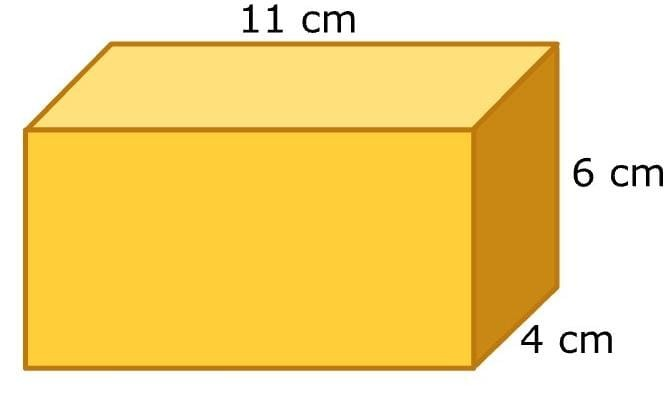
We know that from shape length is 11 centimeters, width is 4 centimeters, and height is 6 centimeters.
Now by formula of volume
V = l × w × h
V = 11 × 4 × 6
V = 264
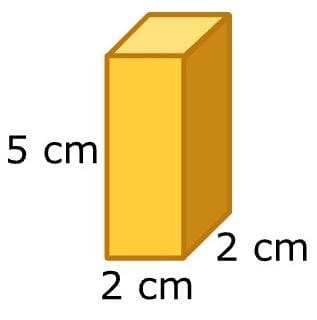
Hence, the volume of the large prism is 264 cubic centimeters. Next, we will find the volume of the small prism.
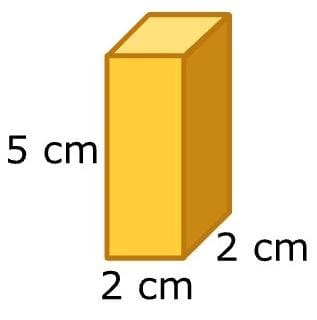
We know that from shape length is 2 centimeters, width is 2 centimeters, and height is 5 centimeters.
Now by formula of volume
V = l × w × h
V = 2 × 2 × 5
V = 20
Hence, the volume of the large prism is 20 cubic centimeters.
To find the total volume of the given shape, we will add the volumes of large and small prisms.
V = 264+20 = 284 The volume of the shape is 284 cubic centimetres.
Example 4:
Given composite shape below is made from five equal squares.
The area of a composite shape is 200 cm ²
Find the length of side Y?

Solution :
We know that a given composite shape has four sides and these sides are equal because the shape is square.
So the area of square= (sides )²
Put the 5 sides and Area value in the above formula
4 Y²=200
Y²= 50
By taking square root on both sides,
Y = 2√5
Hence, the side length of the given composite shape is 2√5
Example 5 :
What is the area of the composite shape?
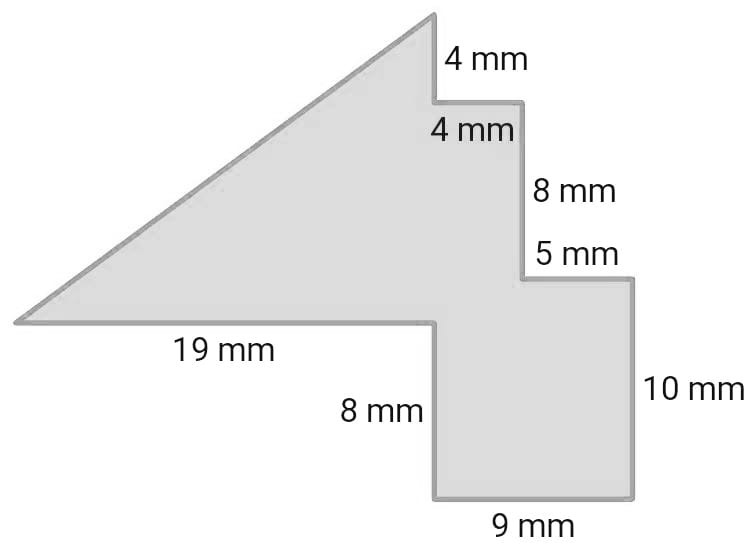
Solution :
We know that a given shape is composite, first, we will divide it into Basic geometric shapes. For this, we draw a line to divide the composite shape into basic shapes. So, we have
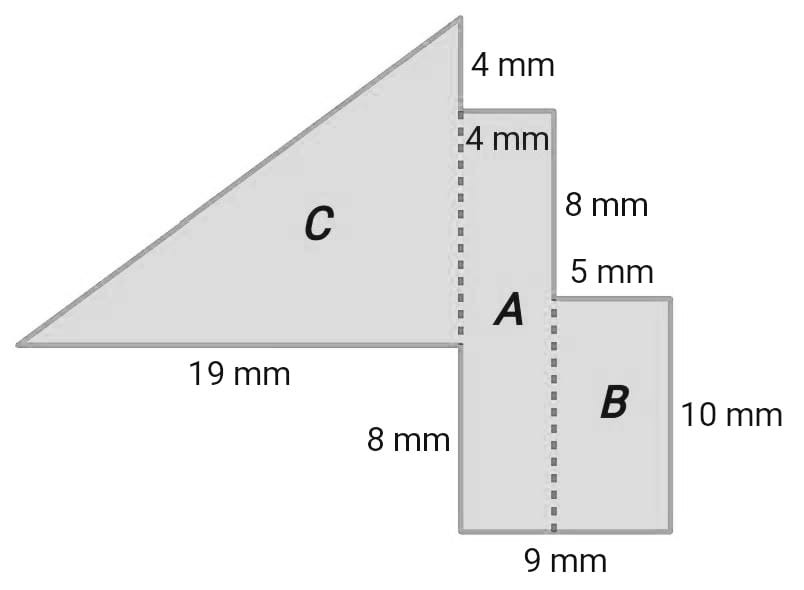
Now we have two rectangles and one triangle. We will find the area of each rectangle by multiplying length and width and the area of the triangle by multiplying base and width.
For rectangle A,
We have length l=4 mm and width w=18 mm
Area of Rectangle A=length ×width
Area of Rectangle A= 4 × 18
Area of Rectangle A = 72 mm2
Now for rectangle B,
We have length l=5 mm and width w=10 mm
Area of Rectangle B=length ×width
Area of Rectangle B= 5 × 10
Area of Rectangle B = 50 mm2
Lastly, we will find the area of the Right triangle.
From shape C, we know that base is 19 and 14 in height.
So,
Area of right triangle is = $\frac{1}{2}$ base × height
Area of shape C= $\frac{1}{2}$ × 19 × 14 = 133 mm²
Hence, area of right triangle is 133 mm²
Key Facts and Summary
- Composite shapes can be divided into more than one of the basic shapes like circles, square triangles, stars, ovals, etc.
- Area of Composite shape can be calculated by two methods i.e additive and subtractive method
- Composite shapes are those shapes that are constructed from two or more geometric shapes.
- We can measure the area and volume by following steps :
- By Dividing the composite shape into basic geometric shapes.
- By Finding the area and volume of every basic geometric shape separately.
- By Adding all the area and volume of basic geometric shapes with each other.
- If the dimensions of all the basic shapes are raised, the area of composite shapes also increases.
- The area of composite shape changes as it depends on the individual area of basic geometric shape which gets changed when the dimensions are increased or raised.
- There is no fixed formula to calculate the area of composite shapes.
- The perimeter of a shape is the complete estimate of all the edges of a shape e.g. a square has four edges, so its perimeter is the total of those four edges added together.
- If some values are unknown in composite shape then we have to find these values because from all outside edges, we can find the perimeter of the Composite shape.
Recommended Worksheets
Kinds of Shapes (Christmas Themed) Math Worksheets
Measurement, Perimeter, and Area Problem Solving (World Habitat Day Themed) Math Worksheets
Spatial Skills: Perimeter (Las Posadas Themed) Math Worksheets









