What is a Square?
A square is a quadrilateral that has four equal sides and four right angles. In other words, a square is a quadrilateral with the following properties:
- The opposite sides of a square are parallel
- All the four sides of the square are equal
- Al the four angles of a square measure 90o
- The diagonals of a square bisect each other at 90o
- The diagonals of a square are equal in length
How to calculate the area of a Square?
The amount of space covered by a flat surface or piece of land or an object is called its area. For a square whose side is of ‘s’ units:
Area of a Square = Side x Side = s2 sq. units
For example, if we have a square whose one side is 6 cm, its area would be calculated as
Area = Side x Side = 6 x 6 = 36 cm2
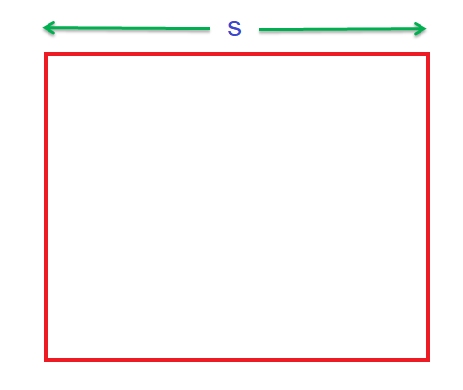
Finding the area of a square when we are given the Perimeter of a Square
We now know how to calculate the area of a square when the measurement of its side is given. But how do we get to know the area of a square when instead of the sides, we are given the perimeter of the square. Let us find out.
To find out the area of a square when we are given the Perimeter of a Square, we will proceed in two steps –
Step 1 – Finding the side of the square
We know the perimeter of a closed shape is the sum of all its sides. The square has 4 sides all of which are equal. Therefore, for a square of side “s” cm, the perimeter of the square will be
Perimeter of a Square =(s + s +s + s) cm = 4s cm
Hence,
Perimeter of a Square = 4 x Side
Now that we have been given the perimeter of the square, this means that the products of 4 and the side of the square will be equal to this perimeter.
Therefore, the length of one side of a square can be obtained by;
Side = $\frac{Perimeter}{4}$
Step2 – Finding the area of the Square
Now that we have the measurement of the side, we can easily calculate the area of a square by the general formula we have already learnt i.e.
Area of a Square = Side x Side = s2 sq. units
Let us understand this by an example.
Example: Find the area of a square park whose perimeter is 320 m
Solution: We have been given that the perimeter of the square park is 320 m.
We know that:
The perimeter of a Square = 4 x Side
Therefore,
320 = 4 x Side
⇒ Side = $\frac{320}{4}$ cm = 80 m
Hence, side of the square park = 80 m
Now, to find out the area of the square, we know that
Area of a Square = Side x Side = s2 sq. units
Therefore,
Area of a Square Park= (80 x 80) m2 = 6400 m2
Hence, the area of the square park = 6400 m2
Finding the area of a square when we are given the Diagonal of a Square
We now know how to find out the area of a square using its side or the perimeter. But, what if we don’t know either of them and still want to obtain the area of a square. There is a third important measurement in a square which is known as its diagonal. Let us find out how to calculate the area of a square when we just know the measurement of its diagonals.
In order to find the area, we must first plot the diagonals in a square as shown in the following diagram:
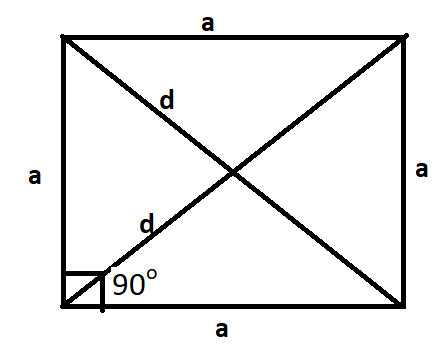
So, let us have a square with each side as “a” cm and each diagonal as “d” cm.
We know that all the four angles of a square measure 90o
We also have the Pythagoras theorem that states that For a right-angled triangle,
Hypotenuse2 = Perpendicular2 + Base2
Hence, we can say that a2 + a2 = d2
⇒ 2a2 = d2
⇒a2 = $\frac{d^{2}}{2}$ ……………………………….. (1)
Now, we also know that area of a square with side:
a = a2………………………………(2)
From (1) and (2), we have
Area of a square = $\frac{d^{2}}{2}$
Hence, we can say that the area of a square having diagonal (d) = $\frac{d^{2}}{2}$
Let us understand it through an example
Example: Find the area of a square land a diagonal of length 10 m.
Solution: We have been given that the diagonal of the square land = 10 m
We know that area of a square having diagonal (d) = $\frac{d^{2}}{2}$
Hence,
Area of the square land = $\frac{10^{2}}{2}$ m2 = $\frac{100}{2}$ m2 = 50 m2
Hence, the area of a square land a diagonal of length 10 m = 50 m2



Examples
Example 1
Find the area of a square whose diagonal length is 16 cm
Solution: We have been given that the diagonal length of the square is 16 cm.
To find the area of the square, we need to use the relation between the side and the diagonal of the square using the diagonal.
Let the side of the square be “p” cm.
Now, we know that
Area of a Square = (Side)2 = p2
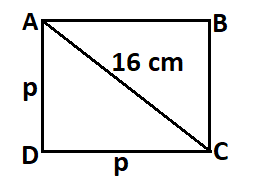
Using Pythagoras theorem, we have,
= (Side)2 + = (Side)2 = (Hypotenuse)2
⇒ p2 + p2 = (16)2
⇒ 2 p2 = 256
⇒ p2 = 128
Hence, area of the triangle = 128 cm2
Example 2
A rectangular park and a square mall have the same perimeter of 100 m. If the rectangular park has a breadth 2 m less than that of the square mall, find
a) the breadth of the rectangular park
b) the length of the rectangular park
c) the area of the rectangular park
Solution:
a) We have been given that the rectangular park and the square mall have the same perimeter. We know that all sides of a square are equal and the perimeter of a square = 4 x Side.
Therefore, we can say that
4 x Side = 100 m
Side = \frac{100}{4} = 25 m
Hence, the side of the square = 25 m.
We have also been given that the rectangular park has a breadth 2 cm less than that of the square mall. This means that the breadth of the rectangular park = 25 – 2 = 23 m.
Hence, breadth of the rectangular park = 23 m
b) Now, we need to find the length of the rectangular park. We now know the breadth of the rectangular park and its perimeter, since the rectangular park and the square mall have the same perimeter. We also know that
Perimeter of a rectangle = 2 (Length + Breadth)
Therefore,
2 (Length + 23) = 100 m
2 x Length + 46 = 100 m
2 x Length = (100 – 46) m
2 x Length = 54 m
Length = $\frac{54}{2}$ m = 27 m
Hence, length of the rectangular park = 27 m
c) Next, we need to find the area of the rectangular park. From the previous calculations, we have both the length and the breadth of the rectangular park, i.e.
Length of the rectangular park = 27 m
Breadth of the rectangular park = 23 m
We know that,
Area of the rectangle = Length x Breadth
Therefore,
Area of the rectangular garden = (27 x 23) m2 = 621 m2
Area of the rectangular park = 621 m2
Example 3
How many square metres of glass will be required for a window that has 12 panes each pane measuring 25 cm by 25 cm?
Solution: We have been given that each pane of the glass measures 25 cm by 25 cm. we need to find out how many square metres of glass will be required for a window that has 12 such panes.
To find this, we first need to find the area of one pane. Since both the dimensions of the pane are the same, it is a square. So, we use the formula for calculating the area of a square to find out the area of each pane.
We know that
Area of a Square = Side x Side = s2 sq. units
Side of one square glass pane = 25 cm
Note: We need to find out the glass required in square metres. Hence, we change our dimensions from cm to m.
Since, 1 m = 100 cm, therefore
25 cm = 0.25 m
Now, Area of one square glass pane = (0.25 x 0.25) m2 = 0.625 m2
We have 12 panes in all. Therefore, an area of 12 panes is the total square metres of glass panes required.
Hence, area of 12 square glass panes = (0.625 x 12) m2 = 0.75 m2
Therefore,
For a window that has 12 panes each pane measuring 25 cm by 25 cm, we will need 0.75 m2 of glass.
Example 4
Maria has a square plot with the measurement as shown in the figure. She wants to construct a house in the middle of the plot. A garden is developed around the house. Find the total cost of developing a garden around the house at the rate of £55 per square metres.
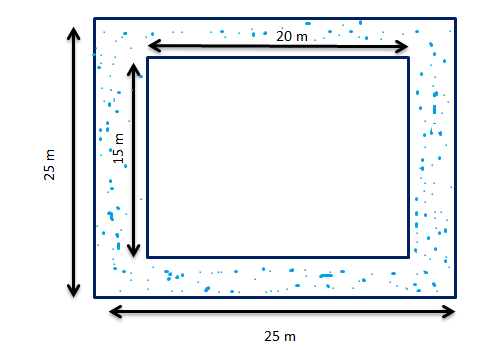
Solution: We have been given that the square plot that Maria has, is of the dimensions 25 m by 25 m
We need to find the cost of developing a garden around the house at the rate of £55 per square metre. For this, we need to calculate the area of the garden. We can see that the garden area is between the square plot and the house. This means that the area covered by the garden is equal to the difference between the area of the plot and the house.
Therefore,
Area of the garden = Area of the plot – Area of the house………………………. (1)
Let us first find the area of the plot. Since the plot is square in shape, we will use the formula for calculating the area of the square. We know that
Area of a Square = Side x Side = s2 sq. units
One side of the plot = 25 m
Area of the square plot = (25 x 25) m2 = 625 m2…………………………….. (2)
Now, Length of the house = 20 m
Breadth of the house = 15 m
Area of the house = Length x Breadth = (20 x 15) m2 = 300 m2…………………….. (3)
Now, putting the values obtained from (2) and (3) in (1), we get
Area of the garden = (625 – 300) m2 = 325m2
Now that we know the area of the garden and we have been given that the total cost of developing a garden around the house at the rate of £55 per square metres, therefore,
Cost of developing 1 square metre of the garden = £55
Cost of developing 325 square metres of the garden = £(55 x 325) = £17875
Hence, the total cost of developing a garden around the house at the rate of £55 per square metre = £17875
Example 5
In exchange for a square plot of land one of whose sides is 84 m a man wants to buy a rectangular plot 144 m long and of the same area as the square plot. Find the width of the rectangular plot.
Solution: We have been given that the area of the square plot of land and the rectangular plot that the man wants to buy is the same. Therefore,
Area of the square plot of land = Area of the rectangular plot
Now, area of the square plot of land = Side x Side = (84 x 84) m2 = 7056 m2 ………………………….. (1)
Also, area of the rectangular piece of land = Length x Breadth = 7056 m2
We have been given that the length of the rectangular plot = 144 m
Therefore,
7056 = 144 x Breadth
Breadth = $\frac{7056}{144}$ = 49 m
Therefore, the breadth / width of the rectangular piece of land = 49 m
Example 6
A square park of side 60 m and a rectangular park of side 80 m have the same perimeter. Which park has a larger area?
Solution: We have been given that a square park of side 60 m and a rectangular park of side 8 m have the same perimeter. To check which park has the larger area we need to first calculate the area of both the parks. Let us check if we have all the information to calculate the area of the two parks.
The area of a square park = Side x Side
So, the only dimension we need to calculate the area of a square park is its side, which is given as 60 m
The area of the rectangular park = Length x Breadth
But, we have been given just one dimension of the rectangular park. Therefore, we need to find out the second dimension. For this purpose, we shall use the given condition that the perimeter of both the parks is the same.
Therefore,
Perimeter of square park = 4 x Side = 4 x 60 = 240 m
Now, the perimeter of the rectangular park should also 240 m
Also, Perimeter of the rectangular park = 2 (Length + Breadth)
Therefore,
2 (Length + Breadth) = 240
Length + Breadth = $\frac{240}{2}$ = 120 m ……………………………. (2)
We take the one given dimension as its length.
Hence length of the rectangular park = 80 m
Now, putting this value in (2) we have,
80 + Breadth = 120
Breadth = 120 – 80 = 40
Hence, breadth of the rectangular park = 40 m
Now we have all the required dimensions to calculate the area of both the parks,
Therefore,
Area of the square park = (60 x 60) m2 = 3600 m2 ………………………………. (3)
Area of the rectangular park = (80 x 40) m2 = 3200 m2 ………………………………. (4)
From (3) and (4), we can see that
3600 > 3200
Therefore,
The area of the square park is more than the area of the rectangular park.
Example 7
Find the area in square centimetres of a square whose side 2.4 dm
Solution: We have been given that side of the square = 2.4 dm
We know that
Area of a Square = Side x Side = s2 sq. units
But, before calculating the area we must first check the units we have been given in the question and the units in which the area is required to be calculated.
The side is given in dm while the area is required in cm2. Hence, we should first convert 2.4 dm into centimetres.
We know that,
1 dm = 10 cm
Therefore, 2.4 dm = 2.4 x 10 = 24 cm
Now, area of the square = (24 x 24) cm2 = 576 cm2
Hence, area of a square whose side 2.4 dm is 576 cm2
Example 8
Find the area in square centimetres of a square whose side 20 mm
Solution: We have been given that side of the square = 20 mm
We know that
Area of a Square = Side x Side = s2 sq. units
But, before calculating the area we must first check the units we have been given in the question and the units in which the area is required to be calculated.
The side is given in mm while the area is required in cm2. Hence, we should first convert mm into centimetres.
We know that,
10 mm = 1 cm
Therefore, 20 mm = 2 cm
Now, area of the square = ( 2 x 2 ) cm2 = 4 cm2
Hence, area of a square whose side 20 mm is 4 cm2
Recommended Worksheets
Measuring Area Using Square Grids (Painting Themed) Worksheets
Area of Squares and Rectangles (Real Estates Themed) Worksheets
Area of Other Quadrilaterals (Province Themed) Math Worksheets









