Attributes of Shapes

What is an attribute?

The characteristics of a shape or a specific object are referred to as its “attributes.” It is how you visually and mathematically describe something. 

Say, for instance, that some characteristics of these pillows, such as their style, quality, length, and weight, can be used to describe them. Based on their color, we may say that we have pillows with blue-and-white stripes and pillows with red-and-white stripes. 

These items likewise have red and white and blue and white stripes, but they are umbrellas rather than pillows. Although they could have a character with the pillows up top, these are different things.

Shapes may also have comparable or identical characteristics, although this does not necessarily imply that it is that shape. The shape that is being given can be defined and categorized by specific characteristics.

In the world around us, we can see different two-dimensional ( 2D ) and three-dimensional ( 3D ) basic shapes. Their attributes give details that describe the shape presented. We can categorize shapes by understanding their characteristics or attributes. The attributes of shapes will have greater emphasis in this article.

Defining and Non-Defining Attributes of Shapes

Let us try to analyze the shapes to the right. These shapes have attributes that can be used to define them. These shapes are both medium in size, green-white, and orange, but are they the same shape?

Defining attributes are distinguishing characteristics of shapes. They must be closed figures with certain number of sides, corners, or vertices. For us to define a shape, certain characteristics of the shape must exist or be true. 

Non-defining attributes do not always apply to the shape. The color, size, pattern, direction, and orientation of a shape can all vary. A shape might be small or large depending on its size. Additionally, shapes can come in a variety of colors; some are yellow, some are blue, some are red, and some come in other colors. Shapes can also have patterns; some feature dots, stripes, or other design elements.

There are defining and non-defining attributes when analyzing shapes. Let us examine the following table:

Defining Attributes	Non-Defining Attributes	Defining Attributes	Non-Defining Attributes
Number of Sides: Four (4 ), same length Number of corners or vertices: Four ( 4 ) It is a closed figure.	Color: Green and white Size:  medium Pattern: Striped	Number of Sides: Three (3)  Number of corners or vertices: Three ( 3 ) It is a closed figure.	Color: Orange Size:  medium Pattern: Dotted

Describing 2D Shapes

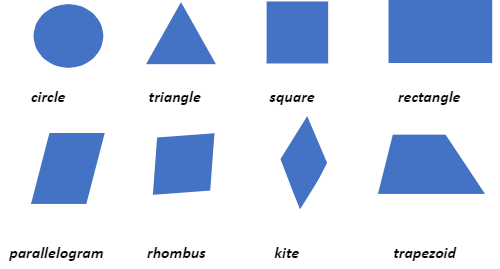
Two-dimensional (2D) shapes are flat shapes that lack thickness or height. They just have the length and width as dimensions. Some examples of 2D shapes include circles and polygons like triangles, squares, rectangles, etcetera.

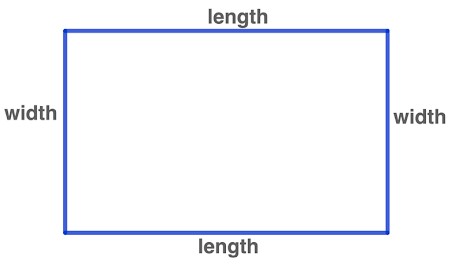
Shapes have properties that enable us to recognize them as such. Different shapes form depending on the number of sides and corners a shape has. The side of a two-dimensional (2D) object is a straight line, and the corner is where the two sides meet. A vertex is another word for a corner; as a result, an angle is created. The shape below shows that it has four sides, four corners, and four angles.

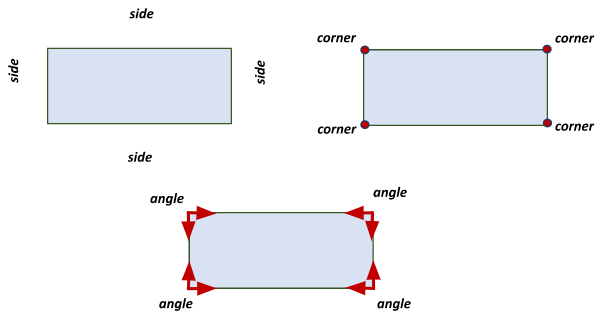
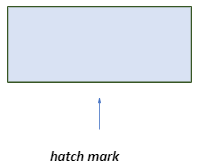
The equal length of a shape’s sides serves as a description. Equal-length sides are denoted with a hatch mark (“|”). The figure below shows how the opposite sides are equal in length. The measurement of the sides with a single hatch mark and the sides with two marks are different.

When describing shapes, keeping parallel lines in mind can be useful. Parallel lines are those whose distances between them are consistent. As the broken red lines in the illustration below shows, the parallel lines do not move in any direction toward or away from one another.

The common 2D shapes are shown below along with their attributes.

Circle

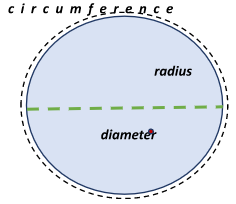
A circle is a curved, non-cornered shape in two dimensions. Its characteristics include radius, diameter, circumference, and other measurements. 

• There are no sides or edges in a circle. It’s round.
• The circumference of a circle is the distance that runs around it.
• The radius is the distance from a circle’s center to a location on the circle.
• The diameter is the line segment that has endpoints on the circle and passes through its center.

These are examples of circles in real life.

Polygons

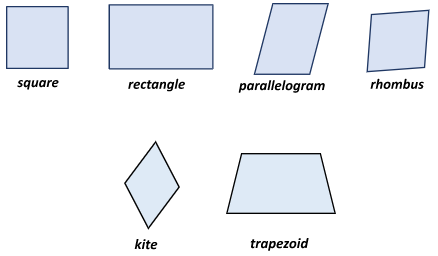
Two-dimensional objects called polygons are those with a definite number of sides. Polygons have sides that are end-to-end connections of straight-line segments. Examples of regular polygons with equal sides and angles are triangle, parallelogram, square, rectangle, rhombus, kite, and trapezoid.

There are several types of polygons that have distinct names based on characteristics that define them, such as the number of sides, edges, corners, and angles.

Triangle

Triangles are polygons with three sides. Based on the lengths of their sides, triangles can be categorized as scalene, isosceles, and equilateral. Based on their angles, triangles might be acute, obtuse, or right.

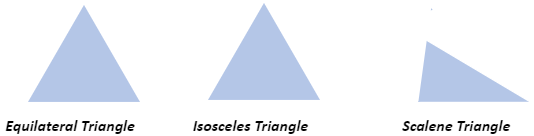
The isosceles triangle has two equal sides, the scalene triangle has varied sizes, and an equilateral triangle has three equal sides. 

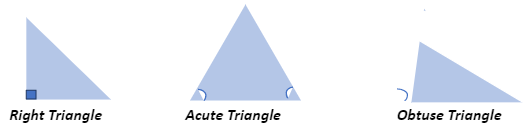
A triangle has internal angles that sum to 180 degrees. Angles in acute triangles are all under 90 degrees. A right triangle has one side that is 90 degrees in angle. A triangle is said to be obtuse if one angle is more than 90 degrees.

Quadrilaterals

The words “quad” ( four ) and “lateral” ( side ) are the origins of the term quadrilateral. Four sides, four vertices, and four angles make up the family of shapes known as quadrilaterals. There are subtle variations in every quadrilateral shape that distinguish them from one another. The various kinds of quadrilaterals and their attributes are listed below:

Parallelogram

Parallel lines create a parallelogram’s four sides and four corners. A parallelogram’s opposite sides are parallel, but the angles may not be the same. Square, rectangle, and rhombus are the three diverse types of parallelograms.

The red line segments stand for the parallel opposite sides of the rectangles.

Square

Four sides and four corners make up a square. The square has equal-length sides. Two parallel sets of sides make up a square.

The corners of the square are represented by the red dots.
The hatch marks show the equal length of the sides.

Rectangle

Four sides and four corners make up a rectangle. In a rectangle, the length of the two opposite side pairs is equal. A rectangle’s two sets of sides are parallel.

The corners of the rectangle are shown by red dots.
The rectangle’s opposite sides are equal in length, as shown by the hatch marks.

Rhombus

Rhombuses can also be referred to as diamonds. A rhombus has four sides and four corners. A rhombus resembles a square tilted to the side. The sides are the same length. A rhombus has parallel opposing sides.

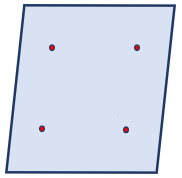
The hatch marks show that the sides of the rhombus are equal in length.
The corners of the rhombus are represented by the red dots.

Kite

A kite has four sides and four corners. A kite has two sets of sides that are the same length.

Parallel sides are never possible for a kite.

The hatch marks show that the sides of the rhombus are equal in length.

Trapezoid

There is only one set of parallel sides in a trapezoid. (They say “trapezium” in India and Britain)

The parallel opposite sides are shown in red line segments.

There are further unique varieties of trapezoids, including isosceles, acute, obtuse, and right trapezoids. They are distinct from one another due to their varying side lengths and interior angles. 

The family of quadrilaterals includes parallelogram, square, rectangle, rhombus, kite, and trapezoid. This diagram shows the relationship of the different quadrilaterals based on their properties.

Venn Diagram ( Classification of Quadrilaterals)

Rectangle, square, and rhombus have the characteristics of a parallelogram. These three shapes are all parallelograms as a result. Rectangle and rhombus both have the characteristics of a square, therefore we say that a square is both a rectangle and a rhombus.

Polygons with more than four sides

The following are examples of polygons with more than four sides. 

Five equal-length sides make up the pentagon. It has a total of 540 degrees in interior angles. A regular pentagon has 108 degrees in each of its angles.

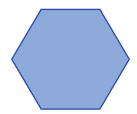
 A hexagon is a polygon with six sides. Its inner angles equal 720 degrees in total. In a regular hexagon, each angle is 120 degrees. 

Heptagon refers to a polygon with seven sides. The sum of its inner angles is 900 degrees. A regular heptagon has 128.57 degrees angles on each vertex.

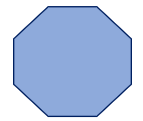
An octagon is an eight-sided polygon. Its total interior angles are 1080 degrees. Each angle measures 135 degrees in a regular octagon.

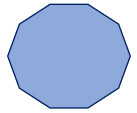
The term “decagon” refers to a polygon with ten sides. The total of its interior angles is 1440 degrees. A regular decagon has 144 degrees for each angle.

Describing 3D Shapes

Shapes with three dimensions (3D) occupy space. They have length, width, and height. They are all the items we can hold like a pencil, cellphone, table, etcetera. 

All three-dimensional shapes have characteristics. Faces, edges, and corners are a few of these attributes.

• A three-dimensional shape’s face is a flat surface. Often, the faces are 2D shapes.
• The boundary between two of its surfaces is known as the edge.
• A corner is created when two or more edges meet. Like 2D shapes, a corner is also referred to as a vertex.

The following are the common 3D shapes along with descriptions of each. 

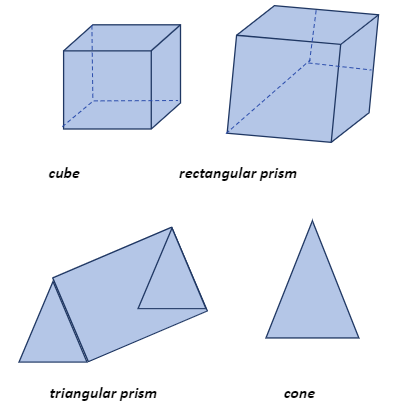
Cube

There are six identical faces on a cube. A cube has squares on each of its faces. There are 12 edges on it with eight corners. The faces, edges, and corners are all the same size and length.

Rectangular Prism

There are six faces on a rectangular prism. A rectangle makes each face. The size of the opposite faces is constant. It has 12 edges and eight corners.

Triangular Prism

A triangular prism has five faces. It features three rectangle-shaped faces and two triangle-shaped faces. The sizes of the two triangular faces are the same. . It has 6 corners and 9 edges.

Cylinder

A cylinder has a tube in the middle and two circles of the same size on each end. It features one curved surface and two flat faces. A cylinder has two edges and no corners.

Cone

At the base of a cone is a circle, and at the other end is a point. There is one flat face and one curved surface. A cylinder has a single edge without any corners.

Sphere

A spherical has the ideal roundness. The surface of it is curved. A sphere does not have flat faces, edges, or corners. On the sphere, the distance between each point and the center is constant.

Real-Life Examples of 3D Shapes

These illustrations are examples of 3D objects that surround us.

Practice with Shapes

Question 1: How many corners does a triangular prism have?

Answer:  Six corners

Question 2: True or False: A square has three sides and three corners. 

Answer:  False

Question 3: Which property of the given shape is shown by the arrows below?

Answer:  Corners or vertices

Question 4: Which of the following is not an attribute of this shape?

Choices: 

Four vertices

Four sides

Two pairs of parallel sides

Answer:  Two pairs of parallel sides

Question 5: Which polygon has 5 sides?

Answer:  Pentagon

Question 6: How many corners or vertices does a circle have?

Answer:  zero ( 0 )

Question 7: Identify the defining and non-defining attributes of the shape below?

4 sides red 4 corners checkered       closed       big

2 pairs of parallel sides with opposite sides have equal lengths

Answer:  Defining attributes: 4 sides, 4 corners, closed  2 pairs of parallel sides, 

   opposite sides have equal lengths

      Non–defining attributes: red, checkered, big

Question 8: Which triangle has no equal sides?

Isosceles Triangle

Scalene Triangle

Equilateral Triangle

Answer:  Scalene Triangle

Question 9: Which of the following are quadrilaterals?

Square Hexagon Rectangle Parallelogram

Rhombus Circle Triangle Trapezoid

Kite Octagon Decagon Heptagon

Answer:  Square, Rectangle, Parallelogram, Rhombus, Trapezoid, Kite

Question 10: What three-dimensional shape is illustrated in the picture below?

Answer:  Sphere

Question 11: Find the number of faces and vertices that this shape has.

Answer:  A cube has 6 faces and 8 vertices.

Question 12: Which of the following statements is false?

All squares have 4 equal sides.

All rectangles have 4 vertices.

A rhombus is a square.

A square is a rectangle.

Answer:  A rhombus is a square. 

To make the statement correct, it should be changed to:

 A square is a rhombus.

Question 13: Which of the following is a closed two-dimensional shape with straight sides?

Circle Polygon Prism Cone

Answer:  Polygon

Question 14: Which shape is illustrated below?

Answer:  Hexagon

Question 15: What attributes below describe this shape?

Choices:  curved surface, 0 vertices 2 faces

    3 faces 1 vertex triangular base

Answer:  curved surface, 0 vertices, 2 faces

Question 16: A flat surface of a shape is called ________.

Answer:  a face

Question 17: Which shape has 8 vertices?

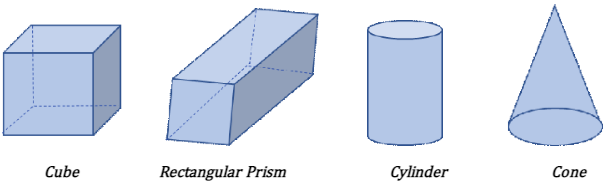
Answer:  Rectangular Prism

Question 18: The figure shown is made from two three-dimensional shapes. One of the shapes is a sphere, what is the other shape?

Answer:  a cube

Question 19: Select all defining attributes of a rectangular prism.

      Choices:  

6 faces 8 faces 12 faces

6 edges 8 edges 12 edges

6 corners 8 corners 12 corners

A rectangle makes each face.

A triangle makes each face.

Answer:  A rectangle makes each face.

    6 faces, 12 edges, and 8 corners

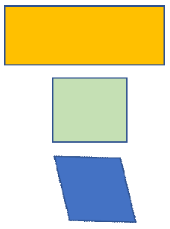
Question 20: Complete the statement below

The shapes are all _____________________. 

Choices:

Cubes 

Parallelograms

Trapezoids

Triangles

Answer:  The shapes are all parallelograms. 

Parallelograms include squares, rhombuses, and rectangles. 

These shapes all have the characteristics of parallelograms.

Question 21: Select all defining attributes of a triangular prism.

      Choices:  

4 faces 5 faces 6 faces

8 edges 9 edges 10 edges

6 corners 7 corners 8 corners

Answer:  5 faces, 9 edges, and 6 corners

Question 22: Which of the following are three-dimensional shapes?

Square Cube Rectangular Prism Parallelogram

Rhombus Cone Triangular Prism Trapezoid

Cylinder Octagon Decagon Sphere

Vertex Angle Sides Vertex

Answer:  Cube, Rectangular Prism, Triangular Prism, Cylinder, Sphere, Cone

Question 23: Identify the polygons with more than 4 sides.

Square Hexagon Rectangle Parallelogram

Rhombus Circle Triangle Trapezoid

Kite Octagon Decagon Heptagon

Pentagon Cube Cone Cylinder

Sphere Angle Corner Vertex

Answer:  Pentagon, Hexagon, Heptagon, Octagon, Decagon

Question 24: Match the polygons to their corresponding number of sides.

Polygons Number of Sides

Decagon         6 sides

Triangle         4 sides

Heptagon         7 sides

Octagon         3 sides

Quadrilateral       10 sides

Pentagon         8 sides

Hexagon               5 sides

Answer:  Decagon – 10 sides, Triangle – 3 sides, Heptagon – 7 sides, Octagon – 8 sides, 

  Quadrilateral – 4 sides, Pentagon – 5 sides, Hexagon – 6 sides

Question 25: 

True or False: If the statement is true, write True; if not, write False.

1. There are four sides to every trapezoid.
2. Every parallelogram is a rhombus.
3. Rectangles are parallelograms.
4. Flat shapes are three-dimensional.
5. A cone is a two-dimensional shape.
6. There are six faces on cubes and rectangular prisms.
7. Edges are another word for a shape’s sides.
8. A triangle is a quadrilateral.
9. A cone has a circular base.
10. A kite has parallel sides.

Answer:  

1. True.
2. False. In contrast to a rhombus, a parallelogram does not have equal sides.
3. True.
4. False. Flat shapes are two-dimensional.
5. False. A cone is a three-dimensional shape.
6. True.
7. True.
8. False. Quadrilaterals have four sides and corners, while triangles only have three.
9. True.
10. False. A kite does not have parallel sides.

Summary

• The characteristics of a shape or a specific object are referred to as its “attributes”.
• There are defining and non-defining attributes when analyzing shapes. Defining attributes are distinguishing characteristics of shapes while non-defining attributes do not always apply to the shapes. 
• Defining attributes of shapes include sides, corners, or vertices, and these shapes must be closed figures. There are some shapes have distinctive attributes that set them apart from other shapes.
• non-defining attributes include colors, sizes, orientation, and patterns.
• The sides of shapes with equal length are denoted with hatch marks (“|”).
• The comparison of two-dimensional and three-dimensional shapes is presented below.

Two-dimensional ( 2D) Shapes

• Shapes that are two-dimensional (2D) are flat shapes.
• Shapes that are two-dimensional (2D) are flat shapes.
• Circles and polygons are examples of 2D shapes. The following are examples of polygons: triangles, pentagons, hexagons, heptagons, octagons, and decagons, as well as quadrilaterals (square, rectangle, rhombus, parallelogram, trapezoid, and kite).

Three–dimensional ( 3D ) Shapes

• Shapes with three dimensions (3D) occupy space. 
• Length, width, and height are attributes of 3D shapes.
• Cube, rectangular prism, triangular prism, cylinder, cone, and sphere are some examples of 3D shapes.
• The attributes of the common two-dimensional (2D ) shapes are displayed in the table below. All except the circle are polygons. Quadrilaterals are shapes like parallelogram, square, rectangle, rhombus, kite, and trapezoid.

Common two-dimensional shapes and their attributes

Shape	Edges	Corners	Parallel Sides
Circle	Zero ( 0 )	Zero ( 0 )	Zero ( 0 )
Triangle	Three ( 3 )	Three ( 3 )	None
Parallelogram	Four ( 4 )	Four ( 4 )	Two pairs
Square	Four (4 )	Four ( 4 )	Two pairs
Rectangle	Four (4 )	Four ( 4 )	Two pairs
Rhombus	Four (4 )	Four ( 4 )	Two pairs
Kite	Four (4 )	Four ( 4 )	Zero ( 0 )
Trapezoid	Four (4 )	Four ( 4 )	One pair

• There are polygons with more than four sides as well. The pentagon (five sides), hexagon (six sides), heptagon (7 sides), octagon (eight sides), and decagon are a few examples of these polygons ( 10 sides ).
• The attributes of the common three-dimensional ( 3D )  shapes are displayed in the table below.

Common three-dimensional shapes and their attributes

Shape	Edges	Faces	Vertices
Cube	Twelve ( 12 )	Six ( 6 )	Eight ( 8 )
Rectangular Prism	Twelve ( 12 )	Six ( 6 )	Eight ( 8 )
Triangular Prism	Nine ( 9 )	Five ( 5 )	Six ( 6 )
Cylinder	Two ( 2 )	Two (2 ) ( One  curved surface )	Zero ( 0 )
Cone	One ( 1 )	One ( 1 )( One curved surface )	One ( 1 )
Sphere	Zero ( 0 )	One curved surface	Zero ( 0 )

• Mathematics requires an understanding of shapes. Although understanding their features has practical implications and is useful in everyday settings, this is something that we must learn in school. Engineers, architects, artists, estate agents, farmers, and construction workers are just a few of the professions that need to understand the attributes of shapes.
• As shapes are all around us, it is important to learn their characteristics. Activities involving classification and sorting contribute to the development of a variety of thinking skills as well as supply the foundations for future problem-solving.

Recommended Worksheets

Basic Shapes (International Day of PWD’s Themed) Math Worksheets
Spatial Skill: Circles (New Year’s Eve Themed) Math Worksheets
Kinds of Shapes (Christmas Themed) Math Worksheets