Introduction
Many examples of basic plane Euclidean geometry make use of the inscribed angle. Other theorems relating to the power of a point with respect to a circle are based on the inscribed angle. The inscribed angle plays an important role in the circle theorems. The inscribed angle is the foundation for several circle theorems.
In this article, we will define inscribed angles and other associated concepts, measure inscribed angles, and learn inscribed angles conjectures using examples that have been solved.
What is an inscribed angle?
Definition
An angle is said to be inscribed if its vertex is on the circumference of the circle and both of its sides are chords of the same circle. The arc created by the inscribed angle is the intercepted arc. The intercepted arc is the arc that lies in the interior of an inscribed angle and has endpoints on the angle.
In the circles below, we have circles P, S and G.
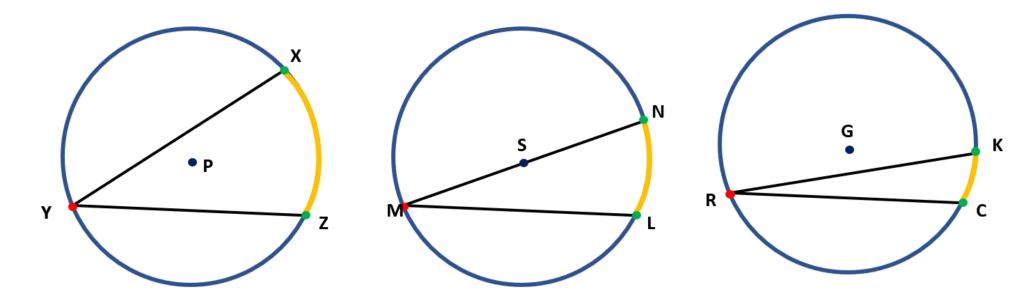
In circle P, the inscribed angle is ∠ XYZ. Notice that the vertex Y is on the circumference of the circle while the sides of the angle are the chords $\overline{YX}$ and $\overline{YZ}$. The intercepted arc formed is arc XZ ( XZ). The center is in the interior of the inscribed angle.
In circle S, the intercepted arc is ∠ LMN. The intercepted formed is arc LN. The sides of the intercepted arc are the chords $\overline{MN}$ and $\overline{ML}$. The chord $\overline{MN}$ is also the circle’s diameter since it passes through the center of circle S.
In circle G, the intercepted arc of the inscribed angle ∠ KRC is arc KC. The circle’s center is outside of the inscribed angle or exterior of the inscribed angle.
Identifying and Measuring Inscribed Angles
By examining two chords that share an endpoint, it is necessary to identify the inscribed angle of the circle. The vertex of the inscribed angle is where the two chords’ common endpoints meet. We use three letters to name the inscribed angle, with the vertex being the middle letter and the other endpoints being the other two letters.
For example, we have circle M below. We have the chords $\overline{AR}$ and $\overline{AE}$. The common endpoint or the vertex is point A. Therefore, the inscribed angle of the circle is ∠ EAR or ∠ RAE.
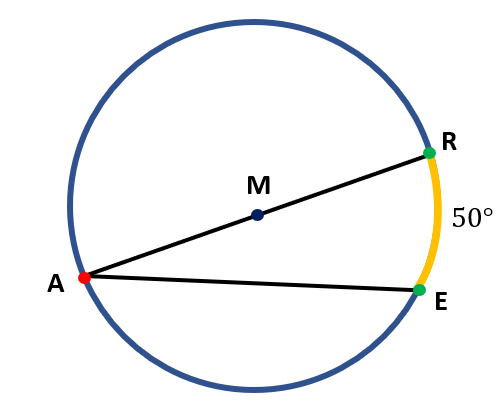
Get ½ of the intercepted arc’s measure in order to determine the measure of the inscribed angle formed by the two chords. Simply expressed, we can multiply by ½ or divide by 2 the measurement of the intercepted arc to get the measurement of the inscribed angle.
Inscribed Angle Theorem
The measurement of an angle equals one-half the size of its intercepted arc if the angle is inscribed in a circle.
So, in the given circle M, since the measure of the intercepted arc RE is 50°, the measure of the inscribed angle ∠ RAE is 25°.
m ∠ RAE= ½ ( m RE )
m ∠ RAE= ½( 50° )
m ∠ RAE= $\frac{50^o}{2}$
m ∠ RAE= 25°
Conjectures About Inscribed Angles
Inscribed Angle Conjecture
An inscribed angle in a circle has a measure that is half that of the central angle with the same intercepted arc.
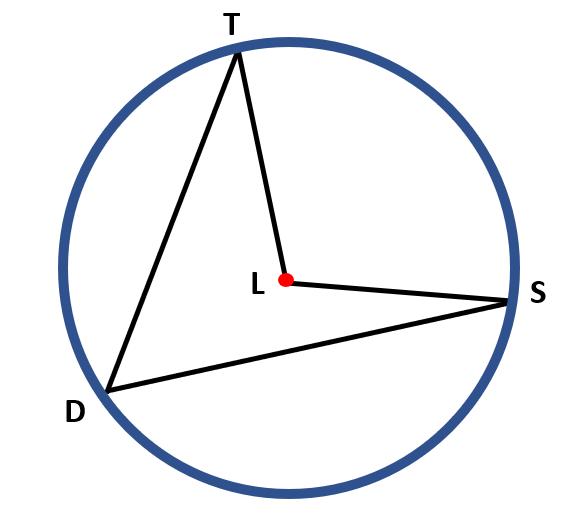
m ∠ TDS=½( m ∠ TLS )
In the figure, ∠ TDS is an inscribed angle, while ∠ TLS is a central angle. Both angles intersect the same arc, which is TS.
Let us say, for example, the measure of ∠ TLS is 220°, then the measure of ∠ TDS is 110°.
m ∠ TDS= ½( m ∠ TLS )
m ∠ TDS= ½( 220° )
m ∠ TDS= $\frac{220^o}{2}$
m ∠ TDS= 110°
Inscribed Angles Intercepting Arcs Conjecture
Two inscribed angles in a circle that share the same intercepted arc are congruent.
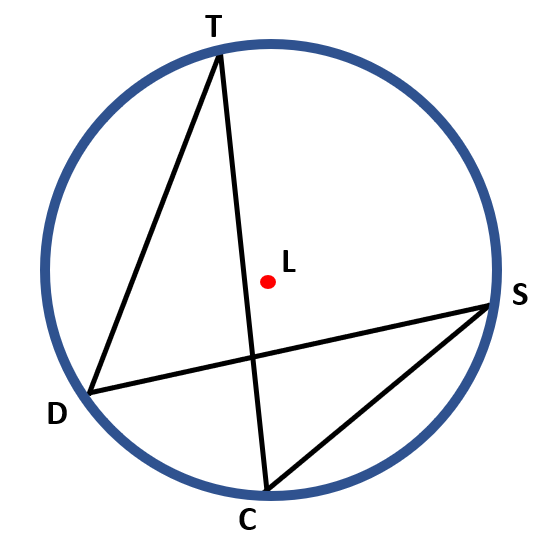
m ∠TDS≅m ∠ TCS
∠ TDS and ∠TCS are inscribed angles and share the same intercepted arc TS.
Let us say, for instance, the measure of ∠ TDS is 50°, then the measure of ∠ TCS is also 50°.
Inscribed Angles in a Semi-circle Conjecture
Any angle that is inscribed in a semi-circle is a right angle.
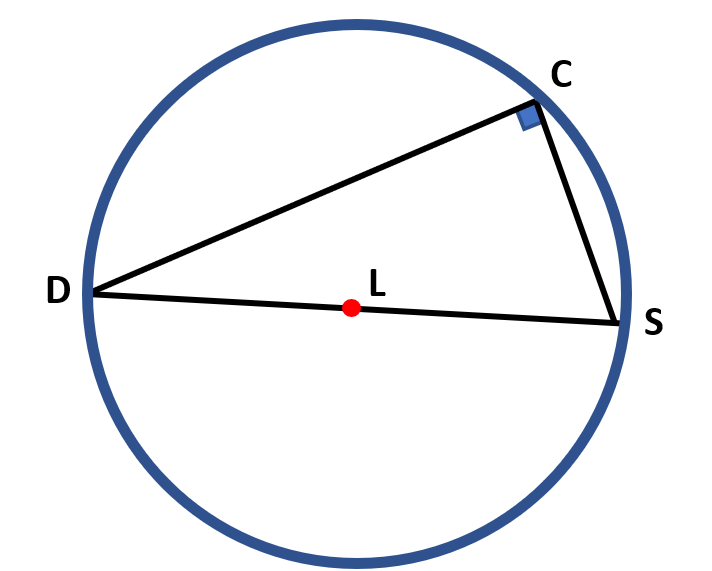
m ∠ DCS=90°
In the figure, ∠DCS is an inscribed angle, and $\overline{DS}$ is a diameter of the circle L
More Examples
Example 1
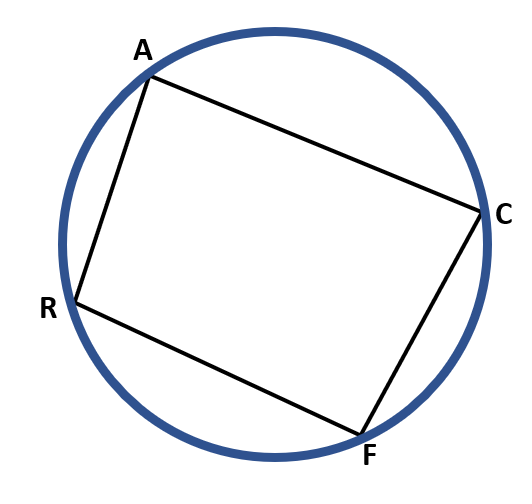
Identify the inscribed angles and their intercepted arc in the given circle below.
Solution:
The circle has four inscribed angles:
∠ RAC or ∠ CAR with intercepted arc CR or RC,
∠ ACF or ∠ FCA with intercepted arc AF or FA,
∠ CFR or ∠ RFC with intercepted arc CR or RC, and
∠ ARF or ∠ FRA with intercepted arc AF or FA.
Example 2
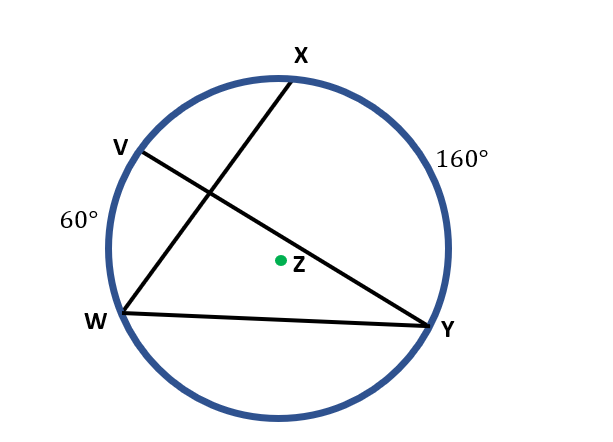
Find the measure of the inscribed angles ∠ XWY and ∠ VYW.
Solution:
The intercepted arc of ∠ XWY is the XY which measures 160°. To find the measure of ∠ XWY, we get ½ of 160°. Here is the math,
m ∠ XWY= ½ ( m XY )
m ∠ XWY = ½( 160° )
m ∠ XWY= $\frac{160^o}{2}$
m ∠ XWY= 80°
The inscribed angle ∠ VYW has an intercepted arc VW which measures 60°. To get the measure of ∠ VYW, we get half of 60°. That is,
m ∠ VYW=½ ( m VW )
m ∠ VYW=½( 60° )
m ∠ VYW=$\frac{60^o}{2}$
m ∠ VYW=30°
Thus, the measures of the inscribed angles ∠XWY and ∠VYW are 80° and 30°, respectively.
Example 3
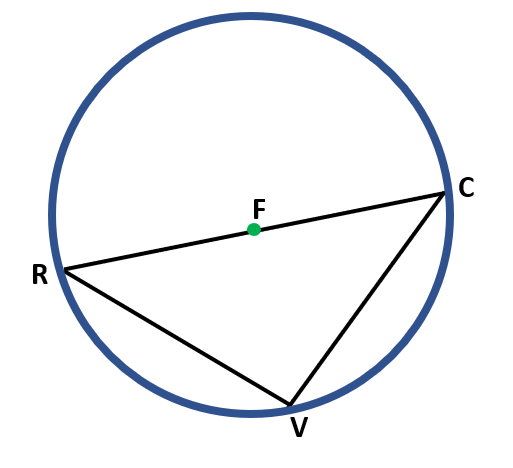
Find m ∠ RVC in circle F.
Solution:
∠ RVC is an intercepted arc. We can get its measurement by first identifying the measurement of its intercepted arc RC.
It can be observed that the chord $\overline{RC}$ is a diameter since it passes through the center of circle F. ∠ RFC forms a straight angle which measures 180°. Since ∠ RFC is a central angle, an angle whose vertex is the center of the circle, then the measure of RC is also 180°.
To get the measure of the inscribed angle ∠RVC, we must divide 180° by 2. We have,
m ∠ RVC=½ m RC
m ∠ RVC=½( 180° )
m ∠ RVC=$\frac{180^o}{2}$
m ∠ RVC=90°
Therefore, the measure of the ∠ RVC is 90°.
Example 4
Complete the table below.
| Inscribed Angle | Intercepted Arc |
| m ∠ BTS= 80° | m BS= ? |
| m ∠ DLS= ? | m DS=78° |
| m ∠ LOR= 55° | m LR= ? |
| m ∠ MID= ? | m MD=12.5° |
Solution:
If the inscribed angle’s measurement is what is missing, we must multiply the intercepted arc’s given measurement by ½ . On the other hand, if the intercepted arc’s measurement is missing, we must multiply the given measurement of the inscribed angle by 2.
To find m BS, given that m ∠ BTS=80°,
m BS= 2 (m ∠ BTS )
m BS= 2( 80° )
m BS= 160°
To find m ∠DLS, given that m DS}=78°,
m ∠DLS= ½ m BS
m∠ DLS= ½ 78°
m ∠ DLS= $\frac{78^o}{2}$
m ∠ DLS= 39°
To find m LR, given that m ∠LOR=55°,
m BS= 2( m ∠LOR )
m LR= 2( 55° )
m LR= 110°
To find m ∠MID, given that m MD=12.5°,
m ∠ MID=½ ( m MD )
m ∠ MID= ½( 12.5° )
m ∠ MID= $\frac{12.5^o}{2}$
m ∠ MID= 6.25°
Therefore, here is the completed table.
| Inscribed Angle | Intercepted Arc |
| m ∠ BTS=80° | m BS= 160° |
| m ∠ DLS=39° | m DS=78° |
| m ∠ LOR=55° | m LR= 110° |
| m ∠ MID=6.25° | m MD=12.5° |
Example 5
Find the measure of ∠ CVG and m CG.
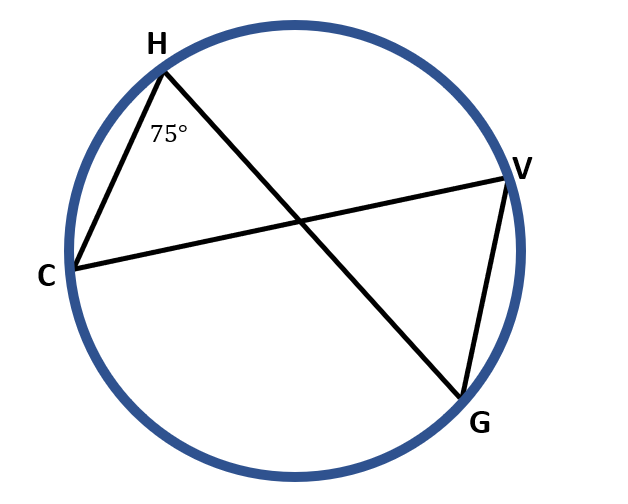
Solution:
Any two inscribed angles in a circle that share the same intercepted arcs are congruent. In this example, the inscribed angles ∠ CHG and ∠ CVG have the same intercepted arc CG. Thus, we may say that ∠ CHG is congruent with ∠ CVG or ∠ CHG≅∠ CVG.
Since m ∠ CHG=75°, then ∠ CVG measures 75° too.
To find the measure of CG, we must multiply the measure of ∠ CHG by 2. So, we have,
m CG=2( m ∠CHG )
m CG=2( 75° )
m CG=150°
Therefore, the m ∠ CVG=75° and m CG=150°.
Example 6
In each case, find the value of x.
a )
b )
c )
d )
Solution:
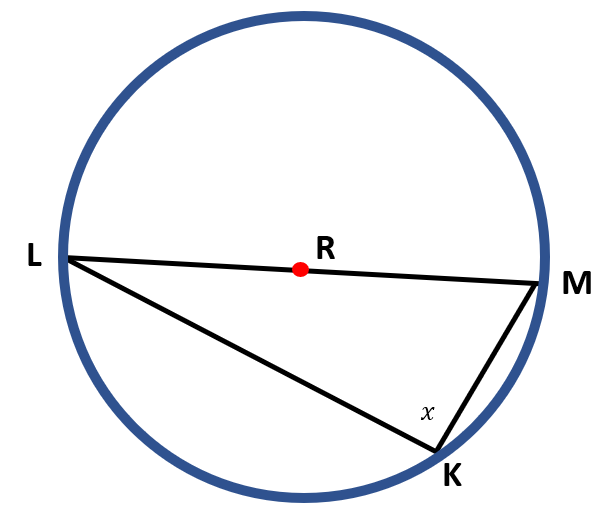
a ) The inscribed angle in circle R that we need to find the value of x is ∠ LKM. Notice that the chord $\overline{LM}$ is a diameter of circle R, which divides the circle into two semi-circles. Thus, the measure of arc LM is 180°.
∠ LKM measures 90° because the measure of an inscribed angle is half the measure of its intercepted arc, then
m ∠LKM= ½( m LM )
m ∠ LKM= ½( 180° )
m ∠ LKM= $\frac{180^o}{2}$
m ∠ LKM= 90°
Thus, x= 90°.
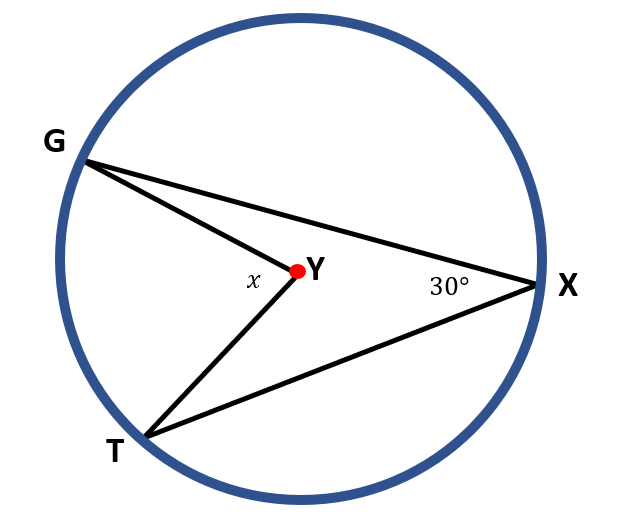
b ) In circle Y, ∠ GXT is an inscribed angle, while ∠ GYT is a central angle. Since both angles share the same arc, which is GT, then the measure of ∠ GYT is twice the measure of ∠ GXT. That is,
m ∠ GYT=2( m ∠ GXT )
m ∠ GYT=2( 30° )
m ∠ GYT=60°
Therefore, the value of x is 60°.
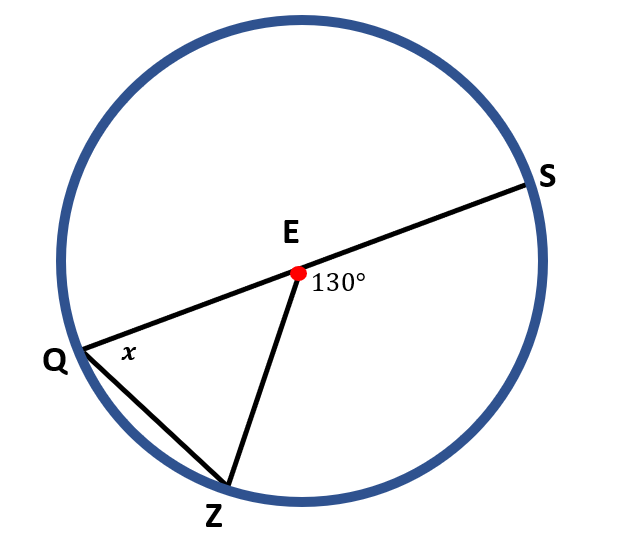
c ) ∠ ZES is a central angle that measures 130°, and we are asked to find the measure of the inscribed angle ∠ ZQS. Since both ∠ ZES and ∠ ZQS share the same intercepted arc, then m ∠ ZQS is half the m ∠ ZES.
m ∠ ZQS= ½ m( ∠ ZES)
m ∠ ZQS= ½( 130° )
m ∠ ZQS= $\frac{130^o}{2}$
m ∠ ZQS= 65°
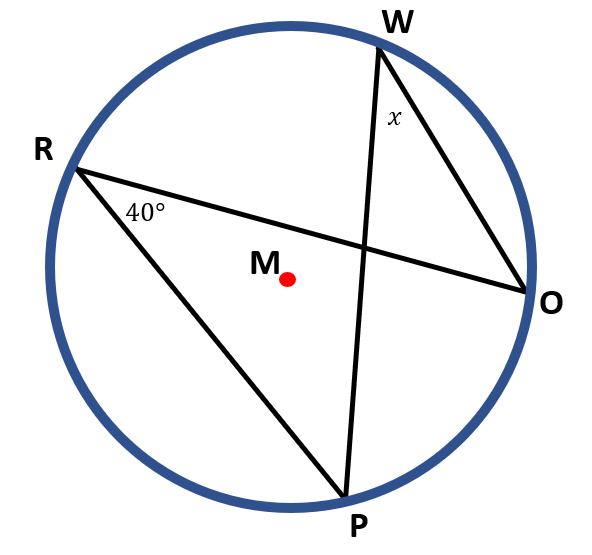
d ) In circle M, both ∠ PRO and ∠ PWO are inscribed angles that share the same intercepted arc PO. Thus, m ∠ PRO≅m ∠ PWO.
Since it is given that m ∠PRO=40°, then the m ∠ PWO is also 40°.
Example 7
Solve for the value of x.
Solution:
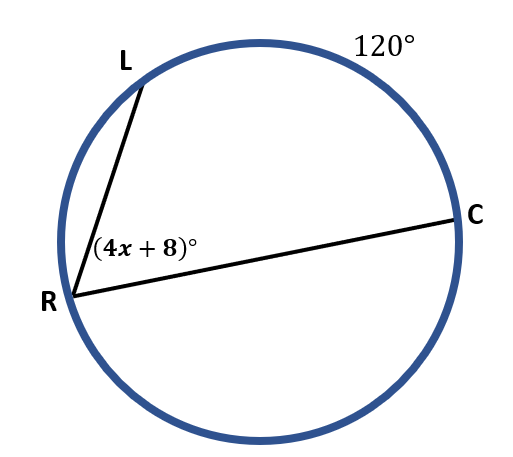
In the given illustration, we have m LC=120° and m ∠ LRC=(4x+8)°. Since ∠LRC is an inscribed angle, its measure is ½ of the measure of its intercepted arc LC.
m ∠LRC= ½( m LC )
m ∠ LRC= ½( 120° )
m ∠ LRC= $\frac{120^o}{2}$
m ∠ LRC= 60°
Since we already know that the measure of the inscribed angle is 60°, we may now solve for the value of x, that is,
$4x + 8 = 60$
$4x = 60-8$
$4x = 52$
$\frac{4x}{4} = \frac{52}{4}$
$x= \frac{52}{4}$
$x=13$
Therefore, the value of x is 13.
To check, we may substitute 13 to the given expression, and it should equate to 60.
4(13)+8= 60
52+8= 60
60= 60
Example 8
Find the value of x given that the measure is arc AB is 100°.
Solution:
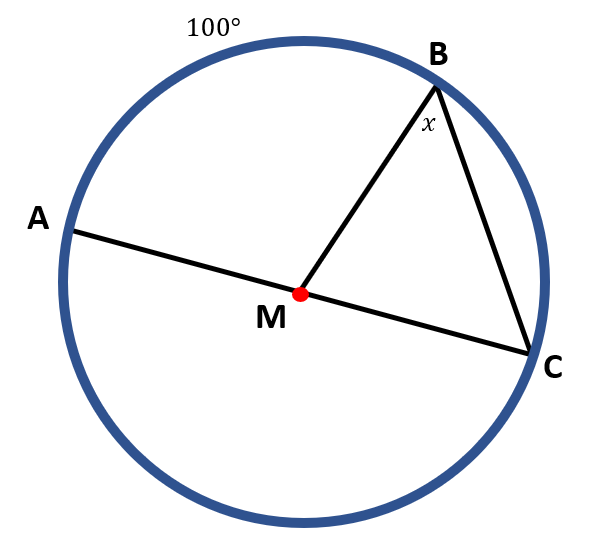
In circle M, ∠ ACB is an inscribed angle with intercept arc AB. Since m AB=100°, the measure of ∠ ACB is half of m AB, which is 50°. We have,
m ∠ACB= ½( m AB )
m ∠ ACB= ½( 100° )
m ∠ ACB= $\frac{100^o}{2}$
m ∠ ACB= 50°
Notice that AC is an arc of a semi-circle; therefore, since m AB=100°, the measure of BC is 80°.
m BC=180°-m AB
m BC=180°-100°
m BC=80°
Since ∠ BMC is a central angle with the intercepted arc BC, its measure is also 80°.
Notice that angles ∠ B, ∠ C, and ∠ M form a triangle. Remember that the sum of the angles in a triangle is equal to 180°. Thus, we can find the value of x, the m ∠ B, by subtracting the sum of angles ∠ C and ∠ M from 180°. Hence,
m ∠ B=180°- ( m ∠ C+m ∠ M )
m ∠ B=180°- ( 50°+ 80° )
m ∠ B=180°-130°
m ∠ B=50°
Therefore, the value of x is 50°.
Example 9
Solve for x.

Solution:
In the given circle with center P, ∠ VFD is an inscribed angle that measure 105°. To get the measure of the central angle ∠ DPV, we must multiply the m ∠ VFD by 2. Remember that the measure of a central angle is twice the measure of the inscribed angle if they share the same intercepted arc. Hence,
m ∠ DPV=2 ( m ∠ VFD )
m ∠ DPV=2( 105 )
m ∠ DPV=210°
Let us now equate ( 3x+6 )° to 210° to find the value of x. We have,
$3x+6=210$
$3x=210-6$
$3x=204$
$\frac{3x}{3}=\frac{204}{3}$
$x=68$
Therefore, the value of x is 68°.
Example 10
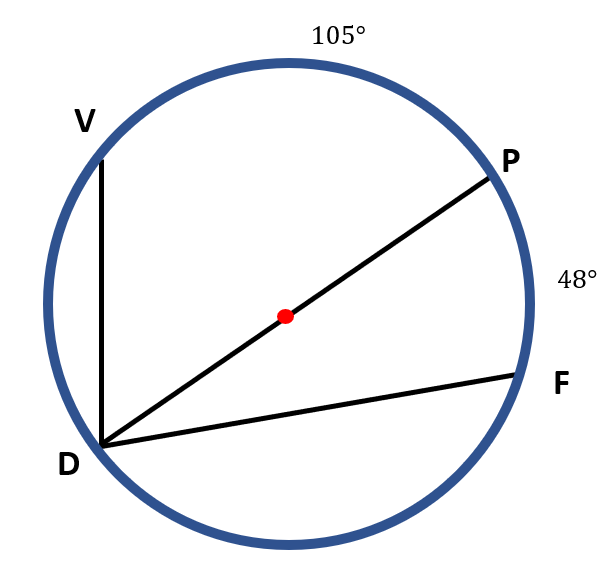
In the figure below, points D, V, P, and F are on the circle. Find the measure of ∠ VDF if m VP=105° and m PF=48°.
Solution:
∠ VDF is an inscribed angle since the points VDF are on the circumference of the circle. Adding the m VP and m PF gives the m VF which is the intercepted arc of the angle ∠ VDF. To find the measure of ∠ VDF, we must get half the sum of the measures of VP and PF. Thus,
m ∠ VDF=½( m VP+m PF )
m ∠ VDF=½( 105°+48° )
m ∠ VDF=½( 153° )
m ∠ VDF=$\frac{153^o}{2}$
m∠ VDF=76.5°
Summary
An angle is said to be inscribed if its vertex is on the circumference of the circle and both of its sides are chords of the same circle.
The intercepted arc is the arc that lies in the interior of an inscribed angle and has endpoints on the angle.
Inscribed Angle Theorem
The measurement of an angle equals one-half the size of its intercepted arc if the angle is inscribed in a circle.
The term “central angle” refers to an angle whose vertex is at the center of the circle. Its measure is equal to its intercepted arc.
A chord that passes the circle’s center is referred to as the diameter.
Identifying Inscribed Angles
By examining two chords that share an endpoint, it is necessary to identify the inscribed angle of the circle. The vertex of the inscribed angle is where the two chords’ common endpoints meet. We use three letters to name the inscribed angle, with the vertex being the middle letter and the other endpoints being the other two letters.
Measuring Inscribed Angles Given its Intercepted Arc
Get 1/2 of the intercepted arc’s measure in order to determine the measure of the inscribed angle formed by the two chords. Simply expressed, we can multiply by 1/2 or divide by 2 the measurement of the intercepted arc to get the measurement of the inscribed angle.
Conjectures About Inscribed Angles
Inscribed Angle Conjecture
An inscribed angle in a circle has a measure that is half that of the central angle with the same intercepted arc.
Inscribed Angles Intercepting Arcs Conjecture
Two inscribed angles in a circle that share the same intercepted arc are congruent.
Inscribed Angles in a Semi-circle Conjecture
Any angle that is inscribed in a semi-circle is a right angle.
Frequently Asked Questions (FAQs)
What is meant by inscribed angle?
An angle is said to be inscribed if its vertex is on the circumference of the circle and both of its sides are chords of the same circle.
What is the difference between a central angle and an inscribed angle?
An angle is said to be inscribed if its vertex is on a circle and both of its sides are chords of that circle.
A central angle, on the other hand, has a vertex at the center of the circle and two radii as its sides.
For example, we have the image below with circle P and its central and inscribed angles.
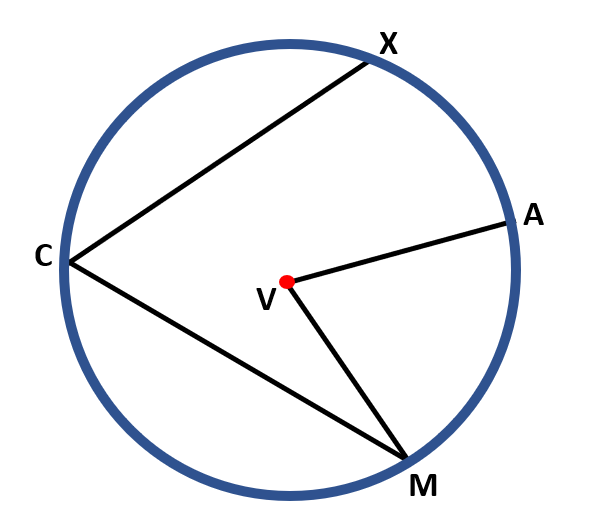
The central angle in circle V is ∠ AVM or ∠ MVA. The vertex of ∠ AVM is the center of the circle, and the two radii $\overline{VM}$ and $\overline{VA}$ are the sides.
The inscribed angle in circle V is ∠ XCM or ∠ MCX. The vertex of ∠ XCM lies on the circle, and the two chords $\overline{CX}$ and $\overline{CM}$ are the sides.
How are inscribed and central angles related to one another?
The measure of a central angle would be double the inscribed angle if a central angle and an inscribed angle both intersect the same arc. To put it simply, the measure of an inscribed angle is half of the measure of the central angle.
For example, the figure below shows circle V with the measure of arc PR equals 80°. Both the central angle( ∠PVR )and the inscribed angle (∠PQR ) intersect the same arc PR, then the measure of ∠ PVR is twice the measure of ∠ PQR
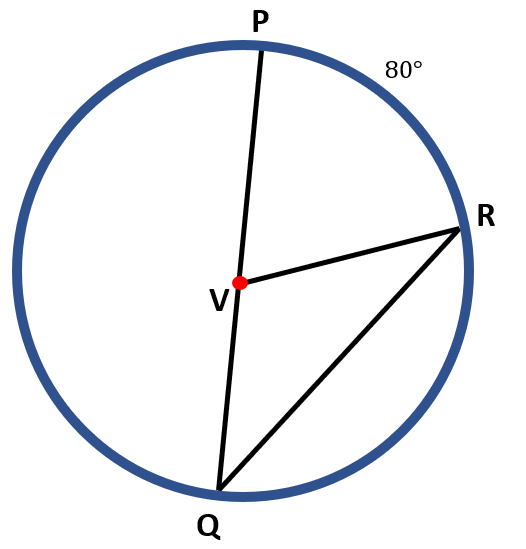
The measure of the central angle ∠ PVR=80° is the measure of its intercepted arc PR. For the measure or ∠ PQR, we have,
m ∠ PQR=½ m PR
m ∠ PQR=½( 80° )
m ∠ PQR=$\frac{80^o}{2}$
m ∠ PQR=40°
Therefore, m ∠ VPR=80° while m ∠ PQR=40°.
How can I find the measure of an inscribed angle?
To find the measure of an inscribed angle, get ½ of the intercepted arc’s measure formed by the two chords. Simply expressed, we can multiply by ½ or divide by 2 the measurement of the intercepted arc to get the measurement of the inscribed angle.
Let us say, for example, that the measure of the intercepted arc in the given image below is 210° or m AF=210°. To find the measure of the inscribed angle, which is ∠ ARF, we get ½ of 210°. Thus, m ∠ ARF=105°.
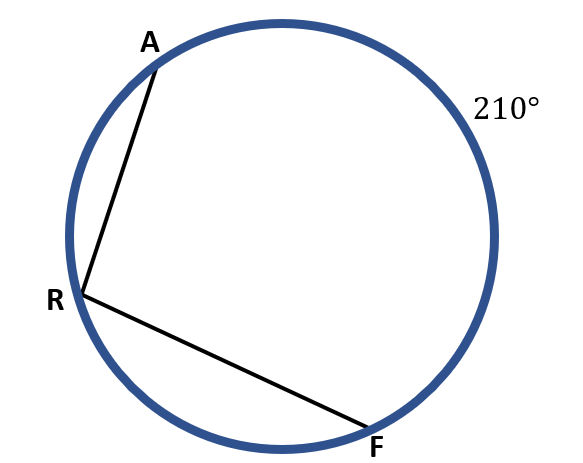
Here is the solution:
m ∠ ARF=½ m AF
m ∠ ARF=½( 210° )
m ∠ ARF=$\frac{210^o}{2}$
m ∠ ARF=105°
How do you calculate the measure of an intercepted arc of an inscribed angle?
By multiplying the inscribed angle’s measure by two or doubling it, you can get the measure of an intercepted arc from the inscribed angle.
Let us say, for instance, that the measure of the inscribed angle in the given image below is 35° or m ∠ GHI=35°. In finding the measure of the intercepted arc, GI, we get twice 35°. Hence, m GI=70°.
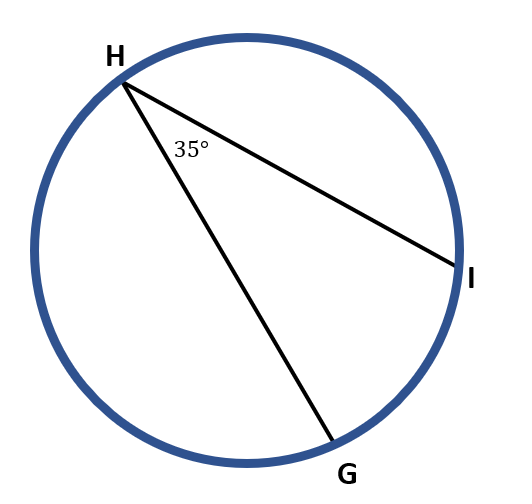
Here is the solution:
m GI=2( m ∠GHI )
m GI=2( 35° )
m GI=70°
What are the inscribed angles conjectures?
An angle is said to be inscribed if its vertex is on the circumference of the circle and both of its sides are chords of the same circle. The intercepted arc is the arc that lies in the interior of an inscribed angle and has endpoints on the angle.
The term “central angle” refers to an angle whose vertex is at the center of the circle. Its measure is equal to its intercepted arc.
The conjectures about inscribed angles are given below.
Inscribed Angle Conjectures
Inscribed Angle Conjecture
An inscribed angle in a circle has a measure that is half that of the central angle with the same intercepted arc.
Inscribed Angles Intercepting Arcs Conjecture
Two inscribed angles in a circle that share the same intercepted arc are congruent.
Inscribed Angles in a Semi-circle Conjecture
Any angle that is inscribed in a semi-circle is a right angle.
What is the measure of an angle inscribed in a semi-circle?
A 90° is the measure of an angle inscribed in a semi-circle.
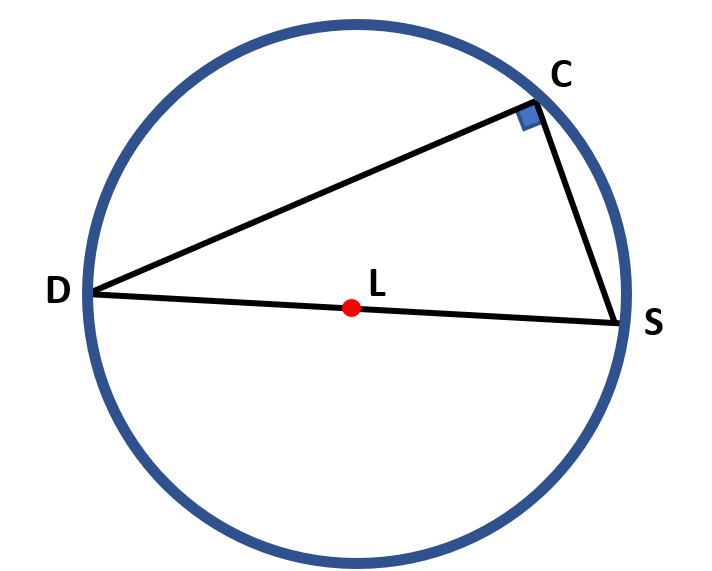
m ∠ DCS=90°
In the figure, ∠DCS is an inscribed angle, and DS is a diameter of circle L.
What is the total measure of the opposite angles of a quadrilateral inscribed in a circle?
The total measure of the opposite angles of a quadrilateral inscribed in a circle is 180°. It means that they are supplementary angles.
Let us say, for example, in the figure below, the points Q, U, A, and D form an inscribed quadrilateral. ∠Q, ∠U, ∠A, and ∠D are all inscribed angles.
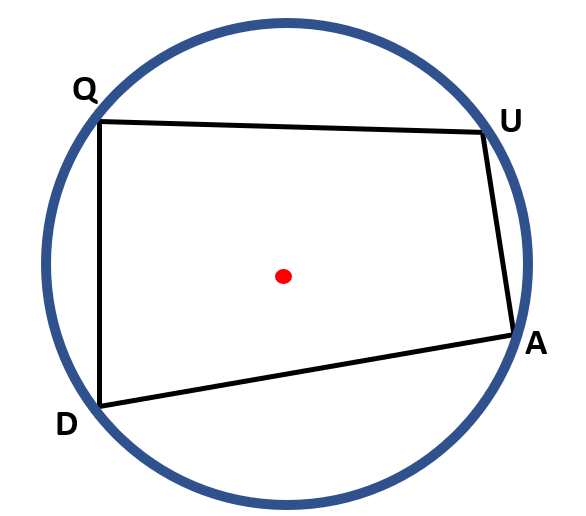
∠Q and ∠A are supplementary
∠D and ∠U are supplementary
Recommended Worksheets
Inscribed Angles (National Aviation Day Themed) Math Worksheets
Complementary Angles (Lantern Festival Themed) Math Worksheets
Adjacent Angles (Mardi Gras Themed) Math Worksheets









