Introduction
Any shape that can be divided into two equal parts that are identical to one another is said to be symmetrical. The symmetry is the line that divides the shape. One half of a symmetrical shape perfectly lies over the other half when the shape is folded along the line of symmetry, demonstrating that one half of the shape is identical to the other half. For creating symmetrical designs, understanding symmetrical shapes and lines of symmetry is highly helpful.
We will study more about symmetrical shapes, their characteristics, and some examples in this article.
What is symmetry?
Definition
Symmetry is referred to as a proportional similarity between the two halves of a shape or an object. It implies that one half is the other half’s mirror image. The term “line of symmetry” refers to the imaginary axis or line that can be used to fold a figure into its symmetrical halves. An object or shape is referred to as asymmetrical if it lacks symmetry.
An object is equal on both sides if it is symmetrical. Assume that if a handkerchief is folded such that one half of the handkerchief matches the other half, then the handkerchief shows symmetry.
Other examples of symmetry include the shapes below. You’ll see that each shape can be divided into two mirror images of one another.

What is a line of symmetry?
Definition
The term “line of symmetry” refers to the imaginary line or axis along which a figure is folded to form its symmetrical halves. In essence, it splits one thing into two mirror images. The symmetry line may run vertically, horizontally, or diagonally.
The Vertical Line of Symmetry
A vertical line of symmetry is a vertical line that divides an object or a shape into two halves. This indicates that an object is divided into its mirror halves along a vertical line that runs from bottom to top or vice versa.
The arrow below, for instance, shows a vertical line of symmetry. The vertical line of symmetry allows us to see that the arrow’s left and right halves are precisely the same.
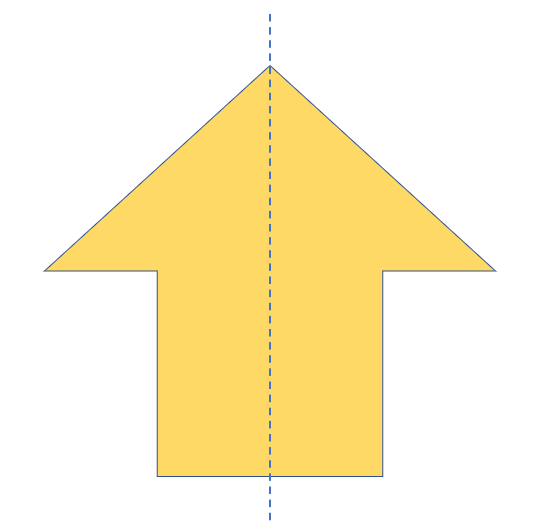
The Horizontal Line of Symmetry
A horizontal line that divides an object or shape into two halves is known as a horizontal line of symmetry. Specifically, it refers to the division of an object or shape into its mirror images along a horizontal axis that runs from right to left or vice versa.
The square is divided in half by the horizontal line of symmetry shown below. The shape’s upper and bottom halves are equal because of the horizontal line of symmetry that passes through it from left to right or vice versa.
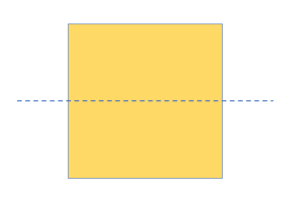
The Diagonal Line of Symmetry
A diagonal line of symmetry is a line that divides an object or shape into two equally sized halves. This implies that the slanting line splits the object or shape into its mirror images.
The image below shows a circle’s diagonal line of symmetry. The two halves are identical to one another, as shown in the illustration.
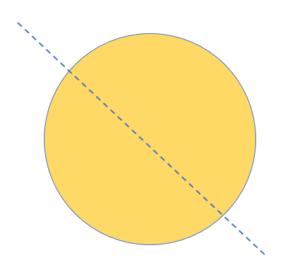
What are symmetrical shapes?
Definition
If a shape can be divided into two equal pieces with both sides being exactly the same, it is said to be symmetrical. One half of a symmetrical shape exactly lies over the other half when it is folded along the line of symmetry, demonstrating that the two halves of the shape are identical.
There are symmetrical shapes as well as asymmetrical shapes. Regular and irregular shapes may be symmetrical. Some shapes may have one line of symmetry, while others may have two, and still, others may have three or more lines of symmetry. A shape does not have a line of symmetry if it is not symmetrical.
Shapes with one line of symmetry
Let us look at the shapes below with one line of symmetry.
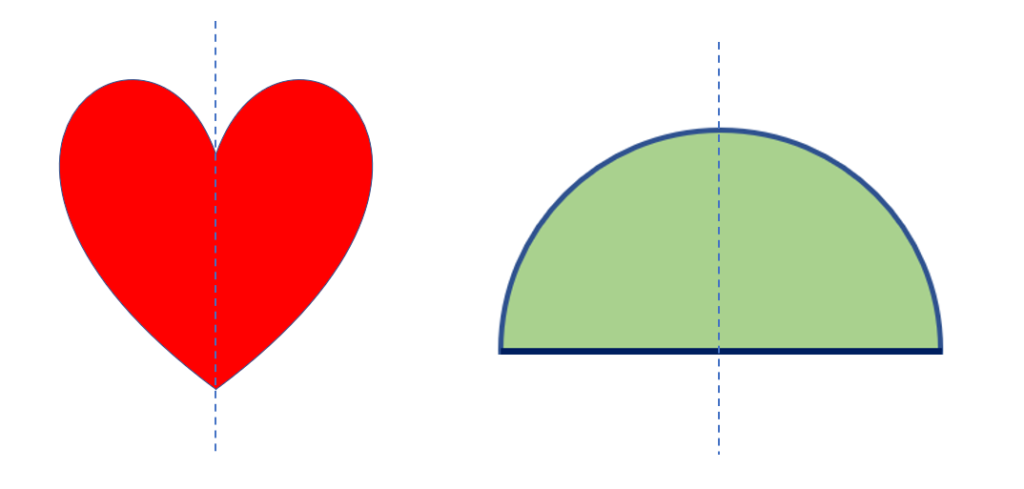
As seen in the illustration, the semicircle and the heart have a single line of symmetry. With a vertical line of symmetry, they are symmetrical. These shapes cannot be divided evenly along horizontal or diagonal lines that will have identical parts. As a result, each shape has one line of symmetry.
Shapes with two lines of symmetry
There are shapes with two symmetrical lines. These shapes might have symmetrical lines that go vertically and horizontally, diagonally and vertically, etc. Let us have a rectangle as our first example of a shape with two lines of symmetry.
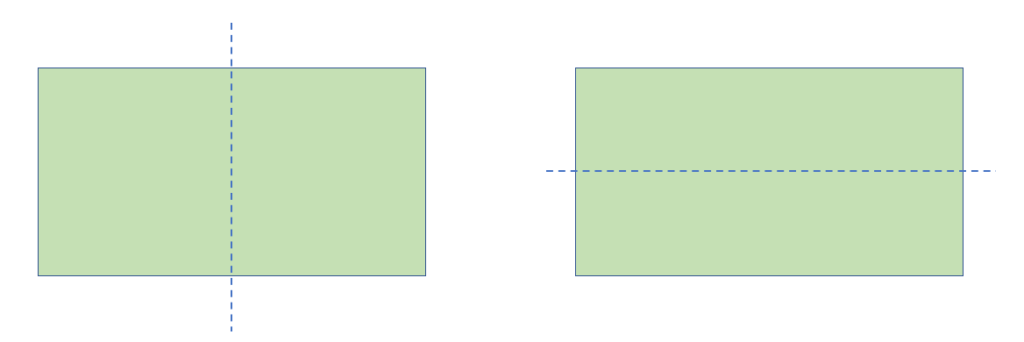
As seen in the illustration, a rectangle has two lines of symmetry: a vertical line and a horizontal line. The rectangle’s left and right halves are identical in size due to the vertical line of symmetry. The upper half of the rectangle matches the lower half of the rectangle along the horizontal line of symmetry.
You might be wondering if a rectangle has a vertical line of symmetry. Let us look at the illustration below.

Since the parts of the rectangle do not mirror images of one another when folded, using a diagonal to divide the rectangle does not show symmetry.
The letter H is another example of a form with two lines of symmetry.

The shape’s two symmetry lines, which are vertical and horizontal, are visible. The image is divided into two identical, mirror-image halves by both lines.
Shapes with three or more lines of symmetry
Some shapes have three or more lines of symmetry. Let’s use the images below as samples. We can find more than two lines of symmetry in a triangle, a square, and a circle.

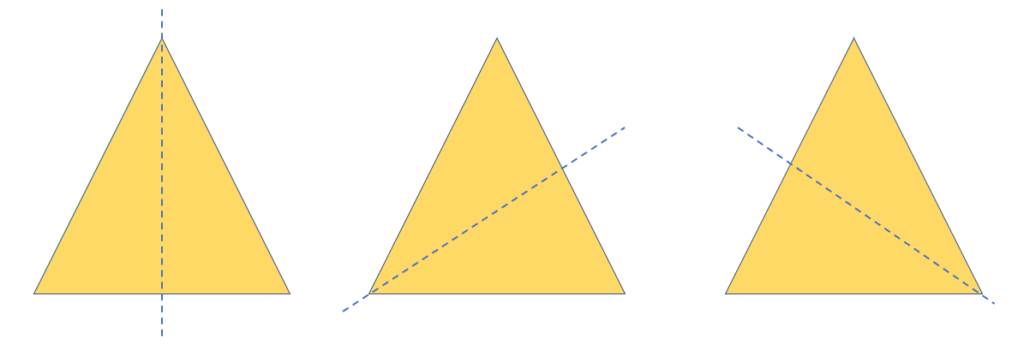
Let’s start with the triangle that is shown. In the triangle, there are three symmetry lines. These lines of symmetry are shown in the image below. Every line divides the triangle into two equally sized, mirror-image halves.
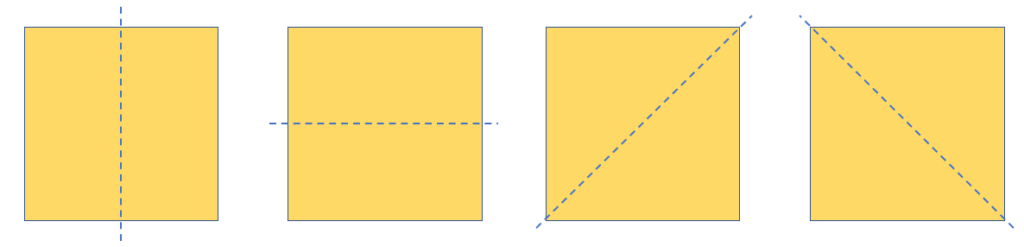
A square has four lines of symmetry: a vertical line, a horizontal line, and diagonal lines. The illustration below shows how these lines divide a square in half and create symmetry.
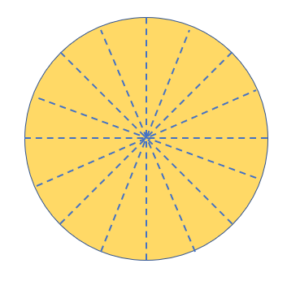
There are an endless number of lines of symmetry in a circle. A circle’s infinite diameters, which separate it into semicircles, result in an infinite number of lines of symmetry. In the picture below, a circle with several symmetry lines is shown.
Shapes with no line of symmetry
There are also clearly defined shapes that lack symmetry lines or cannot be separated into two parts that end up reflecting one another. Scalene triangles, parallelograms, and trapezoids are a few examples of these shapes. These shapes can be seen in the image below.
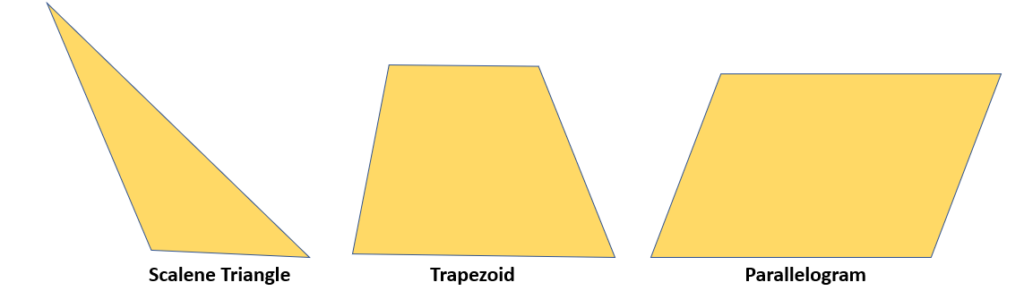
Symmetry in Regular Shapes
Angles and sides of regular shapes have the same measurements. In general, regular shapes show symmetry, and the number of lines of symmetry in a regular shape is equal to the number of sides. The properties of regular shapes and how many lines of symmetry each shape are shown in the table below.
| Regular Shapes | Number of Sides | Lines of Symmetry | Illustration |
| Equilateral Triangle | 3 sides | 3 lines of symmetry |  |
| Square | 4 sides | 4 lines of symmetry |  |
| Regular Pentagon | 5 sides | 5 lines of symmetry | 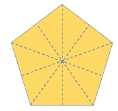 |
| Regular Hexagon | 6 sides | 6 lines of symmetry | 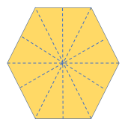 |
| Regular Heptagon | 7 sides | 7 lines of symmetry | 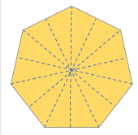 |
| Regular Octagon | 8 sides | 8 lines of symmetry | 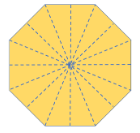 |
| Regular Decagon | 10 sides | 10 lines of symmetry | 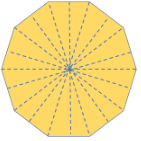 |
| Regular Dodecagon | 12 sides | 12 lines of symmetry | 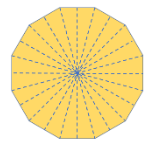 |
Symmetry in Irregular Shapes
Most irregular shapes lack a line of symmetry. There are, nevertheless, some irregular shapes that have one or two symmetry lines. Some examples of irregular shapes that are symmetrical are isosceles triangle, rhombus and rectangle. A rectangle and a rhombus both have two lines of symmetry, whereas an isosceles triangle only has one.
More Examples
Example 1
Find the total number of symmetry lines in each of the shapes below.
( a ) | ( b ) | ( c ) |
Solution:
( a ) The heart shape has just one line of symmetry. The shape is divided into two identical, mirror-image halves by a vertical line of symmetry.
( b ) The image is a regular hexagon. The number of symmetry lines for a regular shape is equal to the number of sides. There are, therefore, six lines of symmetry in a regular hexagon.
( c ) Given that the pentagon has five unevenly spaced-out sides, the illustration shows an irregular pentagon. The irregular shape is split into two identical halves by a single vertical line of symmetry.
Example 2
Identify if the given shape is symmetric or asymmetric.
( a )  | ( b ) | ( c ) |
Solution:
( a ) The given shape is symmetric with a vertical line of symmetry.
( b ) The arrow shape is symmetric with a horizontal line of symmetry.
( c ) The shape is asymmetric, which means that the shape does not have a line of symmetry.
Example 3
Determine whether the shape is symmetrical or not. Find the total number of lines of symmetry if the shape is symmetrical.

Solution:
Given its twelve sides, the shape is an irregular dodecagon. There are four lines of symmetry in shape. The figure below displays the lines of symmetry.
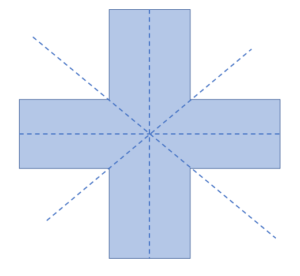
Example 4
Which of these letters is symmetrical along a vertical axis?
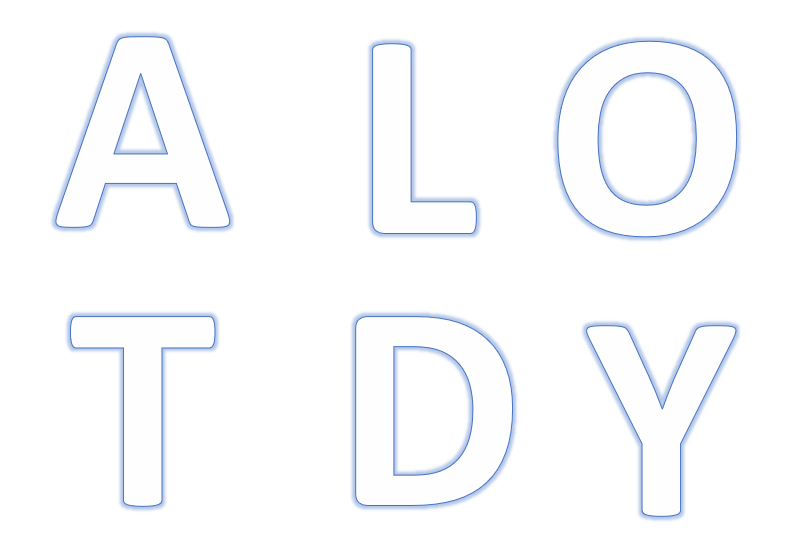
Solution:
Each of the letters A, O, T, and Y has a vertical line of symmetry. The graphic below shows the vertical symmetry lines that divide each letter into two halves that mirror one another.
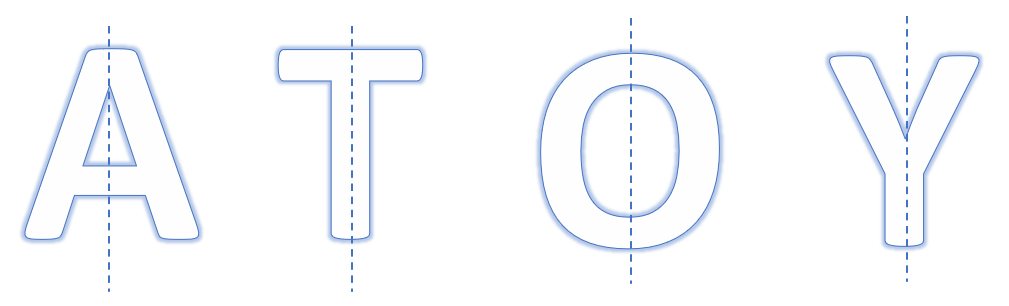
On the other hand, the letter L lacks a line of symmetry while the letter D has a horizontal line of symmetry.
Summary
Symmetry is referred to as a proportional similarity between the two halves of a shape or an object. It implies that one half is the other half’s mirror image.
The term “line of symmetry” refers to the imaginary line or axis along which a figure is folded to form its symmetrical halves. In essence, it splits one thing into two mirror images. The symmetry line may run vertically, horizontally, or diagonally.
If a shape can be divided into two equal pieces with both sides being exactly the same, it is said to be symmetrical.
Both regular and irregular shapes can be symmetrical. While some shapes may have one line of symmetry, some may have two; others still may have three or more; there are also shapes that lack a line of symmetry. Most irregular shapes are asymmetrical due to their uneven sides. The number of symmetry lines in a circle is infinite.
The number of symmetry lines and the number of sides is equal for regular shapes. For instance, a square has four lines of symmetry, a pentagon has five lines, a hexagon has six lines, a heptagon has seven lines, an octagon has eight lines, a decagon has ten lines, and a dodecagon has twelve lines of symmetry.
An isosceles triangle is one of the irregular shapes with one line of symmetry, whereas a rectangle and a rhombus have two lines of symmetry.
Frequently Asked Questions on Symmetrical Shapes ( FAQs )
What is meant by symmetry in Mathematics?
There is symmetry not only in geometry but also in other areas of mathematics. However, symmetry is frequently used in geometry, where it is defined as a proportional similarity between the two sides of a shape or object. It suggests that one half is the mirror image of the other.
To be referred to as symmetrical, two objects must be identical in terms of size, shape, and orientation. A square is an example of a regular shape that has symmetry. The left side of a square is a mirror image of the right side, as can be seen, if you draw a vertical line of symmetry through it. If objects do not have a line of symmetry, it is referred to as asymmetric.
What makes a two-dimensional (2D) shape symmetrical?
If a line could be drawn across a two-dimensional (2D) object and either side is a reflection of the other, then the shape is said to be symmetrical. The line is known as a line of symmetry. A line of symmetry can also be called a ‘mirror line’.
A two-dimensional (2D) shape is symmetrical if one half of the shape is a mirror of the other half. They must be identical in terms of size, shape and orientation with respect to another.
Some symmetrical two-dimensional (2D) shapes are square, rectangle, circle, equilateral and isosceles triangles, etc.
What is meant by the line of symmetry?
The term “line of symmetry” refers to the imaginary line or axis along which a figure is folded to form its symmetrical halves. In essence, it splits one thing into two mirror images. The symmetry line may run vertically, horizontally, or diagonally.
Shapes can have one line of symmetry, two lines of symmetry, three lines of symmetry, or more. They can also have no lines of symmetry. A circle is an example of a shape that has an infinite number of lines of symmetry, while a scalene triangle is an example of a shape that does not have a line of symmetry.
Regular shapes—those with sides and angles of the same measure—are symmetrical, and the number of their symmetry lines equals the number of sides. A square, for instance, has four sides and four lines of symmetry. Regular pentagons have five symmetry lines, regular hexagons have six symmetry lines, regular heptagons have seven symmetry lines, regular octagons have eight symmetry lines, and regular decagons have ten symmetry lines.
What are some examples of symmetrical shapes?
There are lots of different shapes that are symmetrical. The following are examples of symmetrical shapes.
Equilateral Triangle. This is a regular shape with equal sides, angles and three lines of symmetry.
Isosceles Triangle. This is an irregular shape with 2 sides having the same measurement and one line of symmetry.
Square. This is a regular shape with 4 equal sides, four angles that measure 90 degrees and four lines of symmetry.
Rectangle. This is an irregular shape with four sides (opposite sides are congruent), four angles and two lines of symmetry.
Regular Pentagon. This is a regular shape with 5 sides and angles equal in measurement and 5 lines of symmetry.
Regular Hexagon. This is a regular shape with six sides and angles equal in measurement and six lines of symmetry.
Regular Pentagon. This is a regular shape with seven sides and angles equal in measurement and seven lines of symmetry.
Regular shapes often have symmetry, with the number of symmetry lines equals the number of sides. As a result, a regular hexagon has six lines of symmetry, a regular octagon has eight, a regular decagon has 10, and so forth.
What are asymmetrical shapes?
The opposite of symmetrical is asymmetrical. It should be simple to understand that asymmetrical means that the two sides of any object or shape are different since symmetrical implies that the two sides of an object or shape are identical. Shapes that are asymmetrical are uneven, crooked, and don’t fold precisely in two.
As an example, let us have the triangles below.

The triangle on the left is equilateral, while the triangle on the right is scalene. The equilateral triangle has sides of equal length, while the scalene triangle has uneven side lengths.
The equilateral triangle is symmetrical and has three lines of symmetry, while the scalene triangle does not have a line of symmetry.
How many lines of symmetry do quadrilaterals have?
A quadrilateral is a four-sided, two-dimensional shape. Different quadrilateral types have varying numbers of lines of symmetry. The properties of various quadrilaterals and their lines of symmetry are shown in the table below.
| Quadrilateral | Sides | Angles | Line of Symmetry |
| Square | Four equal sides Opposite sides are parallel | Four equal angles that measure 90 degrees | Four lines of symmetry |
| Rectangle | Two pairs of equal sides Opposite sides are parallel | Four equal angles that measure 90 degrees | Two lines of symmetry |
| Parallelogram | Two pairs of equal sides Opposite sides are parallel | Opposite angles are equal | No line of symmetry |
| Rhombus | Four equal sides Opposite sides are parallel | Opposite angles are equal | Two lines of symmetry |
| Kite | Two pairs of equal sides | One pair of equal angles | One line of symmetry |
How many lines of symmetry must a shape have to be symmetrical?
A shape can be symmetrical with just one line of symmetry.
Why is learning symmetry important?
In geometry, symmetry is a fundamental concept. It generates patterns that assist in organizing the environment around us. Artists, vocalists, choreographers, engineers, mathematicians, and others who work in the creative industries use symmetry.
It is essential for students to understand geometry and symmetry to introduce them to daily objects that aren’t directly related to mathematics but have a solid mathematical foundation.
What are the four types of symmetry?
Rotational, translational, reflexive, and glide are the four types of symmetry.
Radial symmetry is another name for rotational symmetry. When a form or pattern maintains its appearance after being rotated by a fraction of a turn, it displays rotational symmetry. The number of turns it takes for a shape to keep the same appearance is how we determine rotational symmetry.
For instance, a square still looks the same after being rotated by 90 degrees. If a rectangle were rotated 180 degrees, it would still look the same.
Recommended Worksheets
Symmetrical Shapes (Bodhi Day Themed) Math Worksheets
Regular and Irregular Shapes (World Oceans Day Themed) Math Worksheets
Basic Shapes (International Day of PWD’s Themed) Math Worksheets









