Pascal’s Triangle

Introduction

Mathematics is a world of numbers. We have different sets of numbers that can be arranged in different sequences and patterns. One such arrangement of numbers is the Pascal’s triangle. What is it and who invented it? Let us find out.

Definition

Pascal’s Triangle is the triangular arrangement of numbers that gives the coefficients in the expansion of any binomial expression. The numbers are so arranged that they reflect as a triangle. We can also say that Pascal’s triangle is an arrangement of binomial coefficients in triangular form. The numbers in Pascal’s triangle are placed in such a way that each number is the sum of two numbers just above the number.  

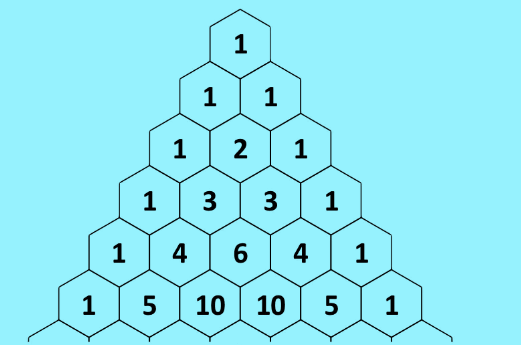
Who Invented Pascal’s Triangle?

Blaise Pascal was born on June 19, 1623, at Clermont-Ferrand, in the Auvergne region of France. Pascal triangle as we know it today was originally written as the Treatise on the Arithmetical Triangle by Blaise Pascal in 1653. Although in the eleventh century mathematicians from Persia and China had independently discovered the triangle, most of the properties and applications of this triangle were discovered by Pascal. This was not the only contribution of Pascal to the world of mathematics. He also derived significant theorems in geometry, invented the Pascaline calculator and discovered the foundations of Calculus and probability. However, Pascal’s triangle is regarded as his best contribution to mathematics.

Construction of Pascal’s Triangle

The following are the steps involved in the construction of Pascal’s triangle – 

1. Starting with row zero and writing only the number one is the easiest way to construct a pascal Triangle.
2. The next step is to obtain the numbers in the subsequent rows. The pattern followed here is that we add the number directly above and to the left of the number with the number above and to the right of it.
3. If there are no numbers on the left or right side, replace a zero for that missing number and proceed with the addition.

Let us understand the construction of the Pascal’s triangle. Here is what a Pascal’s triangle looks like – 

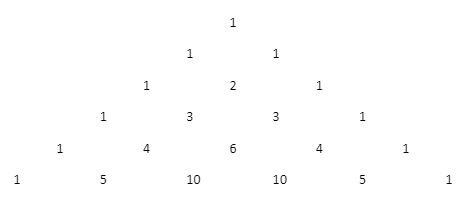
Notice the first row. We have placed a 1 in the first row. 

Next, in the second row, we can see that there are two 1 digits. It is important to note here that since there was no number to the left or to the right of the digit 1 in the first row, therefore, it would be carried down as it is without any additions.  

The third row gives a better understanding of the additions involved in Pascal’s triangle. We can notice that there is a number 2 in the third row that lies between the two 1 ‘s we had in the second row. We know that 1 + 1 = 2. This sum of the two numbers in the previous row is placed at the centre of the numbers below them. The positioning of the 1 digits in the third is similar to what we did in the second row. This means that since there was no number to the left or to the right of the digit 1s in the second row in the second row, therefore, it would be carried down as it is without any additions. 

Now, observe the fourth row, we can see a digit 4 that lies between the digits 1 and 3 which are placed on the third row. We know that 1 + 3 = 4. Similarly, the digit 6 is placed between the digits 3 and 3 which are placed on the third row. We know that 3 + 3 = 6. Again, we have a digit 4 that lies between the digits 1 and 3 which are placed on the third row. We know that 1 + 3 = 4. The outer ends of the row remain 1 only as there is no number to the left or to the right of the digit 1 in the third row. Subsequent rows are thus created in this manner.

Properties of Pascal’s Triangle

The following are the properties of a Pascal’s triangle – 

1. Each digit in the Pascal’s triangle is actually the sum of the two numbers that lie above it. This number is placed between the above lying numbers in the next row.
2. The outside numbers of the Pascal’s triangle are all 1.
3. The Pascal’s triangle is symmetric in appearance due to the specific arrangement of digits.
4. The first diagonal of the Pascal’s triangle shows the counting numbers.
5. The sums of the rows of the Pascal’s triangle give the powers of 2. For example, in the 4th row of the Pascal’s triangle, the numbers are 1 4 6 4 1. The sum of all these numbers will be 1 + 4 + 6 + 4 + 1 = 16 = 2 ⁴.
6. Each row of the Pascal’s triangle gives the digits of the powers of 11.
7. By adding the different diagonal elements of a Pascal’s triangle, we get the Fibonacci series.  
8. If a row has the second element a prime number, then all the following elements in the row are divisible by that prime number (not including the 1 s). for example, if we look at row 5, it contains the numbers, (1 5 10 10 5 1). We can see that 5 and 10 are divisible by 5. However, for a composite numbered row, such as row 8 (1 8 28 56 70 56 28 8 1), 28 and 70 are not divisible by 8.
9. The elements in the Pascal’s triangle can find out by finding the sum of the two adjoint elements in the preceding row.

The Formula of Pascal’s Triangle

How do we find out numbers placed on any sequence of the Pascal’s triangle? Is there any formula for it? Let us find out.

Let the rows of a Pascal’s triangle be represented by “ n “ and the columns of a Pascal’s triangle be represented by “ k “. So, the formula to find the entry of an element in the nth row and kth column of a pascal’s triangle is given by – 

( n k ) = ( n-1  k-1 ) + ( n-1 k )

Here, n is a non-negative integer and k lies between and n. this means that n ≥ 0 and 0 ≤ k ≤ n.

The above formula can also be written as  – 

ⁿ C _k = $\frac{n!}{k!(n-k)!}$

Let us understand the above formula by an example.

Example

Suppose we want to find the 3 rd element in the 5^th row of a Pascal’s triangle. How will we use the above formula to find it?

Solution

We are required to find the 3 rd element in the 5^th row of a Pascal’s triangle. This means that we need to find out the value of ⁵ C ₃.

We know that 

( n k ) = ( n-1  k-1 ) + ( n-1 k )

Here we have n = 5 and k = 3. So, substituting the values of n and k in the above equation we get,

 ( 5 3 ) = ( 5-1  3-1 ) + ( 5-1 3 )

⇒  ( 5 3 ) = ( 4  2 ) + ( 4  3 )

So, this means we need to add the 2 nd element in 4 th row ( which is 4 ) with 3rd element in 4 rd row (which is 6).

Hence, we have, ( 5 3 ) = 4 + 6 = 10

Use of Pascal’s Triangle in Probability

Pascal’s triangle finds its use in a number of applications in mathematics. For example, Pascal’s triangle is extensively used in Probability to find the possible number of outcomes of a given situation. For instance, the number of combinations of heads or tails that are possible from the number of process can be obtained using a Pascal’s Triangle. The below table demonstrates different results that can be obtained using a Pascal’s triangle, when a coin is tossed and number of times – 

Rows of Pascal’s Triangle	Outcomes	Numbers in Pascal’s Triangle
1	{ H }, { T }	1 , 1
2	{ H H }, {H T, T H}, {T T}	1, 2, 1
3	{ H H H }, { H H T , H T H , T H H }, { H T T , T H T , T T H }, { T T T }	1, 3, 3, 1
4	{ H H H H }, { H H H T , H H T H , H T H H, T H H H }, { H H T T, H T H T,  H T T H , T H H T ,  T H T H ,   T T H H }, { H T T T ,   T H T T ,   T T H T , T T T H }, { T T T T }	1, 4, 6, 4, 1

Pascal’s Triangle and Binomial Expansion

The coefficients that appear in the binomials expansions can be defined by the Pascal’s triangle as well. This means the n th row of Pascal’s triangle comprises the coefficients of the expanded expression of the polynomial (x + y) ⁿ. We know that a binomial expansion is defined as – 

 ( x + y) ⁿ = a ₀ x ⁿ + a ₁ x ^{n – 1} y + a ₂ x ^{n – 2} y ² + a ₃ x ^{n – 3} y ³ … + a _{n – 1} x y ^{n – 1} + a _n y ⁿ

The coefficients of a _k in the above formula are exactly the same elements that we have in a Pascal’s triangle.

This means that

a _k = ($\frac{n}{k}$)

Let us understand it using an example.

Example

Let us expand the binomial expansion for n = 4, i.e. let us expand the expression ( x + y ) ⁿ for n = 4.

We will have,

( x + y ) ⁴ = ⁴ C ₀ x ⁴ + ⁴ C ₁ x ³ y + ⁴ C ₂ x ² y ² + ⁴ C ₃ x y ³ + ⁴ C ₄ x ⁰ y ⁴

⇒( x + y ) ⁴ = ( 1 ) x ⁴ + ( 4 ) x ³ y + ( 6 ) x ² y ² + ( 4 ) x y ³ + ( 1 ) x ⁰ y ⁴

Note the coefficients of all the terms in the above expansion. We have, 1 , 4 , 6, 4, 1. These are the same terms that represent the 4 th row of a Pascal’s triangle. Hence we can say that the coefficients of a _k in the binomial expansion are exactly the same elements that we have in a Pascal’s triangle.

Examples

Example 1 Expand ( x + y )³ using Pascal’s triangle.

Solution Let us find the value of ( x + y )³ using Pascal’s triangle. 

Exponent	Pascal’s Triangle
0	1
1	1     1
2	1       2          1
3	1         3         3        1

From the above we can see that the coefficient’s of the expansion ( x + y )³ will be 1, 3, 3 1.  

Let us now verify the same using the formula of the binomial expansion.

We know that – 

( x + y) ⁿ = a ₀ x ⁿ + a ₁ x ^{n – 1} y + a ₂ x ^{n – 2} y ² + a ₃ x ^{n – 3} y ³ … + a _{n – 1} x y ^{n – 1} + a _n y ⁿ

Therefore, we have,

( x + y ) ³ =  ³ C ₀  x ³ + ³ C ₁ x ² y + ³ C ₂ x y ² + ³ C ₃ x ⁰ y ³

= ( 1 ) x ³ + ( 3 ) x ² y + ( 3 ) x y ² + ( 1 ) y ³

We can see that the coefficients of the expansion ( x + y )³ will be 1, 3, 3 1 which are the same that were obtained using the Pascal’s triangle.

Example 2 A coin is tossed three times, find the probability of getting exactly 2 tails using Pascal’s triangle.

Solution We have been given that a coin is tossed three times. We need to find the probability of getting exactly 2 tails using Pascal’s triangle.

We know that the formula for Pascal’s triangle is given by

( n k ) = ( n-1  k-1 ) + ( n-1 k )

Using the above formula, we can see that the total number of outcomes will be the sum of coefficients in the 3 rd of the Pascal’s triangle, i.e. 1 + 3 + 3 + 1 = 8 

Also, 2 ³ = 8 , where 3 of them give exactly two tails.

Hence, the probability of getting exactly two tails is 3/8, or 37.5%

Key Facts and Summary

1. Pascal’s Triangle is the triangular arrangement of numbers that gives the coefficients in the expansion of any binomial expression. The numbers are so arranged that they reflect as a triangle.
2. Each digit in the Pascal’s triangle is actually the sum of the two numbers that lie above it. This number is placed between the above lying numbers in the next row.
3. The outside numbers of the Pascal’s triangle are all 1.
4. The Pascal’s triangle is symmetric in appearance due to the specific arrangement of digits.
5. The first diagonal of the Pascal’s triangle shows the counting numbers.
6. The sums of the rows of the Pascal’s triangle give the powers of 2. For example, in the 4th row of the Pascal’s triangle, the numbers are 1 4 6 4 1. The sum of all these numbers will be 1 + 4 + 6 + 4 + 1 = 16 = 2 ⁴.
7. Each row of the Pascal’s triangle gives the digits of the powers of 11.
8. By adding the different diagonals elements of a Pascal’s triangle, we get the Fibonacci series.  
9. If a row has the second element a prime number, then all the following elements in the row are divisible by that prime number (not including the 1 s). for example, ex. 1 5 10 10 5 1.
10. The elements in the Pascal’s triangle can find out by finding the sum of the two adjoint elements in the preceding row.
11. The formula to find the entry of an element in the nth row and kth column of a pascal’s triangle is given by ( n k ) = ( n-1  k-1 ) + ( n-1 k ), where n is a non-negative integer and k lies between and n. this means that n ≥ 0 and 0 ≤ k ≤ n.
12. Pascal’s triangle is extensively used in Probability to find the possible number of outcomes of a given situation.
13. The coefficients of a _k in the binomial expansion are exactly the same elements that we have in a Pascal’s triangle.