Introduction
Three-dimensional (3D) objects have several flat surfaces (faces) made of polygons that are connected by edges and corners (vertices). These solid shapes’ ability to be represented in two dimensions by a shaped net is useful, especially in getting its surface area.
Let us say, for instance, a flat corrugated paper box will be in its three-dimensional shape upon folding up its 2D net. This is just an immediate example of the use of geometric nets, but it offers other important applications.
Understanding how a three-dimensional shape is constructed from two-dimensional parts is important for every aspect of three-dimensional design, not just when building boxes. Engineers and developers use powerful and advanced computer-aided design (CAD) software to assist in their work. The vital spatial skills you acquire from a foundational understanding of form nets can thus develop further into other more challenging design applications.
In this article, we will define geometric nets, learn various net shapes, determine whether a net constitutes a solid, and calculate the surface area and volume of a shape from the perspective of its geometric net.
What are Geometric Nets?
Definition
A geometric net refers to a two-dimensional shape that can be modified to create a solid or a three-dimensional shape. A geometric net pattern is produced when the surface of a three-dimensional figure is spread out flat, and each face is visible.
How to determine if a net forms a solid
These are the conditions to be met if a net forms a solid or a three-dimensional shape:
( 1 ) Make sure that both the solid and the net have the same number of faces and that the solid’s faces correspond to the same faces in the net in terms of shape.
( 2 ) Make sure that all the sides fit together properly by picturing how the net will be folded to create the solid.
As a recall, three-dimensional (3D) shapes take up space. They have height, length, and width. They are all objects that we can hold, such as a pencil, phone, table, boxes, ball, etc.
There are characteristics shared by all three-dimensional shapes. Among these qualities are faces, edges, and corners.
| A flat surface makes up the face of a three-dimensional shape. The faces frequently take on 2D shapes. The edge of a surface is the line separating two of its surfaces. Two or more edges meet to form a corner. A corner is also referred to as a vertex. |
Nets of Three-dimensional (3D) Shapes
A 3D shape’s “net”—also referred to as its geometry net—is what it would look like if it were opened and placed flat. A 3D shape would resemble a net if it were to be unfolded. To create 3D shapes, you can sketch and fold nets.
Examples of common geometric nets include cube, cuboid or rectangular prism, triangular prism, a tetrahedron ( triangular-based pyramid), square-based-pyramid, cylinder, and cone.
Net of a Cube
Six identical square faces make up the three-dimensional shape of a cube.
One of the easiest to visualize is cube nets, and seeing how many you can construct is a great exercise in spatial reasoning.
Net of a Cube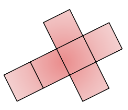 | A cube |
Six squares combine to make a cube with six faces, twelve edges, and eight vertices.
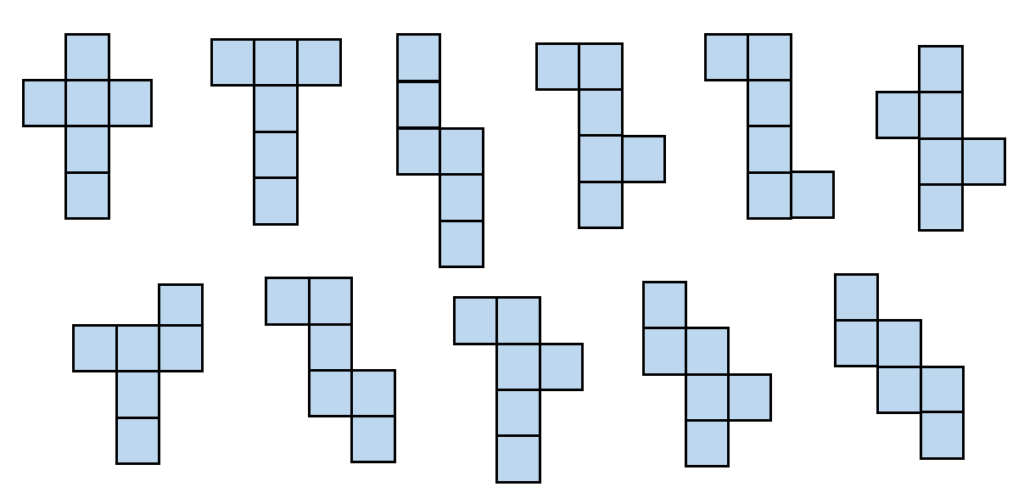
Eleven different geometric nets form a cube. The figures below show the 11 possible nets for a cube.
Net of a Rectangular Prism
A rectangular prism is a shape that resembles a cube, although one or more of its sides could be rectangular. Thus, the nets have similar traits to those of a cube yet have distinct appearances. Six rectangles make up a rectangular prism.
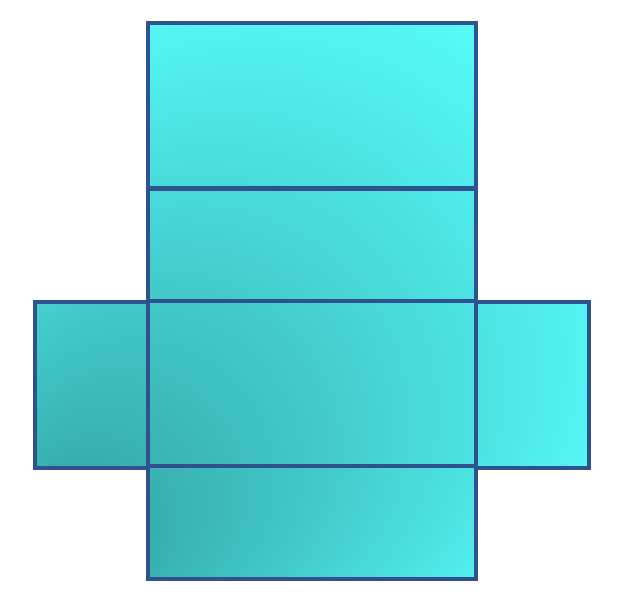
A rectangular prism has six ( 6 ) faces twelve (12 ) edges, and eight ( 8 ) vertices.
Net of a Triangular Prism
A polyhedron with two triangle bases and three rectangle sides is known as a triangular prism. It is a three-dimensional shape with two base faces, three side faces, and connections at the edges. A triangular prism is made up of three rectangles and two triangles.
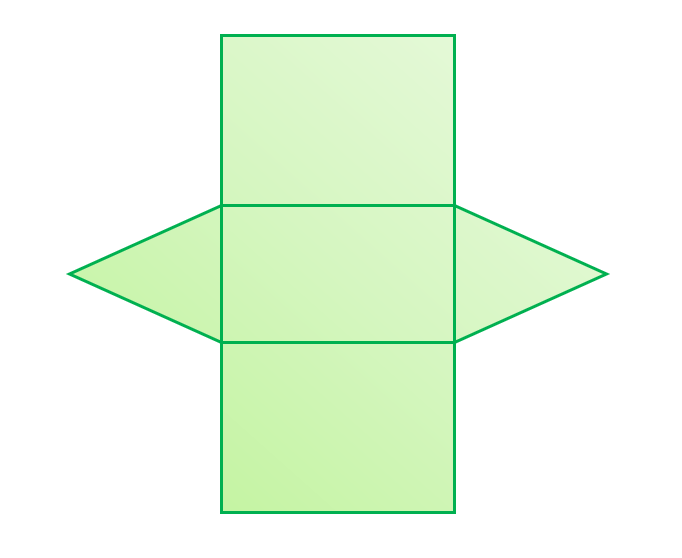
A triangular prism has five ( 5 ) faces nine (9 ) edges, and six ( 6 ) vertices.
Net of a Square-Based Pyramid
A square-based pyramid has a base that is square and faces that are triangular and meet at a vertex above the base. A square-based pyramid is made up of a square and four isosceles triangles.

A square-based pyramid has five ( 5 ) faces eight (8 ) edges, and five ( 5 ) vertices.
Net of a Tetrahedron / Triangular-based Pyramid
A tetrahedron or triangular-based pyramid is a pyramid with a triangular base and three triangular sides. The image below shows the net of a triangular-based pyramid made up of four triangles.
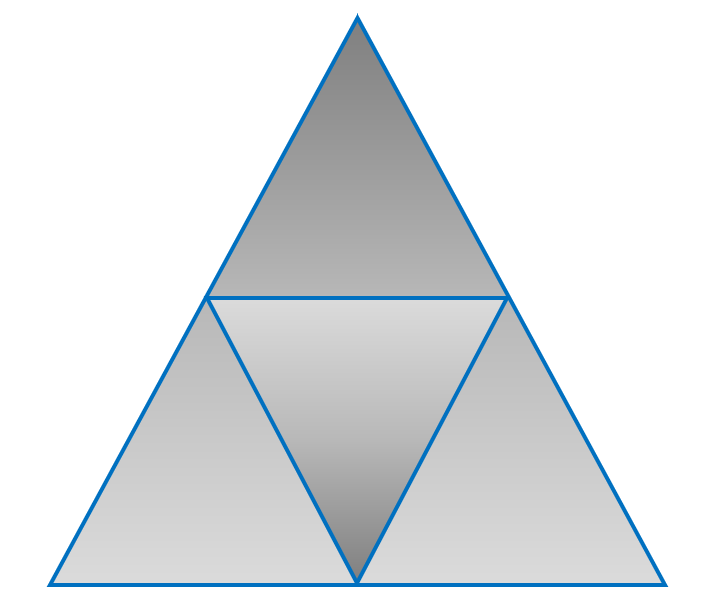
A Tetrahedron / Triangular-based Pyramid has four ( 4 ) faces six (6 ) edges, and four ( 4 ) vertices.
Net of a Cylinder
The three-dimensional shape of a cylinder consists of two identical circular bases connected by a curved surface. The cylinder’s net is composed of a single rectangle and two circles.
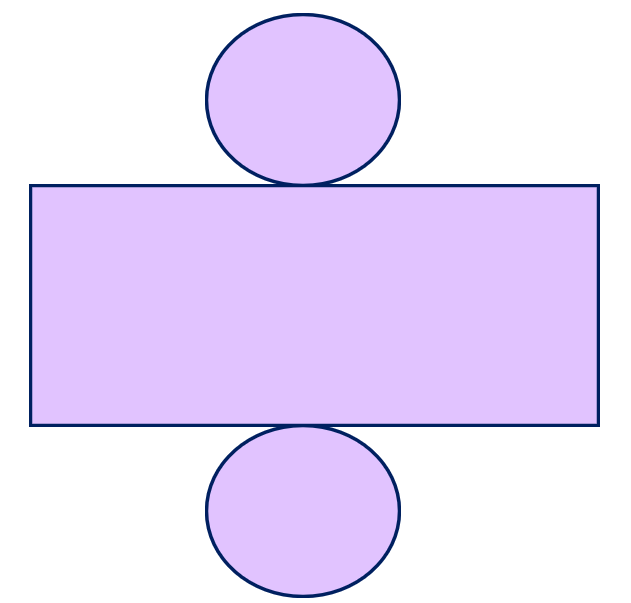
A cylinder has three ( 3 ) faces two (2 ) edges, and zero ( 0 ) vertices.
Net of a Cone
A cone’s geometric form consists of a circular base and a curved surface that tapers from the base to a point known as the vertex.

A cone has two (2 ) faces one (1 ) edge, and one ( 1 ) vertex.
How to Calculate Surface Area Using Nets
Example 1
Calculate the surface area of the geometric net shown below.
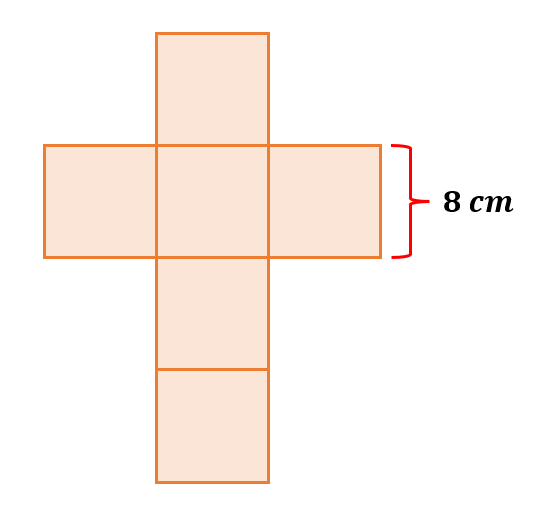
Solution:
The image shows a net of a cube. To calculate its surface area, we must first get the surface of a face and then multiply the value to 6 since a cube has six faces. It is also given that each side of the square measures 8 cm.
Area of a square=s2
Area of a square =( 8 cm )2
Area of a Square=64 cm2
Calculating the total surface area of the six faces of the cube we may have,
Surface Area of a Cube=6s2
Surface Area of a Cube=6 ( 64 cm2 )
Surface Area of a Cube=384 cm2
Example 2
A square-based pyramid is shown below; find its surface area.
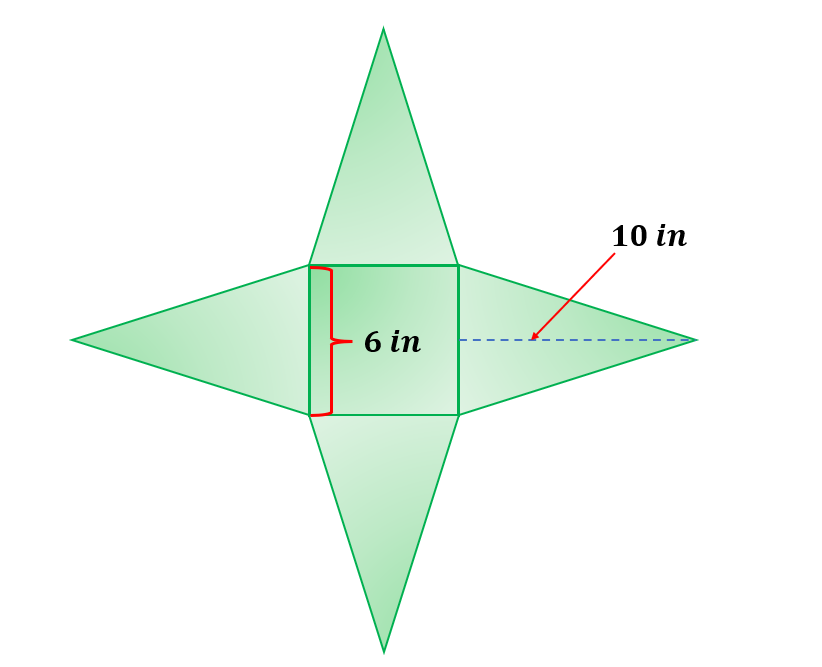
Solution:
To solve the surface area of the given square-based pyramid, we must get the area of the base, which is a square, and the total area of the four triangles. The given net of a square-based pyramid has a base with 6 in. on each side, while the height of the triangle is 10 in.
| For the area of the square: Area of a Square=s2 Area of a Square=( 6 in )2 Area of a Square=36 in2 | For the area of a triangle: Area of a Triangle=½bh Area of a Triangle=½( 6 in )( 10 in ) Area of a Triangle=½( 60 in2 ) Area of a Triangle=60/2 in2 Area of a Triangle=30 in2 |
To solve the total surface area of the square-based pyramid, we may have,
Surface Areasquare-based pyramid
=AreaSquare + 4 ( Areatriangle )
=36 in2+4 ( 30 in2 )
=36 in2+120 in2
=156 in2
Therefore, the square-based pyramid has a surface area of 156 in2.
Example 3
Using the figure below, find the surface area of the rectangular prism.
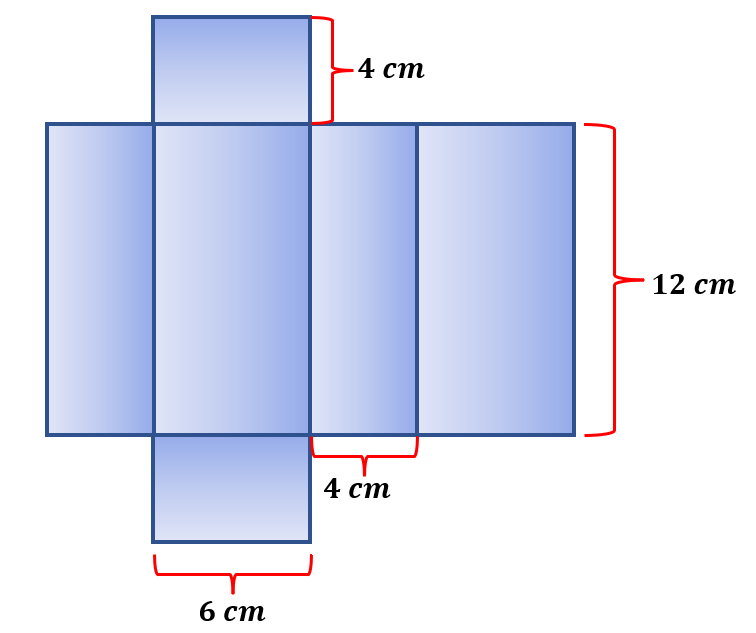
Solution:
The rectangular prism has three pairs of rectangles with a total of 6 faces. Two rectangular faces have a length of 12 cm and a width of 6 cm, while the other two rectangles have a length of 12 cm and a width of 4 cm. The other pair of sides have a length of 6 cm and a width of 2 cm. We may also think that the surface area of the rectangular prism is the sum of the area of the six faces.
Let us now find the area of each rectangle.
| Given: length=12 cm width=6 cm Area of a Rectangle=l×w = (12 cm )( 6 cm ) =72 cm2 | Given: length=12 cm width=4 cm Area of a Rectangle=l×w =(12 cm )( 4 cm ) =48 cm2 | Given: length=6 cm width=4 cm Area of a Rectangle=l×w =( 6 cm )( 4 cm ) =24 cm2 |
Since the above computation only shows the area of a rectangle, we must double each to cover the area of their pair. Hence, we have,
Surface Area=2( 72 cm2 ) + 2( 48 cm2 ) + ( 2 24 cm2)
Surface Area=144 cm2+96 cm2 + 48 cm2
Surface Area=288 cm2
The total surface area of the top and bottom rectangles is 144 cm2. The total surface area of the front and back rectangles is 48 cm2, while the total surface area of the left and right rectangles is 48 cm2.
Thus, the rectangular pyramid has a total surface area of 288 cm2.
Now, let us try to use the formula for a rectangular prism’s surface area to solve this problem.
Here is the formula:
Surface Area (Rectangular Prism)=2 ( lw+wh+lh )
If we look at the given image as a 3D shape, we have its length = 12 cm, width = 6 cm, and height of 4 cm. Substituting the given values to the equation, we have,
Surface Area (Rectangular Prism)=2 ( lw+wh+lh )
Surface Area (Rectangular Prism)=2 [ ( 12×6 ) + ( 6×4 ) + ( 12×4 ) ]
Surface Area (Rectangular Prism)=2 (72+24+48)
Surface Area (Rectangular Prism)=2 ( 144 )
Surface Area Rectangular Prism=288cm2
Example 4
Determine the surface area of the net of a triangular prism illustrated below.
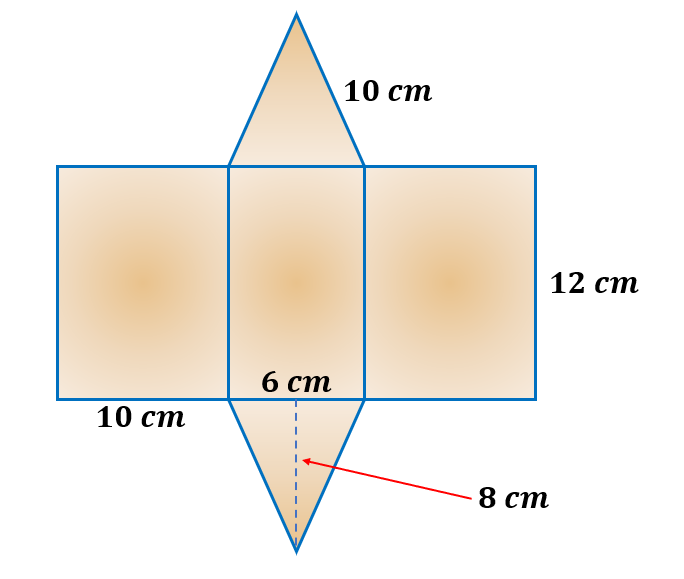
Solution:
The triangular prism above has 3 rectangles and 2 triangles on its sides. One of the rectangles is the base, while the other two have the same measure. To find the surface area of the geometric net, we must find the total of the areas of each shape.
To find the area of the base with a length of 12 cm and a width of 6 cm, we have,
Area ( Rectangle ) =l×w
Area ( Rectangle ) = 12 cm×6 cm
Area ( Rectangle ) =72 cm2
Hence, the rectangle’s area as the prism’s base is 72 cm2.
Here is how to find the area of the other two rectangles with a side length of 12 cm and a width of 10 cm.
Area ( Rectangle ) =l×w
Area ( Rectangle ) = 12 cm×10 cm
Area ( Rectangle ) =120 cm2
Thus, the two rectangles have a total area of 240 cm2 ( 120 cm2 2 ).
Finding the area of the triangle, we will use the formula, area( Triangle ) = ½ bh.
The base of the triangles measures 6 cm while the height is 8 cm.
Area( Triangle )=½ bh
Area( Triangle )=½ ( 6 cm )( 8 cm )
Area( Triangle )=½ ( 48 cm2 )
Area( Triangle )=$\frac{48}{2}$ cm2
Area( Triangle )=24 cm2
The total surface area of the two triangles is 48 cm2.
To find the total surface area of the triangle prism, we must all the areas of its faces.
Area ( Triangular Prism ) = 72 cm2+240 cm2+48 cm2
Area ( Triangular Prism ) = 360 cm2
Hence, the total surface area of the triangular prism is 360 cm2.
Example 5
Find the surface area of the cylinder.
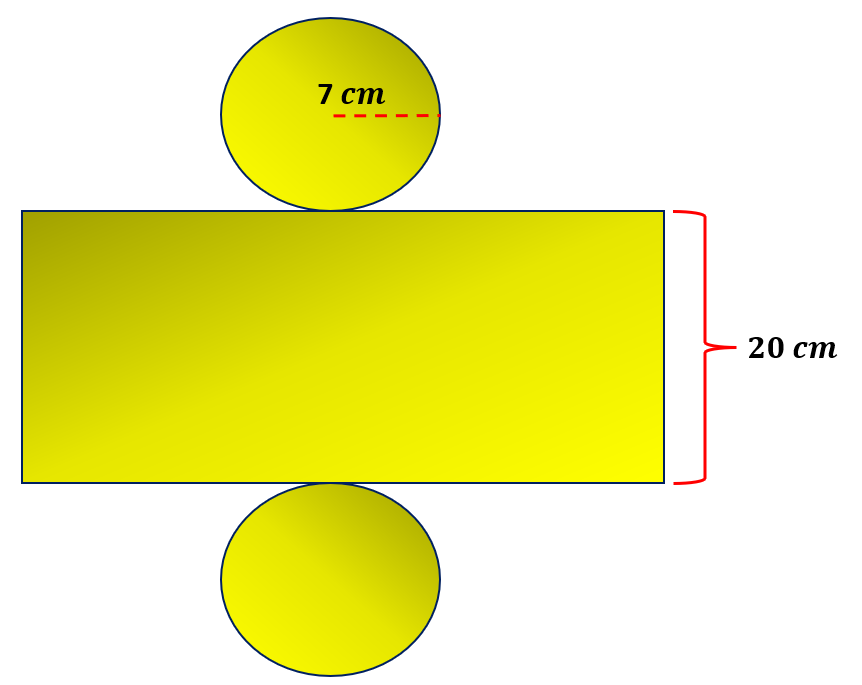
Solution:
A cylinder’s geometric net has a rectangle and two circles. The width of the rectangle, which is 20 cm, determines the cylinder’s height, and the rectangle’s length determines the circle’s circumference.
Here is the formula to find the area of the circle.
Area ( Circle ) = πr2
Since we have two circles, we have to double the value, that is,
Area (Circles) =2πr2
Area (Circles) =2π ( 7 cm )2
Area (Circles) =2π ( 49 cm2)
Area (Circles) =98π cm2
Let us find the circumference of the circle to solve for the length of the rectangle.
Circumference=2πr
Circumference=2π ( 7 cm )
Circumference=14π cm
We will use 14π cm as the length of the rectangle to find the area.
Area ( Rectangle )=l ×w
Area ( Rectangle )=14π cm×20 cm
Area ( Rectangle )=280π cm2
By adding the areas of the circles and the rectangle, let’s now determine the cylinder’s total surface area.
Area ( Cylinder )=Area ( Circles ) + Area ( Rectangle )
Area ( Cylinder )=98πcm2+280π cm2
Area ( Cylinder )=378π cm2
Thus, the surface area of the cylinder is 378π cm2 or approximately 1188 cm2.
How to use nets to find the volume
Example 1
Calculate the volume of the net of a cube below.
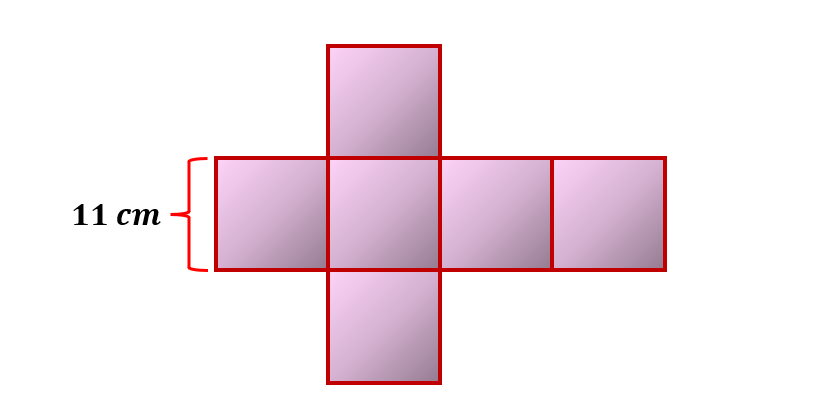
Solution:
Since we know that each side of the cube measures11 cm, it will be easy to solve for its volume by simply substituting it to the formula, Volume ( Cube ) = s3.
Hence, we have,
Volume ( Cube ) = ( 11 cm )3
Volume ( Cube ) =1331 cm3
Thus, the volume of the cube is 1331 cubic centimeters.
Example 2
Suppose that the image below shows a rectangular swimming pool for a house. Find the pool’s volume if it is 6 feet deep.
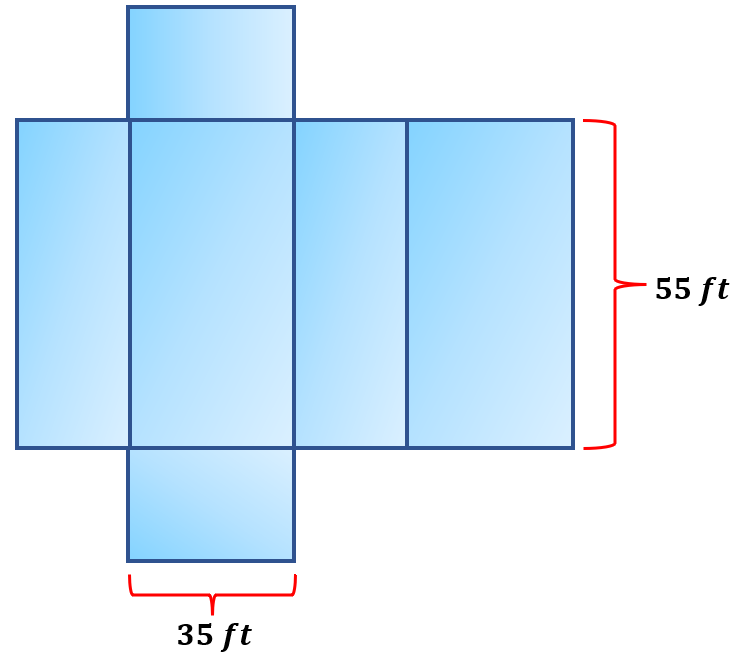
Solution:
The given figure can be seen as a rectangular prism with a length of 55 ft and a width of 35 ft. Since the pool is 6 feet deep, we will that value as its height. To get the volume of a rectangular prism, we use Volume ( Rectangular Prism ) = l×w×h.
Hence, we have,
Volume ( Rectangular Prism ) = 55 ft×35 ft×6 ft
Volume ( Rectangular Prism ) = 11550 ft3
Thus, the volume of the pool is 11550 ft3.
Example 3
Find the volume of the cylinder below, given its geometric net.
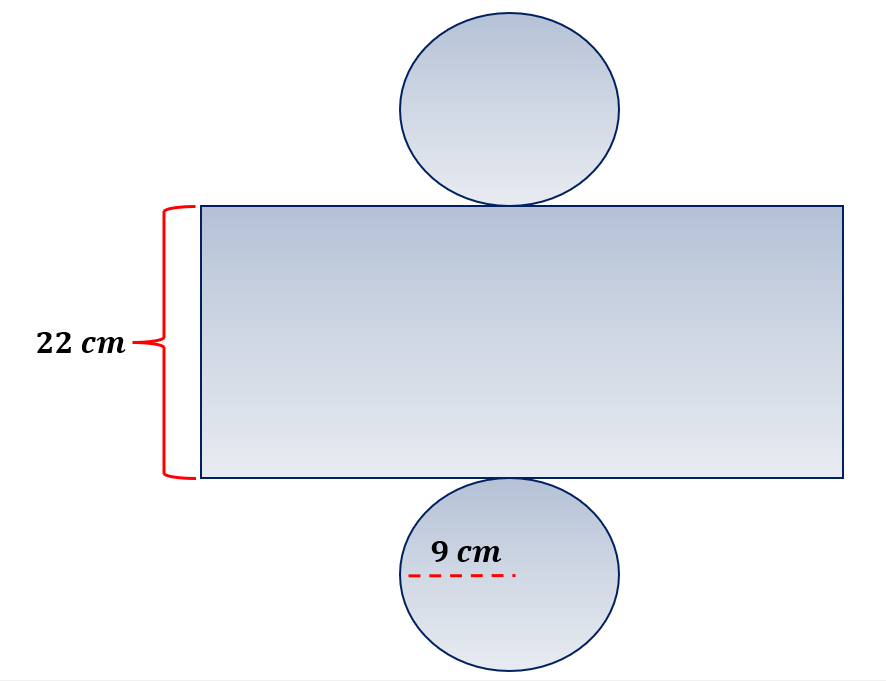
Solution:
The volume of a cylinder can be calculated using the formula,
Volume ( Cylinder ) = πr2h
The figure shows that the radius is 9 cm, and the height is 22 cm. Plugging in these measurements in the formula, we have,
Volume ( Cylinder ) =π ( 9 cm )2 ( 22 cm)
Volume ( Cylinder ) =π ( 81 cm2)( 22 cm )
Volume ( Cylinder ) =π ( 1782 cm3 )
Volume ( Cylinder ) =1782π cm3
Hence, the volume of the cylinder is 1782π cm3 or approximately 5598 cm3.
Example 4
A regular tetrahedron has a side length of 12 centimeters. Find its volume.
Solution:
A regular tetrahedron is a three-dimensional shape made up of four triangular faces. The formula that we may use to calculate its volume is:
Volume ( Tetrahedron ) = $\frac{a^3\sqrt{2}}{12}$
We will use 12 cm as the side length of the given tetrahedron and substitute it for the variable a in the formula. Hence,
Volume ( Tetrahedron ) = $\frac{12^3\sqrt{2}}{12}$
Volume ( Tetrahedron ) =( 122) √2
Volume ( Tetrahedron ) =144√2cm3
Thus, the volume of the tetrahedron is 144√2cm3 or approximately 204 cubic centimeters.
Summary
A geometric net refers to a two-dimensional shape that can be modified to create a solid or a three-dimensional shape.
These are the conditions to be met if a net forms a solid or a three-dimensional shape:
( 1 ) Make sure that both the solid and the net have the same number of faces and that the solid’s faces correspond to the same faces in the net in terms of shape.
( 2 ) Make sure that all the sides fit together properly by picturing how the net will be folded to create the solid.
There are characteristics shared by all three-dimensional shapes: face, edge, and vertex.
The surface area is the area or region that an object’s surface occupies
The volume refers to how much space an object has.
Frequently Asked Questions on Geometric Nets (FAQs)
What is meant by geometric net?
A geometric net refers to a two-dimensional shape that can be modified to create a solid or a three-dimensional shape. These are some examples of geometric nets:
Net of a Cube | Net of a Triangular Prism | Net of a Rectangular Prism |
Net of a Square-based Prism | Net of a Tetrahedron | Net of a Cylinder |
How are geometric nets formed?
Geometric nets are formed using two-dimensional shapes. The table below shows the list of geometric nets and the shapes used to form them.
| Geometric Nets | Shapes Used |
| Cube | Six squares |
| Rectangular Prism | Six rectangles |
| Triangular Prism | 2 Rectangles and 2 Triangles |
| Square-based Prism | 1 Square and 4 Triangles |
| Triangular-based Prism | 4 Triangles |
| Cylinder | 1 Rectangle and 2 Circles |
| Hexagonal Pyramid | 1 Hexagon and 6 Triangles |
| Hexagonal Prism | 2 Hexagon and 6 Rectangles |
| Octahedron | 8 Triangles |
| Dodecahedron | 12 Pentagons |
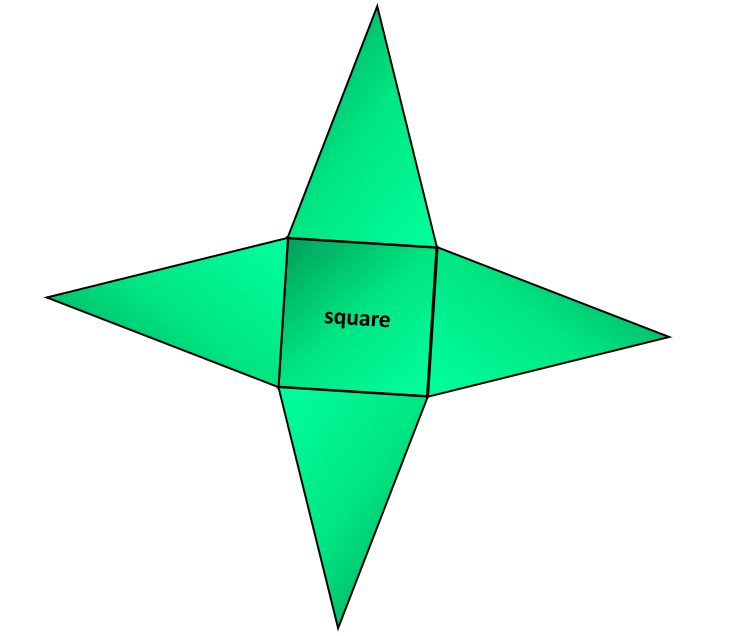
How to draw a square-based pyramid?
A square-based pyramid has a base that is square and faces that are triangular and meet at a vertex above the base. To draw the net of a square-based pyramid, here are the steps:
( 1 ) Draw a square. Keep in mind that every side of a square is the same length. This square is the base of the pyramid.
( 2 ) On each side of the square, draw an isosceles triangle. An isosceles triangle is a triangle having two sides of equal length.
The example is shown below.
What does the net of a hexagonal pyramid look like?
A hexagonal pyramid is a pyramid that has a hexagonal base and six isosceles triangles that meet at a common vertex. The image below shows the net of a hexagonal pyramid.

A hexagonal pyramid has seven ( 7 ) faces twelve ( 12 ) edges, and seven ( 7 ) vertices.
Why is it important to learn geometric nets?
A geometric net is a two-dimensional shape that can be modified to create a solid or a three-dimensional shape. Students who study geometric nets can relate to and connect given 2D dimensional shapes and form three-dimensional shapes. In the process of problem-solving and developing higher-order cognitive abilities, a spatial understanding is also thought to be essential.
Understanding how a three-dimensional shape is constructed from two-dimensional parts is important for every aspect of three-dimensional design, not just when building boxes. Engineers and developers use powerful and advanced computer-aided design (CAD) software to assist in their work. The vital spatial skills you acquire from a foundational understanding of form nets can thus develop further into other more challenging design applications.
We may typically identify two measurements if we know geometry nets of three-dimensional shapes: volume and surface area.
For the volume, let us say, for instance, the amount of water a particular solid figure contains. For the surface area, for example, how much paint would need to be applied to cover the shape’s outside entirely?
What is the distinction between volume and surface area?
The area or region that an object’s surface occupies is known as its surface area. Contrarily, the volume describes how much space an object occupies.
What is a cuboid’s geometric net?
A cuboid is a rectangular prism with eight vertices, twelve edges, and six rectangular faces. Every corner of a cuboid is at a 90-degree angle.
Recommended Worksheets
Geometric Nets (National Inventors’ Day Themed) Math Worksheets
Kinds of Shapes (Christmas Themed) Math Worksheets
Lateral Surface Area (St. Patrick’s Day themed) Math Worksheets









