Area of a Rectangle
A rectangle is a type of quadrilateral that is similar to a square in the fact that it has that equal opposite sides and four right angles. But, unlike square where the length and the breadth are the same, in rectangle, we have different dimensions of length and breadth.
Here we have a rectangle, covered with small squares. Each small square stands for 1 square centimetre, that is, each small square is cm on each side.
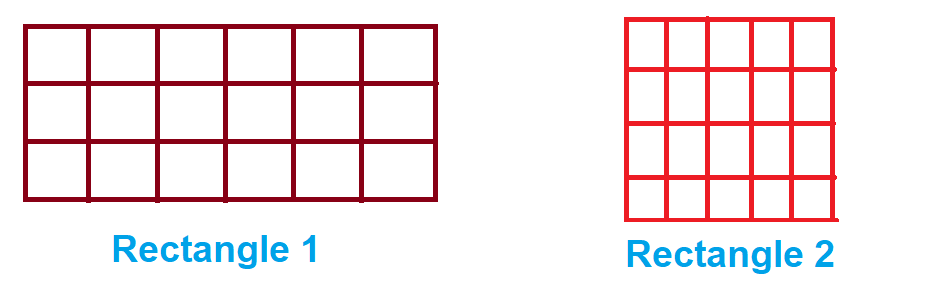
Count the number of squares that cover each rectangle. This will give you the area of a rectangle in square centimetres. Also, write the length and breadth of each rectangle. What do you observe? Let’s find out.
Rectangle 1
Number of small squares = 18
Area = 18 cm2 or 18 sq. cm
Length = 6 cm
Breadth = 3 cm
Rectangle 2
Number of small squares = 20
Area = 20 cm2 or 20 sq. cm
Length = 5 cm
Breadth = 4 cm
From the above examples, you can see that there is a quicker way to find the area in each case without having to count the number of squares. Since 6 x 3 = 18 and 5 x 4 = 50, we can say that the area of each of the two rectangles can be found out by multiplying the measures of length and breadth of the rectangle.
Area of a rectangle having length ‘l’ and breadth ‘b’ is given by l x b
For example, let us consider a rectangle having a length of 8 cm and a breadth of 7 cm as shown in the figure below.
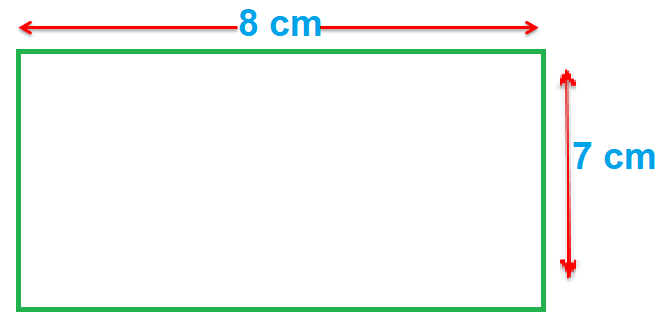
The area of this rectangle is given by 8 7 7 = 56 cm2.
Hence
Area of a rectangle = length x breadth
How to calculate the length and breadth of a rectangle using its area?
We now know how to calculate the area if we have the length and the breadth of a rectangle. But, if only the length or breadth and area are given, is it possible to know the breadth of the rectangle? Let us find out.
Since, Area of a rectangle = Length x Breadth,
Therefore,
Length = Area / Breadth, Breadth = Area / Length
Solved Examples
Example 1
Find the height of the wall whose length is 4m and which can be covered by 2400 tiles of size 25 cm by 20 cm.
Solution
Area of tiles = (25 x 20) cm2 = 500 cm2
Therefore, area of 2400 tiles = 2400 x 500 cm2
= 1200000 cm2
= 1200000 / 10000 m2 (10000 cm2 = 1 m2)
= 120 m2
Let the height of the wall be “h” metres. Then,
Area of the wall = 4 x h m2 = 4h m2
Since 2400 tiles completely cover the wall, therefore,
Area of the wall = Area of 2400 tiles
⇒ 4h = 120
⇒ h = = 30
Hence, height of the wall is 30 metres.
Example 2
Find the area, in square metres, of a rectangle whose
a) length = 4.5 m and breadth = 1.6 m.
b) length = 3 dm 6 cm, breadth = 2 dm 9 cm
Solution
a) We have,
Length = 4.5 m and Breadth = 1.6 m
Area of the rectangle = Length x Breadth
Hence, Area of the rectangle = (4.5 x 1.6) m2 = 7.20 m2
b) We have,
Length = 3 dm 6 cm = (3 x 10 + 6) cm = 36 cm = 0.36 m (∵ 1 dm = 10 cm)
Breadth = 2 dm 9 cm = (2 x 10 + 9) cm = 29 cm = 0.29 m
Area of the rectangle = Length x Breadth
Hence, Area of the rectangle = (0.36 x 0.29) m2 = 0.1044 m2
Example 3
A grassy plot is 80 m x60 m. Two cross paths each 4 m wide are constructed at right angles through the centre of the field, such that each path is parallel to one of the sides of the rectangles. Find the total area used path. Also, find the cost of gravelling them at £ 5 per square metre.
Solution
An important strategy for solving such questions is to first visualise them. Therefore, we will construct the rectangle and plot the details we have been given in the question.
Let the ABDC and PQSR be the rectangular paths that are to be constructed at right angles through the centre of the field, such that each path is parallel to one of the sides of the rectangles. We have,
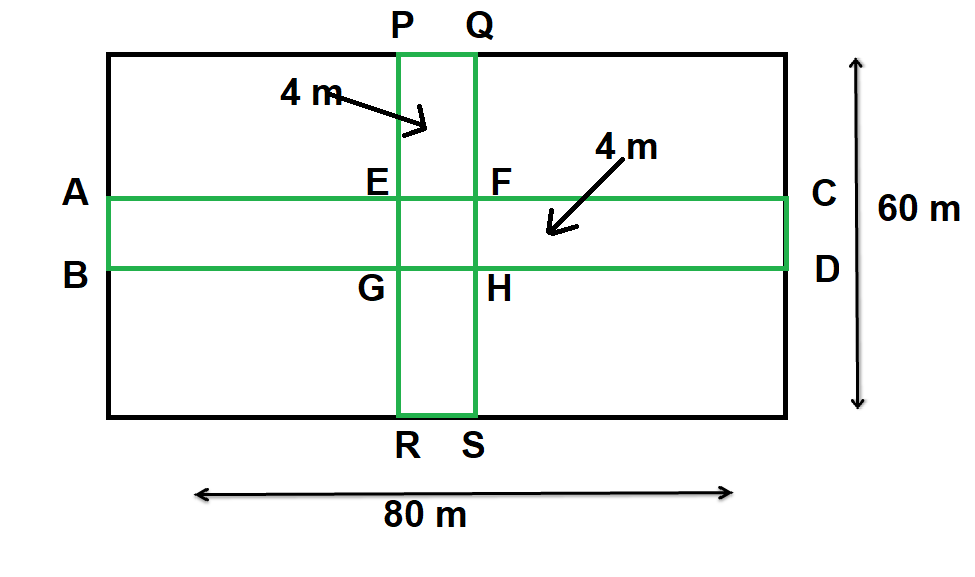
We have to find the total area used path.
First, we will calculate the area of the path ABDC.
Since the grassy plot is a rectangle and we know that area of a rectangle having length ‘l’ and breadth ‘b’ is given by l x b, therefore,
Area of the path ABDC =(80 x 4) m2 = 320 m2
Again, let us now find out the area of the path PQSR which can be calculated in the same manner as done above.
We have,
Area of the path PQSR = (60 x 4) m2 = 240 m2
But, with the help of our figure, we can clearly see that the area of EFHG is common to both the areas that we have calculated just now. Hence we need to subtract this area once from our result to avoid counting it twice.
Area of the path EFHG = (4 x 4) m2 = 16 m2
Therefore,
Total area of the path = Area of the path ABDC + Area of the path PQSR – Area of the path EFHG
Hence,
Total area of the path = (320 + 240 – 16 ) m2 = 544 m2
Now, let us cost for gravelling the path.
We have been given that the cost of gravelling the path is £5 per square metre.
Since the total area to be gravelled is 544 m2, therefore,
The total cost of gravelling the path would be £ (544 x 5) = £2720.
Example 4
A rectangular path is 45 m long and 30 m wide. A path 2.5 m wide is constructed outside the park. Find the area of the path.
Solution
Let ABCD be the rectangular path and the shaded region represents the 2.5 m wide path to be constructed outside the park.
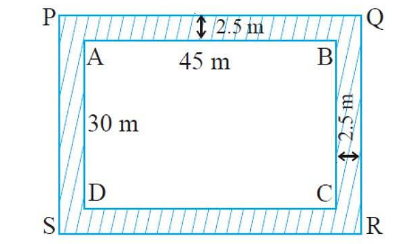
We have,
PQ = (45 +2.5 + 2.5) m = 50 m
PS = (30 + 2.5 + 2.5) m = 35 m
Area of rectangle PQRS = (50 x 35) m2 = 1750 m2
Area of rectangle ABCD = (45 x 30) m2 = 1350 m2
Clearly,
Area of the path = Area of rectangle PQRS – Area of rectangle ABCD
= 1750 m2 – 1350 m2
= 400 m2
Hence, area of the path = 400 m2
Example 5
Find the length of a rectangle, if its area = 90cm2 and breadth = 6 cm
Solution
We are given that area = 90cm2 and breadth = 10 cm
Now, Length = Area/Breadth
Hence, Length = 90/6 cm = 15 cm
Therefore, the length of the rectangle having area = 90cm2 and breadth = 6 cm is 15 cm
Example 6
A gallery 1.25 m wide is constructed all along the outside of a room 5.5 m long and 4 m wide. Find
a) The area of the gallery
b) The cost of cementing the floor of the gallery at the rate of £20 per m2
Solution
a) Let us first mark and understand the given information through a diagrammatic representation. Let ABCD represent the floor of the room and the shaded region represent the floor of the 1.25 m wide gallery.

We have
PQ = (5.5 + 1.25 + 1.25) m = 8 m and
PS = (4 + 1.25 + 1.25) m = 6.5 m
Now,
Area of the rectangle PQRS = PQ x PS
= 8 x 6.5 m2
= 52 m2
Area of the rectangle ABCD = AB x AD
= (5.5 x 4) m2
= 22 m2
Now,
Area of the gallery = Area of the rectangle PQRS – Area of the rectangle ABCD
= (52 – 22) m2 = 30 m2
Hence, area of the gallery = 30 m2
b) Now that we have calculated the area of the gallery, we need to find out the cost of cementing of the gallery.
We have been given that,
Rate of cementing the floor of the gallery = £20 per m2
Therefore,
Cost of cementing the floor of the gallery = £(20 x 30) = £600
Hence, the cost of cementing the floor of the gallery = £600
Example 7
A room is 7 m long and 5.5 m broad. It has one door of length 2 m and breadth 1.5 m and two windows each of length 1.5 m and breadth 1 m. Find
a) Area of the door
b) Area of the windows
c) Area of the four walls
d) Cost of whitewashing the walls at the rate of £50 per square metre if the walls are 3.5 m high.
Solution
a) Let us first understand what information has been provided in the question. We have been given that
Length of the door = 2 m
Breadth of the door = 1.5 m
Area of the door = (2 x 1.5) m2 = 3 m2
Hence, area of the door = 3 m2
Similarly, we can calculate the area of the windows.
b) We have been given that
Length of one window = 1.5 m
Breadth of one window = 1 m
Area of one window = (1.5 x 1) m2 = 1.5 m2
Area of two windows = 1.5 x 2 = 3 m2
Hence, area of two windows = 3 m2
c) Now, let us calculate the area of the four walls. We have been given that
Length of the room = 7 m
Breadth of the room = 5.5 m
Height of the room = 3.5 m
Area of the four walls = (Length x Height) + (Length x Height) + (Breadth x Height) + (Breadth x Height)
Therefore,
Area of the four walls = 2 (Length x Height) + 2(Breadth x Height)
Using distributive property over addition, we have
Area of the four walls = 2 ((Length + Breadth) x Height
= [2 (7 + 5.5) x 3.5] m2
= [2 x 1.5 x 3.5] m2
= 87.5 m2
Hence, area of the four walls = 87.5 m2
d) Now, let us the cost of whitewashing the walls. We have been given that the Cost of whitewashing the walls is at the rate of £50 per square metre.
So,
Cost of whitewashing 1 m2 = £50
Cost of whitewashing 87.5 m2 = £ (50 x 81.5) = £4075
Hence Cost of whitewashing = £4075
Example 8
A rectangular garden and a square garden have the same perimeter of 100 m. If the rectangular garden has a breadth 2 m less than that of the square garden, find
a) the breadth of the rectangular garden
b) the length of the rectangular garden
c) the area of the rectangular garden
Solution
We have been given that the rectangular garden and the square garden have the same perimeter. We know that all sides of a square are equal and the perimeter of a square = 4 x Side.
Therefore, we can say that
4 x Side = 100 m
Side = 100/4 = 25 m
Hence, the side of the square = 25 m.
We have also been given that the rectangular garden has a breadth 2 cm less than that of the square garden. This means that the breadth of the rectangular garden = 25 – 2 = 23 m.
Hence, breadth of the rectangular garden = 23 m
b) Now, we need to find the length of the rectangular garden. We now know the breadth of the rectangular garden and its perimeter, since the rectangular garden and the square garden have the same perimeter. We also know that
Perimeter of a rectangle = 2 (Length + Breadth)
Therefore,
2 (Length + 23) = 100 m
2 x Length + 46 = 100 m
2 x Length = (100 – 46) m
2 x Length = 54 m
Length = 54/2 m = 27 m
Hence, length of the rectangular garden = 27 m
c) Next, we need to find the area of the rectangular garden. From the previous calculations, we have both the length and the breadth of the rectangular garden, i.e.
Length of the rectangular garden = 27 m
Breadth of the rectangular garden = 23 m
We know that,
Area of the rectangle = Length x Breadth
Therefore,
Area of the rectangular garden = (27 x 23) m2
= 621 m2
Area of the rectangular garden = 621 m2
Example 9
A magazine charges £300 per 10 sq. cm area for advertising. A company decided to order a half-page advertisement. If each page of the magazine is 15 cm x 24 cm, what amount will the company pay for the advertisement?
Solution
We have been given that the dimensions of each page of the magazine are 15 cm x 24 cm. This means that the magazine is rectangular in shape. We take the larger side of the magazine as the length and the shorter one as the breadth. We have,
Length of one page of the magazine = 24 cm
Breadth of one page of the magazine = 15 cm
We know that,
Area of the rectangle = Length x Breadth
Therefore,
Area of one page of the magazine = (24 x 15) cm2 = 360 cm2
Area of half-page of the magazine = 1/2 x 360 cm2 = 180 cm2
Now charges for 10 sq. cm advertisement = £300
Therefore, charges for 1 sq. cm advertisement = £300/100 = £30
Now,
Charges for half page of the advertisement = Area of half page of the magazine x Charges for 10 sq. cm advertisement
Hence,
Charges for half page of the advertisement = £ (180 x 30) = £ 5400
Therefore, the company has to pay £5400 for a half-page advertisement
Example 10
State True or False for the following statement and give reasons for your answer.
Statement – “If the length of a rectangle is halved and the breadth is doubled, then the area of the rectangle obtained remains the same”
Solution
Let there be a rectangle having the length “l” and breadth “b”. Now we know that
Area of the rectangle = Length x Breadth = l x b ………………………………………….. (1)
Now we have been given that the length of the new rectangle is halved.
Therefore, the length of the rectangle now becomes l/2
Also, the breadth of the rectangle is doubled. This means that the breadth of the rectangle now becomes 2b.
The area of the rectangle will now be = l/2 x 2b = l x b……………………………………..(2)
Since both the formulas obtained for calculating the areas in (1) and (2) are the same, this means that the statement “If the length of a rectangle is halved and the breadth is doubled, then the area of the rectangle obtained remains the same” is True.
Recommended Worksheets
Area of Squares and Rectangles (Real Estates Themed) Worksheets
Solving Word Problems Involving Perimeter and Area of Rectangle 4th Grade Math Worksheets
Shape Partitions (Rectangles and Circles) 2nd Grade Math Worksheets









