Introduction
Mathematics requires abilities in observation and categorization. Students must concentrate on the distinct qualities to learn the differences between shapes. Students gain the ability to recognize various shapes through the application of observational skills. They also learn how to compare multiple shapes and organize similar ones together. Students can recognize numbers and how they appear better if they strongly understand shapes. The students have an advantage in several learning areas because they are familiar with shapes.
This article will define regular and irregular shapes, discuss how they differ and provide some examples.
What does a regular shape mean?
Definition
A regular shape is a two-dimensional (2D) shape whose (interior) angles and sides all have the same measurements.
What are examples of regular shapes?
The following are some examples of regular shapes and their basic properties.

Equilateral Triangle
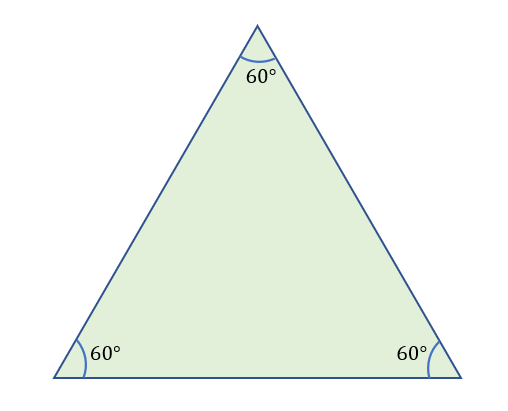
An equilateral triangle has three (3) equal sides and three (3) equal interior angles. A regular triangle’s inner angles add up to 180 degrees, with each angle measuring 60 degrees.
The illustration below shows an equilateral triangle with three sides of equal length and 60-degree interior angles.
Square
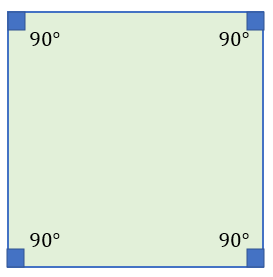
A square has four (4) equal sides and four (4) equal angles. In a square, each inside angle is 90 degrees.
The shape of the square below shows that each side has the same length and that each inner angle creates a 90-degree angle.
Regular Pentagon
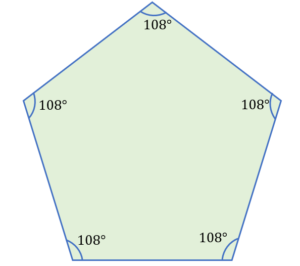
Five equal sides and five equal angles make up a regular pentagon. A regular polygon’s interior angles are each 108 degrees in measure. The sum of all the interior angles is 540 degrees.
The regular pentagon below has a shape that illustrates that each side has the same size and that each interior angle is 108 degrees.
Regular Hexagon
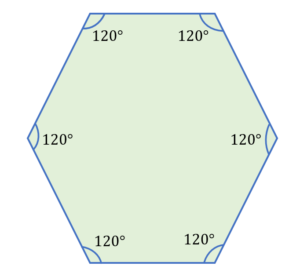
A regular hexagon has six (6) equal sides and six (6) equal angles. In a regular hexagon, each interior angle measures 120 degrees; hence the total number of interior angles is 720 degrees.
The regular hexagon shown below has six equal sides and internal angles that are each 120 degrees.
Regular Heptagon
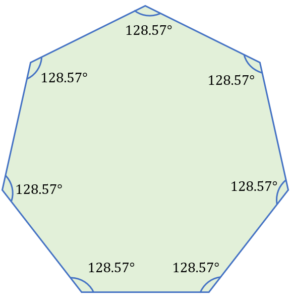
A regular heptagon has seven (7) equal sides and seven (7) equal angles. A regular heptagon’s internal angles add up to 900 degrees in total.
The regular heptagon below shows its properties of having seven sides of equal lengths, and each of its interior angles measures 128.57.
Regular Octagon
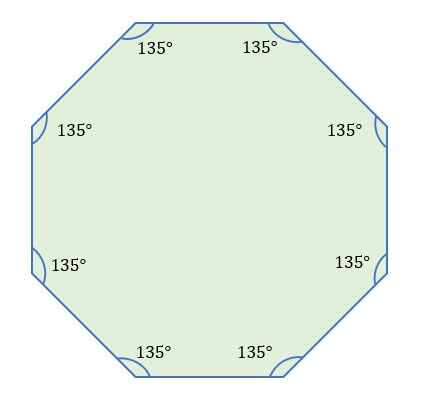
A regular octagon has eight (8) equal sides and eight (8) equal angles. A regular octagon’s interior angles add up to 1080 degrees or 135 degrees for each interior angle.
A regular octagon with eight equal sides and internal angles that are each 135 degrees is shown below.
Regular Decagon
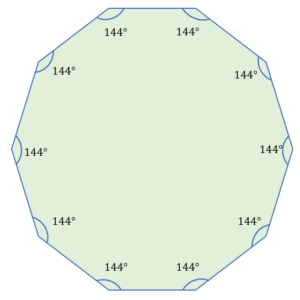
A regular decagon has ten (10) equal sides and ten (10) equal angles. Each interior angle in a regular decagon measures 144 degrees and adds up to 1440 degrees.
Below is an illustration of a regular decagon with equal-length sides and 144-degree interior angles.
Regular Dodecagon
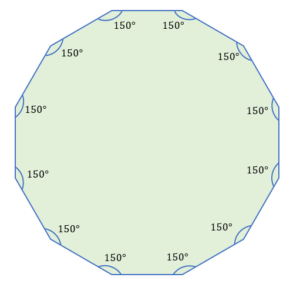
Twelve equal sides and twelve equal angles make up a regular dodecagon. Regular dodecagons have interior angles total up to 1800 degrees, each measuring 150 degrees.
The normal dodecagon shown below has equal-length sides and internal angles that are 150 degrees.
Sum of the Interior Angles of Regular Shapes
Interior angles are the angles created when line segments are joined end to end inside the polygon at its corners. The total measurement of all the interior angles added together within the polygon is known as the sum of the interior angles. We divide a regular polygon into triangles to calculate the sum of its internal angles. We may calculate the sum of interior angles in a regular polygon by multiplying the number of triangles in the polygon by 180° because the sum of interior angles in a triangle is 180°.
As illustrated below, a regular pentagon can be divided into three triangles using its diagonals, a regular hexagon can have four, and a regular octagon can have six triangles.

We use the following formula to find the sum of the interior angles of a regular polygon:
Sum of the interior angles=( n-2 )×180°
where n is the number of sides.
For example, let us get the sum of the interior angles of a regular hexagon, a regular pentagon, and a regular octagon.
Sum of Interior Angles of a Regular Pentagon
We shall use n=5 because a regular pentagon has five equal sides. Hence, we have,
Sum of the interior angles= ( 5-2 ) ×180°
Sum of the interior angles= 3×180°
Sum of the interior angles= 540°
As a result, a regular pentagon’s internal angles add up to 540 degrees.
Sum of Interior Angles of a Regular Hexagon
A regular hexagon has six equal sides, so we will use n=6. Thus, we have,
Sum of the interior angles= ( 6-2 ) ×180°
Sum of the interior angles= 4×180°
Sum of the interior angles= 720°
Consequently, a regular hexagon’s interior angles add up to 720 degrees.
Sum of Interior Angles of a Regular Heptagon
Since a regular heptagon has seven equal sides, we will use n=7. Hence, we have,
Sum of the interior angles= ( 7-2 ) ×180°
Sum of the interior angles= 5×180°
Sum of the interior angles= 900°
Thus, a regular heptagon’s interior angles add up to 900 degrees.
Sum of Interior Angles of a Regular Octagon
Since a regular octagon has eight equal sides, we will use n=8. We have,
Sum of the interior angles= ( 8-2 )×180°
Sum of the interior angles=6×180°
Sum of the interior angles=1080°
Therefore, the total interior angle of a regular octagon is 1080 degrees.
Sum of interior angles of a Regular Decagon
Since a regular decagon has ten (10) equal sides, we will use n=10. We have,
Sum of the interior angles= ( 10-2 )×180°
Sum of the interior angles= 8×180°
Sum of the interior angles= 1440°
As a result, a regular decagon’s interior angles total 1440 degrees.
The Sum of a Regular Dodecagon’s Interior Angles
Since a regular decagon has twelve (12) equal sides, then we will use n=12. We have,
Sum of the interior angles= ( 12-2 ) ×180°
Sum of the interior angles= 10×180°
Sum of the interior angles= 1800°
Therefore, the total internal angle of a standard dodecagon is 1800 degrees.
The measurements of each interior angle and their sum are displayed in the table below for a few regular shapes or regular polygons.
| Regular Shape | Sides | The Measure of Each Interior Angle | Sum of the Interior Angles |
| Equilateral Triangle | 3 | 60 degrees | 180 degrees |
| Square | 4 | 90 degrees | 360 degrees |
| Pentagon | 5 | 108 degrees | 540 degrees |
| Hexagon | 6 | 120 degrees | 720 degrees |
| Heptagon | 7 | 128.57 degrees | 900 degrees |
| Octagon | 8 | 135 degrees | 1080 degrees |
| Decagon | 10 | 144 degrees | 1440 degrees |
| Dodecagon | 12 | 150 degrees | 1800 degrees |
The Perimeter of Regular Shapes
The perimeter of a regular shape is the total distance around its edge. Finding the perimeter of regular shapes is adding all the side lengths. Another way is to multiply the given side length by the number of sides of the regular shape.
As an illustration, suppose we need to determine the perimeter of an equilateral triangle with a length of 5 cm. All three of the triangle’s sides are 5 cm long since an equilateral triangle is a regular shape. To find its perimeter, we have,
Perimeter=5 cm+5 cm+5 cm
Perimeter=15 cm
Alternative solution:
Perimeter=3 ( 5 cm )
Perimeter= 15 cm
Hence, the equilateral triangle’s perimeter with a 5 cm side length is 15 cm.
Let us take the regular shape below as an example and say we wish to determine its perimeter.
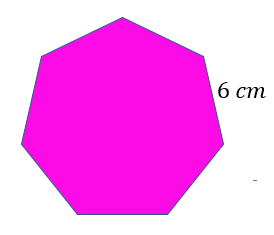
The shape is a regular pentagon since it has seven sides with equal measurements. Since we already know that one side is 6 cm, it is easy to calculate its perimeter. Hence, we have,
Perimeter=6 cm + 6 cm + 6cm + 6 cm + 6 cm + 6 cm + 6 cm
Perimeter=42 cm
Alternative solution:
Perimeter=7 ( 6 cm )
Perimeter= 42 cm
Thus, the perimeter of the regular pentagon with a side length of 6 cm is equal to 42 cm.
What does an irregular shape mean?
Definition
An irregular shape is a shape with sides and angles of any length and measurement. An irregular shape’s number of straight sides is sometimes used to decide its name. A shape is irregular, even if only one side has a different measurement. There are irregular shapes that belong to the quadrilateral family with distinctive names, including the parallelogram, rhombus, and kite.
What are examples of irregular shapes?
Irregular shapes have varying lengths and measurements. Thus, the following are some examples of irregular shapes.
Isosceles Triangle
An isosceles triangle is a shape having two equal-length sides. Only two sides in the illustration below have the same measurement, indicating that this is an irregular shape.
Scalene Triangle
Triangles with different-sized sides are called scalene triangles. A scalene triangle with various side lengths and interior angles is shown in the image below.
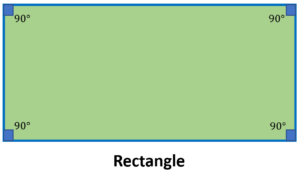
Rectangle
A rectangle has four sides forming two pairs of parallel sides of equal lengths. Each interior angle in a rectangle measures 90 degrees. The rectangle below shows that two opposite sides have the same measurement, and each interior angle measures 90 degrees.
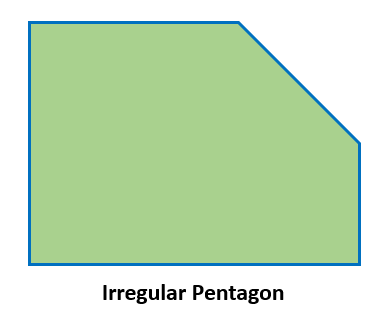
Irregular Pentagon
A shape with five unequal sides is referred to as an irregular pentagon. Even if not all the sides of an irregular pentagon are equal in length, it is possible for two or three of them to be. The image below shows an irregular pentagon with five unequal side lengths.
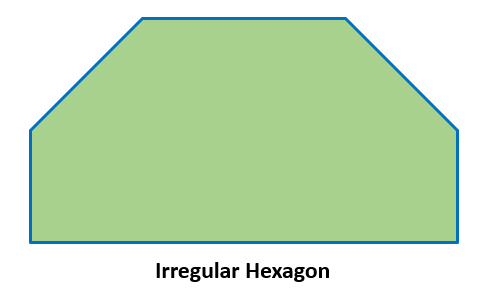
Irregular Hexagon
An irregular hexagon has six sides and six angles of different measurements. Below is an example of an irregular hexagon.
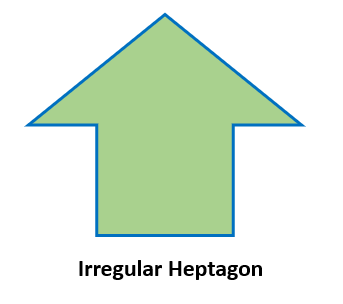
Irregular Heptagon
An irregular heptagon is a shape with different measurements of seven sides and seven angles. The image below is an example of an irregular heptagon.
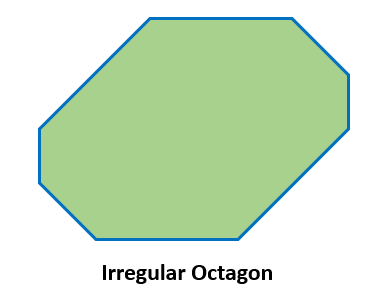
Irregular Octagon
An irregular octagon is a shape with eight sides and eight angles of varying measurements. An example of an irregular octagon is shown below.
Irregular Decagon
An irregular decagon is a shape with ten sides and ten angles of different measurements. Here is an example of an irregular decagon.

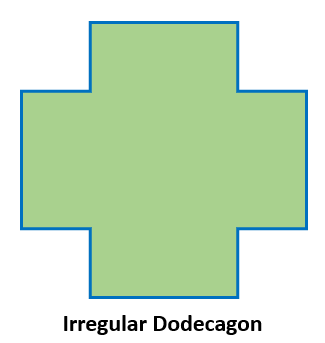
Irregular Dodecagon
A shape with twelve sides and twelve angles of various measurements is known as an irregular dodecagon. Here is an illustration of an irregular dodecagon.
The Perimeter of Irregular Shapes
The distance of the boundary of the irregular shape is its perimeter. Simply put, an irregular shape’s perimeter equals the total of all its sides.
Let us say, for example, we have the following irregular shapes, and we want to find the perimeter.
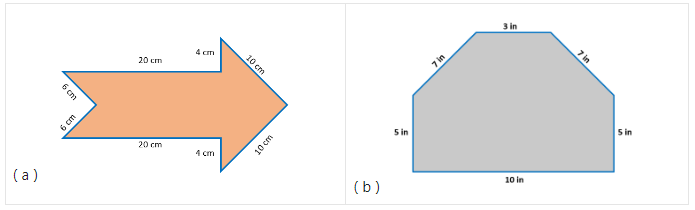
Solution:
( a ) The figure is an irregular octagon since it has eight sides with different measurements. To find its perimeter, we must add the lengths of its eight sides.
Perimeter= 20 cm + 20 cm + 10 cm + 10 cm + 6 cm + 6 cm + 4 cm + 4 cm
Perimeter= 80 cm
Hence, the perimeter of the given irregular octagon is 80 centimetres.
( b ) Since the given figure has six sides with varying lengths, it is an irregular hexagon. To find its perimeter, we have,
Perimeter= 10 in + 7 in +7 in + 5 cin + 5 in +3 in
Perimeter= 37 in
Therefore, the perimeter of the irregular hexagon is 37 inches.
Difference Between Regular and Regular Shapes
It is important to check the sides and angles to differentiate between regular and irregular shapes. If the given shape has the same lengths of sides and angle measurement, it is a regular shape. If the given shape has different lengths of sides and angles measurement, then it is an irregular shape. Some examples of regular and irregular shapes, together with their properties, are shown in the table below.
| Regular Shapes | Irregular Shapes |
Equilateral Triangle The interior angles and all three sides are equal. | Isosceles Triangle Only two sides are of equal lengths. |
Square All four sides and interior angles are equal. | Rectangle Only the opposite sides have equal measurements. |
Pentagon All five sides and interior angles are equal. | Irregular Pentagon The five sides have different lengths. |
Hexagon All six sides and interior angles are equal. | Irregular Hexagon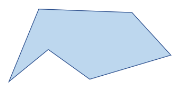 The six sides have varying measurements. |
Heptagon All seven sides and interior angles are equal. | Irregular Heptagon The seven sides have different lengths. |
Octagon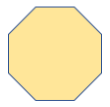 All eight sides and interior angles are equal. | Irregular Octagon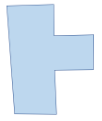 It has eight sides with different lengths. |
Decagon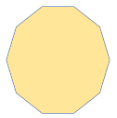 All ten sides and interior angles are equal. | Irregular Decagon It has ten sides of varying measurements. |
Dodecagon All twelve sides and interior angles are equal. | Irregular Dodecagon It has twelve sides of unequal lengths. |
More Examples
Example 1
Determine whether the shape in the illustration is regular or irregular.

Answers:
( a ) The figure shows a regular shape. Since it has five sides with equal lengths and corners with the same angle measurements, it is a regular pentagon.
( b ) The shape is irregular since its sides have varying lengths. Since it has eight sides, then it is an irregular polygon.
( c ) The shape is regular since it has sides of equal lengths and angles. Since it has eight sides and eight corners, it is a regular octagon.
( d ) It is an irregular shape since it has sides of different lengths. Since the shape has six uneven sides, it is an irregular hexagon.
( e ) The shape is irregular with twelve unequal side lengths. Thus, it is an irregular dodecagon.
Example 2
Name the following regular shapes.
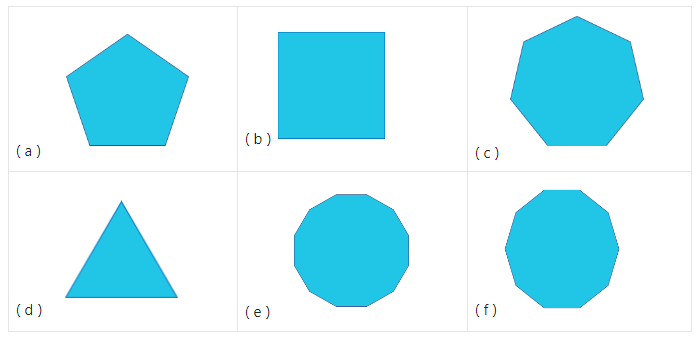
Answers:
( a ) Regular pentagon
( b ) Square
( c ) Regular heptagon
( d ) Equilateral triangle
( e ) Regular dodecagon
( f ) Regular decagon
Example 3
Calculate the perimeter of each shape.

Solution:
( a ) The regular shape is a square since it has four equal sides and angles. Since one side length is given already, we have,
Perimeter ( square )= 5 cm +5 cm +5 cm +5 cm
Perimeter ( square ) = 20 cm
We can also multiply 5 cm by 4 since a square has four sides.
Perimeter=4 ( 5 cm )
Perimeter=20 cm
Therefore, the perimeter of the square is 20 centimetres.
( b ) The shape is an irregular pentagon. As shown in the image, the five sides of the given shape do not have the same lengths. To calculate its perimeter, we have,
Perimeter=6 cm+4 cm+4 cm+2 cm+2 cm
Perimeter=18 cm
Thus, the perimeter of the irregular pentagon is 18 centimetres.
( c ) The given shape is a regular decagon because it has ten (10) equal side lengths and ten (10) angles. It is enough to know the length of one side to find its perimeter. Since the given side length is 3 inches, we must multiply it by 10, which is the number of sides of a decagon. Here is the math,
Perimeter=10 ( 3 in )
Perimeter=30 in
We can also do repeated addition, so we have,
Perimeter=3 in+3 in+3 in+3 in+3 in+3 in+3 in+3 in+3 in+3 in
Perimeter=30 in
Therefore, the regular decagon’s perimeter is 30 inches.
( d ) The shape is an irregular octagon since it has eight uneven side lengths. To find its perimeter, let us add the given measurements of each side. We have,
Perimeter=13 in + 6 in + 6 in + 5 in + 5 in + 3 in + 3 in + 3 in
Perimeter=44 in
Thus, the perimeter of the irregular decagon is 44 inches.
Summary
A regular shape is a two-dimensional (2D) shape whose (interior) angles and sides all have the same measurements.
Equilateral triangles, squares, regular pentagons, regular hexagons, regular heptagons, regular octagons, regular decagons, and regular dodecagons are a few examples of regular shapes.
An irregular shape is a shape with sides and angles of any length and measurement.
Isosceles triangles, scalene triangles, irregular pentagons, irregular hexagons, irregular heptagons, irregular octagons, irregular decagons, and irregular dodecagons are a few examples of irregular shapes.
Frequently Asked Questions on Regular and Irregular Shapes (FAQs)
How do you know if a shape is regular or irregular?
A regular shape is a two-dimensional (2D) shape whose (interior) angles and sides all have the same measurements, while an irregular shape is a shape with sides and angles of any length and measurement.
It is important to check the sides and angles to differentiate between regular and irregular shapes. If the given shape has the same lengths of sides and angle measurement, it is a regular shape. If the given shape has different lengths of sides and angles measurement, then it is an irregular shape.
What are some examples of regular shapes?
Regular shapes have sides and angles of equal measurements. The following are some examples of regular shapes.

What are some examples of irregular shapes?
Irregular shapes have varying lengths and measurements. Thus, the following are some examples of irregular shapes.

How can I find the perimeter of an irregular shape?
To find the perimeter of irregular shapes, we add together all the lengths of the sides of irregular shapes to find their perimeter.
As an illustration, suppose we need to determine the figure’s perimeter.
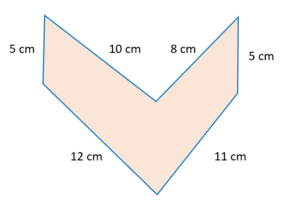
Since the image has six sides with different measurements, it is an irregular hexagon. To find its perimeter, we have,
Perimeter=12 cm+11 cm+10 cm+8 cm+5 cm+5 cm
Perimeter=51 cm
Therefore, the perimeter of the given irregular hexagon is 51 cm.
Recommended Worksheets
Shape Categories (Labor Day Themed) Math Worksheets
Regular and Irregular Shapes (World Oceans Day Themed) Math Worksheets
Symmetrical Shapes (Bodhi Day Themed) Math Worksheets









