Introduction
We have a number of figures in mathematics, which can be used in different sizes and shapes. We can also just change the direction of a figure without changing its shape of size. There are different methods o changing the direction of a figure, one of which is rotation. Some figures remain the same when rotated at different angles while others change their appearance upon rotation. The manner in which a shape remains upon rotation is what defines its rotational symmetry. But, before learning about rotational symmetry, let us first understand what we mean by rotation of a figure.
Rotation of a Figure
Rotation means turning. In mathematics, rotation means turning it about a given point, known as the centre of rotation. The point can be on the figure or at any point. Three things that are needed to describe a rotation are –
- the direction of rotation which may be clockwise or anticlockwise
- the angle of rotation and
- the centre of rotation
Let us understand quotations for an example pillow here we have the rotation of a square of about a given point the square has been further divided into colour squares so as to clearly understand its movement.
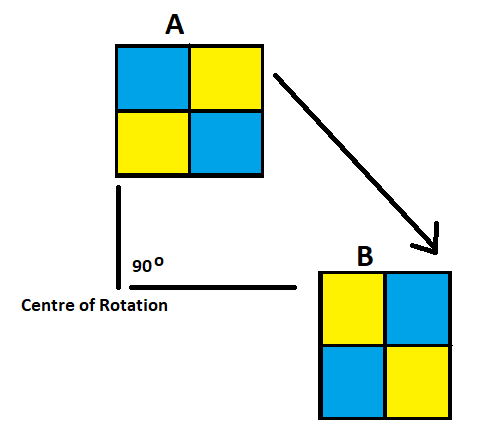
One Quarter Turn
In the above figure, the shape A is rotated through an angle of 90 degrees at the point of the centre of rotation in the clockwise direction to get the shape B. This movement is known as one quarter turn, as we have moved the shape A at 90 degrees which is one quarter of the complete circle, i.e. 360 degrees.
Now, again consider the figure below.
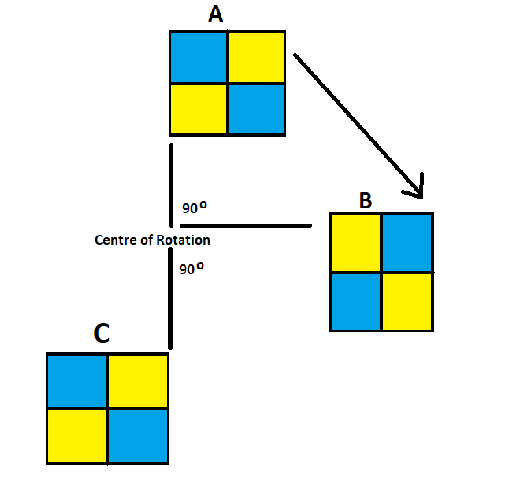
Half Turn
In this figure, the shape B is for rotated through an angle of 90 degrees about the same point of the centre of rotation in the clockwise direction to get the shape C. This is the same as if we would rotate shape A at an angle of 180 degrees about the point of the centre of rotation in the clockwise direction to get shape C. This movement is known as half turn, as we have moved the original shape A at 180 degrees which is half of the complete circle, i.e. 360 degrees.
Again, consider the figure below –
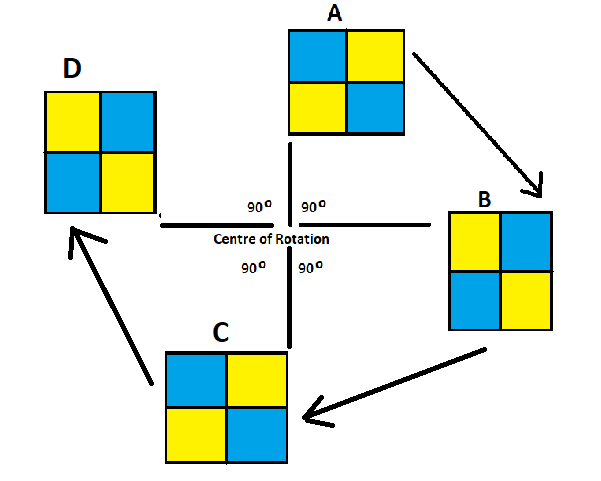
Three Quarter Turn
In the above figure the shape C is again rotated by an angle of 90 degrees about the point of the centre of rotation to get the shape D. This movement is known as three quarter turn, as we have moved the original shape A at 270 degrees which is three quarters of the complete circle, i.e. 360 degrees.
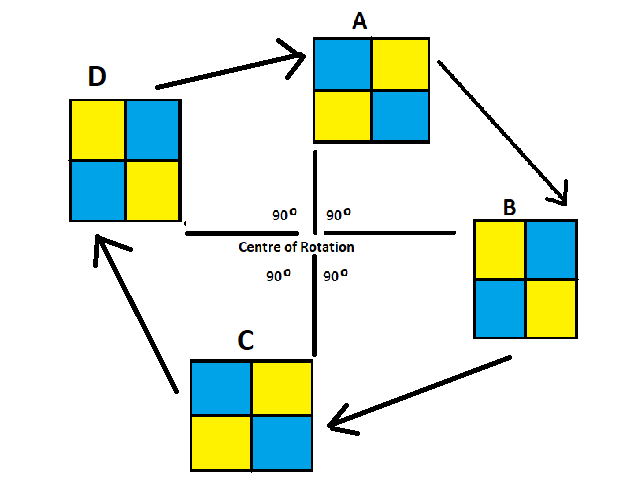
If the shape D is again rotated an angle of 90 degrees about the point of the centre of rotation, we will get back the shape A. This movement is known as the full turn, as we have moved the original shape A at 360 degrees which is a full turn of the complete circle, i.e. 360 degrees.
Angles of Rotation
The angle through which an object rotates ( turns ) about a fixed point is known as the angle of rotation. Depending upon the angle of rotation, these turns can be defined as –
Full Turn – An object is said to take a full turn if the angle of rotation is of 360o.
Half Turn – An object is said to take a half turn, if the angle of rotation is of 180o.
Three Quarters Turn – An object is said to take a three quarters turn if the angle of rotation is of 270o.
Quarter Turn – An object is said to take a quarter turn, if the angle of rotation is of 270o.
Centre of Rotation
The fixed point around which the object rotates is called the centre of rotation. This point could be inside the figure, in which case the figure will remain stationary and will just spin. Alternatively, the point could be outside the figure, causing the figure to move. For example, if a person spins the basketball on the tip of his finger, then the tip of his finger will be considered as rotational symmetry. Now, let us understand, what we mean by rotational symmetry.
Definition
A figure is said to have rotational symmetry if it fits onto itself more than once during a full turn which means rotation through 360o. In other words, if a figure is rotated around a centre point and it still appears exactly as it did before the rotation, it is said to have rotational symmetry. Consider a rotating object, say a wheel of a bicycle or a windmill etc. the fixed point about which the object rotates is called the centre of rotation. When an object rotates in the direction of motion of the hands of a clock, rotation is called clock wise rotation, otherwise it is said to be anti-clockwise rotation.
Order of Rotational Symmetry
The number of times any shape or an object that can be rotated and yet looks similar as it was before the rotation is known as the order of rotational symmetry. In other words, The number of times a figure fits into itself in one complete rotation is called the order of rotational symmetry.
Formula for Finding Order of Rotational Symmetry
The formula for Finding Order of Rotational Symmetry is given by –
Order of Rotational Symmetry = $\frac{360}{Angle of Rotation}$
This means that a figure has a rotational symmetry of order 1, if it can come to its original position after full rotation or 360°. Let us learn about the orders of rotational symmetry of different objects.
Rotational Symmetry vs Line Symmetry
We have learnt that rotational symmetry is said to occur in an image if it fits onto itself more than once during a full turn which means rotation through 360o. We have also heard the term lien symmetry. How are these two different from each other? Let us find out.
| Line Symmetry | Rotational Symmetry |
| The ‘Line of Symmetry’ is the imaginary line where you could fold the image and have both halves matching exactly. | Rotational symmetry is when an object is rotated around a centre point (turned) by a number of degrees and the object appears the same. The order of symmetry is the number of positions the object looks the same in a 360° rotation. |
| To find whether or not a given figure is symmetrical about a line in it, fold the figure about that line. | To find the rotational symmetry of a given figure, we rotate it through 360o |
Rotational Symmetry of Order 1
A figure has a rotational symmetry of order 1, if it can come to its original position after full rotation or 360°.
Let us understand it by an example.
Consider the following shape –

We can see that the above figure is of the shape of a kite. Since the kite has one line of symmetry, therefore, it has a rotational symmetry of the order 1.
Let us take another example.
Consider the following shape –
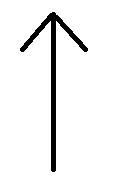
The above shape when rotated cannot come back to its original form until it goes through a complete turn of 180o. Hence the order of rotational symmetry of this shape is 1.
Rotational Symmetry of Order 2
A figure has a rotational symmetry of order 2, if it can come to its original position after half rotation or 180°.
Let us understand it by an example.
Consider the following shape –
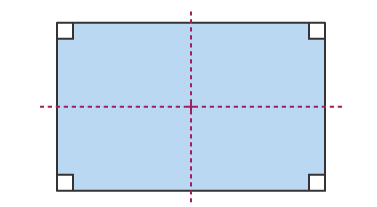
We can see that the above figure is of the shape of a rectangle. Since the rectangle has two lines of symmetry, therefore, it has a rotational symmetry of the order 2.
Let us take another example.
Consider the following shape –
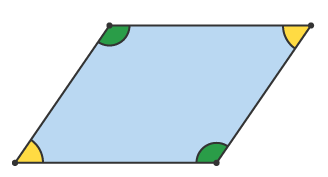
We can see that the above figure is of the shape of a parallelogram. Since the parallelogram has two lines of symmetry, therefore, it has a rotational symmetry of the order 2.
Rotational Symmetry of Order 3
A figure has a rotational symmetry of order 3, if it can come to its original position after each 120 degrees rotation.
Let us understand it by an example.
Consider the following shape –
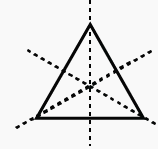
We can see that the above figure is of the shape of an equilateral triangle. Since an equilateral triangle has three lines of symmetry, therefore, it has a rotational symmetry of the order 3.
Rotational Symmetry of Order 4
A figure has a rotational symmetry of order 4, if it can come to its original position after quarter rotation or 90°.
Let us understand it by an example.
Consider the following shape –
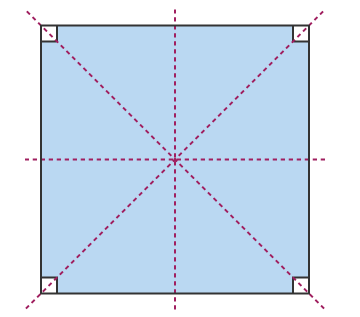
We can see that the above figure is of the shape of a square. Since the square has four lines of symmetry, therefore, it has a rotational symmetry of the order 4.
Rotational Symmetry of Order 6
A figure has a rotational symmetry of order 6, if it can come to its original position after quarter rotation or 60°.
Let us understand it by an example.
Consider the following shape –
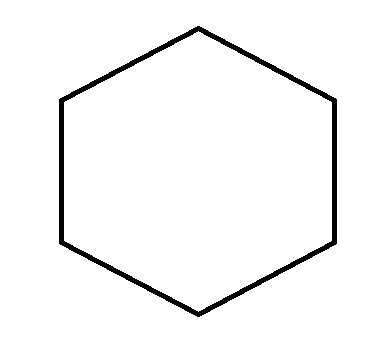
We can see that the above figure is of the shape of a hexagon. Since the hexagon has six lines of symmetry, therefore, it has a rotational symmetry of the order 6.
Rotational Symmetry of Order 8
A figure has a rotational symmetry of order 8, if it can come to its original position after quarter rotation or 45°.
Let us understand it by an example.
Consider the following shape –

We can see that the above figure is of the shape of an octagon. Since the octagon has eight lines of symmetry, therefore, it has a rotational symmetry of the order 8.
Below we have a table that summarises order of rotational symmetry of some common shapes –
| Name of the Shape | Order of Rotational Symmetry |
| Parallelogram | 2 |
| Rhombus | 2 |
| Circle | Infinite |
| Kite | 2 |
| Square | 4 |
| Rectangle | 2 |
| Hexagon | 6 |
| Octagon | 8 |
Rotational Symmetry of Alphabets
Rotational symmetry in English alphabets refers to the fact that the letter retains its appearance after being rotated. Let us observe some English alphabets that demonstrate rotational symmetry.
- Consider the alphabet “ B “. If we rotate the alphabet “ B “ to 360o, we will notice that it gets back to its original position. Moreover, since the alphabet “ B “ has one line of symmetry, therefore, it has a rotational symmetry of the order 1.
- Consider the alphabet “ F “. If we rotate the alphabet “ F “ to 360o, we will notice that it gets back to its original position. Moreover, since the alphabet “ F “ has one line of symmetry, therefore, it has a rotational symmetry of the order 1.
- Consider the alphabet “ H “. If we rotate the alphabet “ H “ to 180o, we will notice that it gets back to its original position. Moreover, since the alphabet “ H “ has two lines of symmetry, therefore, it has a rotational symmetry of the order 2.
- Consider the alphabet “ S “. If we rotate the alphabet “ S “ to 180o, we will notice that it gets back to its original position. Moreover, since the alphabet “ S “ has two lines of symmetry, therefore, it has a rotational symmetry of the order 2.
- Consider the alphabet “ N “. If we rotate the alphabet “ N “ to 180o, we will notice that it gets back to its original position. Moreover, since the alphabet “ N “ has two lines of symmetry, therefore, it has a rotational symmetry of the order 2.
- Consider the alphabet “ X “. If we rotate the alphabet “ X “ to 90o, we will notice that it gets back to its original position. Moreover, since the alphabet “ X “ has four lines of symmetry, therefore, it has a rotational symmetry of the order 4.
Solved Examples
Example 1 What is the angle of rotational symmetry for a shape that has rotational symmetry of order 5?
Solution We have been asked to determine what would be angle of rotational symmetry for a shape that has rotational symmetry of order 5. Let us recall that the angle of the rotational symmetry is the smallest angle for which the given figure can be rotated and coincides with itself. Also, the order of the symmetry is the number of times the figure coincides and rotates through 360∘ and the figure looks exactly the same.
Now, we have learnt that that
Order of Rotational Symmetry = $\frac{360}{Angle of Rotation}$
Since, we have been order of rotational symmetry as 5, substituting this value in the above equation, we get,
Angle of Rotation = $\frac{360}{5}$ = 72o
Hence, the angle of rotational symmetry for a shape that has rotational symmetry of order 5 will be 72o.
Example 2 What will be the order of rotational symmetry of the recycle logo?

Solution We have been given the recycle logo and we are required to determine its order of symmetry. We can clearly see that the arrows of the recycle logo appear to be moving in a circular manner, suggesting the circular concept of recycling. Adding to this perception is that if you were to rotate the image 120 degrees, and another 120 degrees, and a third 120 degrees, it would look the same at all three stops. This means that the order of symmetry of the recycle logo will be 3.
Hence, the order of symmetry of the recycle logo will be 3.
Key Facts and Examples
- Rotation means turning. In mathematics, rotation means turning it about a given point, known as the centre of rotation.
- Three things that are needed to describe a rotation are the direction of rotation which may be clockwise or anticlockwise, the angle of rotation and the centre of rotation.
- A figure is said to have rotational symmetry if it fits onto itself more than once during a full turn which means rotation through 360o.
- The angle through which an object rotates or turns about a fixed point is known as the angle of rotation.
- An object is said to take a full turn, if the angle of rotation is of 360o.
- An object is said to take a half turn, if the angle of rotation is of 180o.
- An object is said to take a three quarters turn, if the angle of rotation is of 270o.
- An object is said to take a quarter turn, if the angle of rotation is of 270o.
- The number of times any shape or an object that can be rotated and yet looks similar as it was before the rotation is known as the order of rotational symmetry.
- The ‘Line of Symmetry’ is the imaginary line where you could fold the image and have both halves matching exactly.
- A figure has a rotational symmetry of order 1, if it can come to its original position after full rotation or 360°.
- A figure has a rotational symmetry of order 2, if it can come to its original position after half rotation or 180°.
- A figure has a rotational symmetry of order 3, if it can come to its original position after each 120 degrees rotation.
- A figure has a rotational symmetry of order 4, if it can come to its original position after quarter rotation or 90°.
- Rotational symmetry in English alphabets refers to the fact that the letter retains its appearance after being rotated.









