Perpendicular Lines

Introduction

Before we understand what we mean by perpendicular lines, we must first recall the basic concepts and terms that are integral to the understanding of perpendicular lines. Therefore, let us recall some basic concepts of geometry. For instance, a point is an exact location in space. It has no length and no width. 

Similarly, an angle is a figure formed by two rays with the same initial point. In geometry, different names are given to different angels and their combinations depending upon the type of angles they make. Different geometrical shapes such as a triangle or a quadrilateral contain a set of angles that are governed by a set of rules. For example, there are three interior angles in a triangle, the sum of which is always equal to 180^o. This means that if we are aware of two of the angles in a triangle we can find the third. Similarly using different rules and the available information we can find the missing angle in a geometrical figure.

Definition

Perpendicular lines are the two distinct lines that intersect at each other at 90°. In the below figure, we can see that there are two lines, AB and XY that intersect each other at 90^o. Hence, lines AB and XY are said to be perpendicular to each other.  

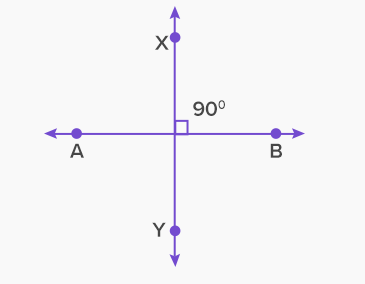
How do we represent two perpendicular lines? In other words, what is the symbol used to represent two perpendicular lines?

Symbol for representing Perpendicular Lines

The symbol is used to represent lines that are perpendicular to each other. So, if we wish to say that the lines AB and XY are perpendicular to each other, we can simply write them as AB XY

Measure of Perpendicular Lines

The angle between two lines that are perpendicular to each other is always 90^o. 

Properties of Perpendicular Lines

The following are the general properties of perpendicular lines-  

1. Perpendicular lines always meet or intersect each other.
2. Perpendicular lines always intersect at the right angle, i.e. 90^o.
3. If two lines are perpendicular to the same line, then they both are parallel to each other and never intersect.

Perpendicular Lines and Straight angles

We know that a straight angle is an angle, whose vertex point has a value of 180 degrees. In other words, a straight angle is an angle that forms a straight line. Can we form a straight angle using a combination of perpendicular lines? Carefully observe the description of a straight angle – 

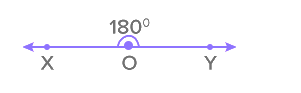
We can see that a straight angle can be formed by a pair of angles that sum up to 180^o.  If we join two pairs of perpendicular lines in the below manner, we shall obtain a straight angle.  

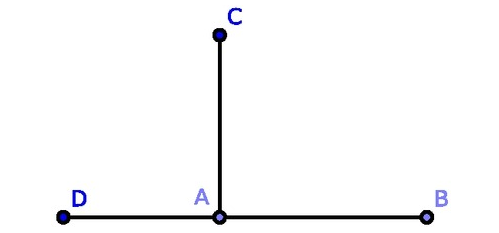
In the above figure, the lines AB ⊥ AC. Also, AC ⊥ AD. But both the pair together form a straight angle ∠ DAB which measures 180^o. Hence, two perpendicular lines can be used to make one straight angle. 

Now, let us learn about different geometrical figures that can be formed using perpendicular lines.

Triangles formed using Perpendicular Lines 

We now know that two lines are perpendicular if they form an angle of 90^o with each other. Now, if we have another line that joins these two lines, we form a triangle. What do we call such a type of triangle?  Such an angle is called a right angled triangle. 

Also, if one of the angles of a triangle is 90^o, the sides that make the right angle are called the base and the perpendicular while the third side is called the hypotenuse.

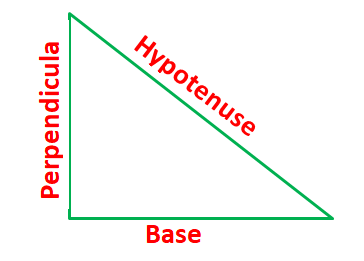
According to Pythagoras Theorem

In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides.

Mathematically,

Base² + Perpendicular² = Hypotenuse²

Therefore, if “a” is the base, “b” is the perpendicular and “c” is the hypotenuse in a right angled triangle, then

c² = a² + b²

Moreover, We know that there are three interior angles in a triangle. Now, with one of the angles being 90^o, we have two lines as perpendicular to each other, the sum of the remaining two angles will be 90^o.  Based on the measure of these two remaining angles, there are two types of right angled triangles – 

1. Right Scalene Triangle
2. Right Isosceles Triangle

Right Isosceles Triangle

A triangle is said to be a right isosceles triangle if apart from two sides being equal, one of the angles of the triangle is a right angle, i.e. 90^o_. Suppose, we have a triangle, ABC where AB = BC and ∠ABC = 90^o.  Then such a triangle is called a right isosceles triangle which would be of a shape similar to the below figure.

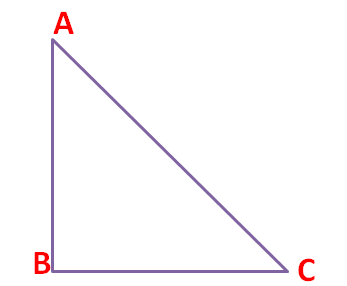
Right Scalene Triangle

A triangle is said to be a right scalene triangle if apart from no side of it being equal, one of the angles of the triangle is a right angle, i.e. 90^o_. Suppose, we have a triangle, ABC where AB ≠ BC ≠ CA and ∠ABC = 90^o.  Then such a triangle is called a right scalene triangle which would be of a shape similar to the below figure.

Quadrilaterals formed using Perpendicular Lines 

We know that a quadrilateral is a closed shape that is formed by joining four points among which any three points are non-collinear. Some standard quadrilaterals are made using perpendicular lines. Let us learn about some of these shapes – 

Let us now learn about different types of quadrilaterals.  

Rectangle

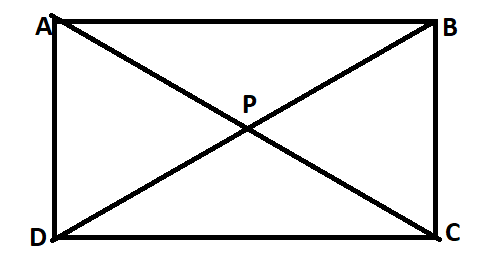
A rectangle is a type of quadrilateral that has equal opposite sides and four right angles. A rectangle has two pairs of parallel sides. A rectangle has four right angles. A rectangle has opposite sides of equal lengths. The diagonals of a rectangle bisect each other. A unique characteristic of a rectangle is that all its edges are perpendicular lines. 

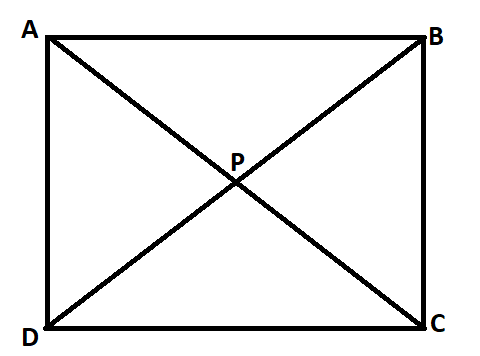
Square

A square is a quadrilateral that has four equal sides and four right angles. A square has four equal sides, i.e. all the sides of a square are equal. A square has four right angles. A square has two pairs of parallel sides.  The diagonals of a square bisect each other. The diagonals of a square are perpendicular to each other. A unique characteristic of a square is that all its edges are perpendicular lines. 

Rhombus

A rhombus is a quadrilateral with four equal sides. A rhombus has two pairs of parallel sides. The opposite angles in a rhombus are equal. A rhombus has four equal sides. This means that all its sides are equal. The diagonals of a rhombus bisect each other. The diagonals of a rhombus are perpendicular each other.

Slope of Perpendicular Lines

We know that a straight line is a curve such that every point on the line segment joining any two points on it lies on it. Also, the trigonometrical tangent of the angle that a line makes with the positive direction of the x-axis in an anticlockwise sense is called the slope or the gradient of a line. Perpendicular lines have slopes that are negative reciprocals of one another.

Can Complementary angles or Supplementary angles form perpendicular lines?

Perpendicular lines are an integral component of geometrical calculations. Other than making shapes, their use is also found in complementary angles and supplementary angles. Let us first recall what we mean by complementary angles and supplementary angles. Two angles are said to be complementary if their sum is 90^o. For example, two angles, 30^o and 60^o are complementary because their sum, 30^o + 60^o = 90^o. Similarly, two angles are said to be supplementary if their sum is 180^o. For example, two angles, 130^o and 50^o are supplementary because their sum, 130^o + 50^o = 180^o. Together, the supplementary angles form a straight line. Observe the following figure – 

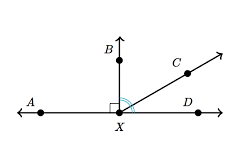
In the above figure, we can notice that the angles ∠ CXD and ∠ CXB form a pair of right angle. Now,

The sum of the angles ∠ CXD and ∠ CXB will be 90^o. This means that the lines, BX and XD are perpendicular to each other. Hence, we can say that a pair of complementary angles having a common arm consists of a pair of perpendicular lines as well. 

Similarly, observe the angles ∠ BXD and ∠ BXA.

The sum of the angles ∠ BXD and ∠ BXA will be 180^o. Also, we can see that the lines XD and XA form a straight line. Therefore, we can say that we can have a pair of angles that form a straight line and consist of two pair of perpendicular lines as well.  

Perpendicular Lines vs Parallel Lines

We know that two lines l and m in the same plane are said to be parallel lines of they do not intersect when produced indefinitely in either direction. How are parallel lines different from perpendicular lines? Let us find out.

Parallel Lines	Perpendicular Lines
The distance between a pair of parallel lines always remains the same. This means that parallel lines are always the same distance apart from each other.	Perpendicular lines always intersect each other at right angles.
Symbolically, two parallel lines l and m are written as l || m.	The symbol is used to represent lines that are perpendicular to each other.
Example of parallel lines –  Railway tracks	Example of perpendicular lines – corner of two walls

Perpendicular Lines in Real Life

Perpendicular lines are not only meant for geometrical constructions. They are widely used in real life situations as well. Following are the some of the areas / sectors where the concept of perpendicular lines is widely used – 

1. Carpenters, builders, and furniture makers depend on perpendicular lines to create flat surfaces and buildings that stand up straight.
2. A tool known as set square is used by woodworkers to draw perpendicular lines.
3. The corner of two walls is also an example of perpendicular lines.
4. The stumps of a wicket in cricket are placed on the ground at right angles from the ground.

Solved Examples

Example 1 Find the measures of the angles x, y and z in the following figure – 

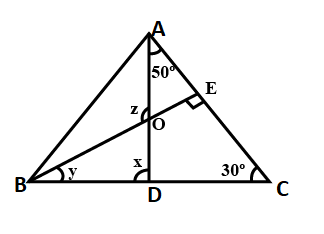
Solution We have been a figure where some of the angles are known while we are required to find the values of the angles x, y and z. 

Now, let us consider the ∆ BEC. 

We know that the sum of the measure of the three interior angles of a triangle is always 180^o.

Therefore,

∠ BEC + ∠ EBC  + ∠ ECB = 180^o …………………………… ( 1 )

Now, we have been given that,

∠ BEC = 90^o

∠ ECB = 30^o

∠ EBC  = y

Substituting these values in equation ( 1) we will get,

y + 90^o + 30^o= 180^o

⇒ y + 120^o= 180^o

⇒ y = 180^o – 120^o

⇒ y = 60^o

Now, let us consider ∆ AC. 

Again, we will use that property that the sum of the measure of the three interior angles of a triangle is always 180^o.

Therefore,

∠ ADC + ∠ ACD  + ∠ DAC = 180^o …………………………… ( 2 )

Now, we have been given that,

∠ DAC = 50^o

∠ ACD = 30^o

Substituting these values in equation ( 2) we will get,

∠ ADC + 50^o + 30^o= 180^o

⇒ ∠ ADC + 80^o= 180^o

⇒ ∠ ADC = 180^o – 80^o

⇒ ∠ ADC = 100^o

Now that we know the value of ∠ ADC, we can find the value of ∠ ADB.

We can see that ∠ ADC and ∠ ADE form a supplementary [air of angles. We also know that the sum of supplementary angles is always equal to180^o. Therefore,

∠ ADC + ∠ ADE = 180^o …………………….. ( 3 )

We have been given that 

∠ ADE =  x and we have obtained above that

∠ ADC = 100^o

Substituting these values in equation ( 3 ) we will get,

100^o + x = 180^o

⇒ x = 180^o – 100^o

⇒ x = 80^o

Now, let us consider the ∆ AOB. We can clearly see that the angle z is an exterior angle for the two angles x and y. by the definition of the exterior angle property of a triangle, The exterior angle of a triangle is always equal to the sum of the interior opposite angles. Therefore, we can say that

∠ z  =  ∠ x  + ∠ y  ………………………. ( 4 )

We have already obtained the values of and y above as – 

x = 80^o

y = 60^o

Substituting these values in equation ( 4 ) we will get,

z = 80^o + 60^o 

⇒ z = 140^o 

Thus, we have the values of x, y and z we have as – 

x = 80^o

y = 60^o

z = 140^o 

Example 2 A line perpendicular to the line segment joining the points (1, 0) and ( 2, 3 ) divides it in the ratio 1:2. Find the equation of the line.

Solution We have been given that the points are(1, 0) and ( 2, 3 ) and the line perpendicular to the line segment divides it in the ratio of 1 : 2.

 Let M divide the join of A(1,0) and B(2,3) in the ratio of 1:2

Then, the point M is (1 x 2+2 x 11+2, 1 x 3+2 x 01+2 ) 

Hence, M= (43, 1 )

Slope of the line AB= 3-0 2-1 = 3

Let L be the required line. Then, the slope of L= -1  3 and it passes through M 

Now, let L be the required line. we have been given that L is perpendicular to AB.

Therefore, 

Slope of L= -1  3  and it passes through M (43, 1 )

Since now we have one point as well as the slope of the line, we can use the point-slope form to find the equation of the line.

We know that the equation of the line in point-slope form is 

y-y1 = m (x-x1)

Substituting the given values in the above equation, we have

Therefore, the required equation of the straight line is 

y-1 = -1  3   (x-43)

9 ( y – 1 ) = -1 ( 3x – 4 )

⇒ 9y – 9 = -3x + 4

⇒ 3x + 9y – 13 = 0

Hence, the equation of the line that is perpendicular to the line segment joining the points (1, 0) and ( 2, 3 ) and divides it in the ratio 1:2 will be given by 3x + 9y – 13 = 0

Key Facts and Summary

1. Perpendicular lines are the two distinct lines that intersect at each other at 90°.
2. The symbol is used to represent lines that are perpendicular to each other.
3. The angle between two lines that are perpendicular to each other is always 90^o. 
4. Perpendicular lines always meet or intersect each other.
5. Perpendicular lines always intersect at the right angle, i.e. 90^o.
6. If two lines are perpendicular to the same line, then they both are parallel to each other and never intersect.
7. Two perpendicular lines can be used to make one straight angle. 
8. A triangle is said to be a right isosceles triangle if apart from two sides being equal, one of the angles of the triangle is a right angle, i.e. 90^o_.
9. A triangle is said to be a right scalene triangle if apart from no side of it being equal, one of the angles of the triangle is a right angle, i.e. 90^o_.
10. A pair of complementary angles having a common arm consists of a pair of perpendicular lines as well.

Recommended Worksheets

Spatial Skill: Lines, Segments, and Rays (International Day of PWDs Themed) Worksheets
Spatial Skills: Triangles and Quadrilaterals (Winter Solstice Themed) Math Worksheets
Complementary Angles (Lantern Festival Themed) Math Worksheets