Introduction
In the amazing world of mathematics, there are a lot of unique shapes that we can observe. The icosahedron is one of the most fascinating three-dimensional shapes there is. The name “icosahedron,” which derives from the Greek terms “íkosi” (which means twenty) and “hédra” (which implies seat or face), describes a fascinating shape with special features that is an integral part of the world we live in.
Grade Appropriateness
Despite being a high-grade subject, kids between the ages of 8 and 15 can understand the study of an icosahedron. It is typically introduced to kids in middle school arithmetic as they learn about geometry and three-dimensional shapes.
Math Domain
The icosahedron falls within the scope of Geometry, a field of mathematics that deals with size, shape, relative placement of objects, and spatial characteristics.
Applicable Common Core Standards
The study of the icosahedron is aligned with the following Common Core standards:
CCSS.MATH.CONTENT.5.G.B.3 – Understand that attributes belonging to a category of two-dimensional figures also belong to all subcategories of that category.
CCSS.MATH.CONTENT.5.G.B.4 – Classify two-dimensional figures in a hierarchy based on properties.
CCSS.MATH.CONTENT.6.G.A.4 – Represent three-dimensional figures using nets made up of rectangles and triangles, and use the nets to find the surface area of these figures.
Definition of the Topic
A polyhedron is a three-dimensional form with flat sides and straight edges, and the icosahedron is one of them. But this particular polyhedron is not just any polyhedron but a special kind known as a Platonic Solid. The icosahedron is one of the five Platonic Solids known to exist.
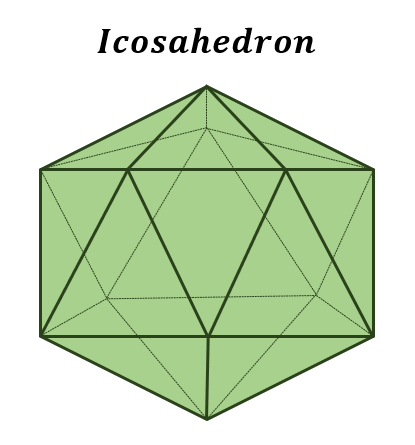
So, what makes an icosahedron unique? It has 20 faces, all identical equilateral triangles, 12 vertices (corners), and 30 edges. Each vertex of an Icosahedron is where five triangles meet.
Key Concepts
Regular Icosahedron: A regular icosahedron has 20 faces that are equilateral triangles. In a regular icosahedron, all 30 edges are of equal length and have 12 vertices.
Faces: The flat surfaces of the icosahedron are called faces. In an icosahedron, there are 20 faces, and each one is an equilateral triangle.
Vertices: The points where the faces of the icosahedron meet are called vertices. In an Icosahedron, there are 12 vertices.
Edges: The line segments where two faces meet are called edges. In an icosahedron, there are 30 edges.
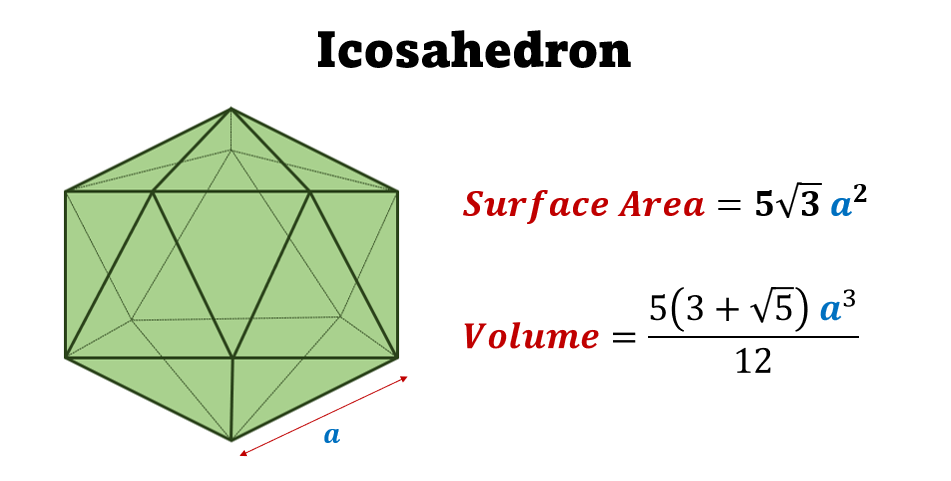
The volume of Icosahedron: The formula to calculate the volume of a regular icosahedron is
Volume=$\frac{5(3+\sqrt{5})}{12}$a3, where a is the length of the edge.
Total surface area of Icosahedron: The formula to find the total surface area of a regular icosahedron is:
Total Surface Area=$5\sqrt{3}$ a2, where a is the length of the edge.
Discussion with Illustrative Examples
A platonic solid called an icosahedron has twenty equilateral triangular faces. It belongs to the group of five regular polyhedra known as the platonic solids, which include the tetrahedron, cube, octahedron, icosahedron, and dodecahedron.
An easy way to visualize an Icosahedron is to think about a d20 dice, commonly used in tabletop games like Dungeons and Dragons. The dice are shaped like an Icosahedron – each face numbered 1 to 20.
Parts of Icosahedron
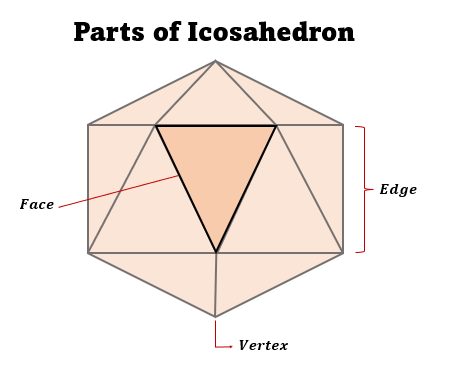
The vertex is the point of intersection of five edges.
The face is the flat surface of an icosahedron.
The edge is the line where two adjacent faces meet.
Properties of Icosahedron
To help us identify this shape, the following are the properties of an icosahedron:

An icosahedron has 20 faces. Each face is an equilateral triangle, meaning all sides and angles are equal.
An edge is the section of a line where two faces intersect. An icosahedron has 30 edges—the angle between the edges of an icosahedron measures 60°.
The corners of an icosahedron, where the faces meet, are called vertices. There are 12 vertices in an icosahedron. There are five faces at each vertex.
Icosahedron has the most number of faces among all platonic solids.
Icosahedron has the largest volume among all platonic solids for its surface area.
Nets of Icosahedron
An icosahedron can be made using a geometric net. A net is a two-dimensional shape in geometry that takes on a three-dimensional appearance when folded in a particular way.
Folding the following geometric nets shown below will result in the formation of an icosahedron.

Formulas Involving Icosahedron
Total Surface Area of an Icosahedron
The total surface area of a regular icosahedron is the surface area of all its faces. An equilateral triangle has an area of A=$\frac{\sqrt{3}}{4}$ a2 where a is the edge length. Since there are 20 equilateral triangles in an icosahedron, we have,
Total Surface Area=20×$\frac{\sqrt{3}}{4}$ a2
Therefore, the formula for calculating the total surface area of a regular icosahedron is:
Total Surface Area
Icosahedron=5√3 a2, where a is the length of the edge.
The total surface area of an icosahedron is expressed in square units.
Volume of an Icosahedron
The volume of a regular icosahedron is the total space it occupies in a three-dimensional plane. The formula for calculating the volume of a regular icosahedron is given by:
VolumeIcosahedron=$\frac{5(3+\sqrt{5}) a^3}{12}$, where a is the length of the edge.
The volume of a regular icosahedron is expressed in cubic units.
Examples with Solution
Example 1
Find the surface area of an icosahedron whose edge length is 4 inches.
Solution
Let us substitute the given edge length, a=4 inches, into the formula.
Total Surface Area=5√3 a2 (Formula)
Total Surface Area=5√3 (4)2 (Substitution)
Total Surface Area=80√3 (Simplify)
Total Surface Area≈138.56
Hence, the surface area of an icosahedron with an edge length of 4 inches is 138.56 in2.
Example 2
Calculate the volume of an icosahedron whose edge length measures 8 centimetres.
Solution
Using the given edge length, a=8 cm, we have,
Volume=$\frac{5(3+\sqrt{5})}{12}$a3 (Formula)
Volume=$\frac{5(3+\sqrt{5})}{12}$ (8)3 (Substitution)
Volume≈1117.03
Therefore, the volume of an icosahedron whose edge length measures 8 cm is 1117.03 cm3.
Example 3
If the total surface area of a regular icosahedron is 405√3 square units, find its volume.
Solution
Since we know that the total surface area is 405√3 square units, let us first calculate the edge length of the icosahedron. Using the formula for getting the total surface area we have,
5√3 a2=405√3
$\frac{5\sqrt{3}a^2}{5\sqrt{3}}$=$\frac{405\sqrt{3}}{5\sqrt{3}}$ (Dividing both sides by 5$\sqrt{3}$)
a2=81 (Simplify)
√a=√81
a=9 units (Edge length)
Now, using the formula for getting the volume of a regular icosahedron, we shall have,
Volume=$\frac{5(3+\sqrt{5})}{12}$a3 (Formula)
Volume=$\frac{5(3+\sqrt{5})}{12}$ (9)3 (Substitution)
Volume≈1590.46
Therefore, the volume of a regular icosahedron is 1590.46 cubic units if TSA is 405√3 square units.
Real-life Application with Solution
Problem 1
The edge of an icosahedron-shaped banner is 4.5 centimetres. Determine its surface area.
Solution
Surface Area=5√3 a2 (Formula)
Surface Area=5√3 (4.5)2 (Substitution)
Surface Area=101.25√3 (Simplify)
Surface Area≈175.37
Hence, the surface area of the icosahedron-shaped banner is 175.37 cm2.
Problem 2
Find the volume of an icosahedron-shaped water bomb whose edge measures five units.
Solution
Volume=$\frac{5(3+\sqrt{5})}{12}$a3 (Formula)
Volume=$\frac{5(3+\sqrt{5})}{12}$ (5)3 (Substitution)
Volume≈272.71
Therefore, the volume of the icosahedron-shaped water bomb is 272.71 cubic units.

In conclusion, the icosahedron is an exciting shape to learn about, offering a great way to explore the world of Geometry. It’s not just an abstract mathematical concept but a shape found in nature and used in everyday life. So, the next time you’re rolling a d20 or hitting a golf ball, remember the icosahedron!
Practice Test
1. How many faces does an Icosahedron have?
2. What shape are the faces of an Icosahedron?
3. How many vertices does an Icosahedron have?
4. How many edges does an Icosahedron have?
5. Calculate the surface area and volume of a regular icosahedron whose edge length measures 10 cm.
Answers:
1. 20 faces
2. Equilateral triangle
3. 12 vertices
4. 30 edges
5. Surface Area=866.03 cm2; Volume≈2181.69 cm3
Frequently Asked Questions (FAQs)
What are the other Platonic Solids?
Besides the icosahedron, there are four other Platonic Solids: Tetrahedron, Cube, Octahedron, and Dodecahedron.
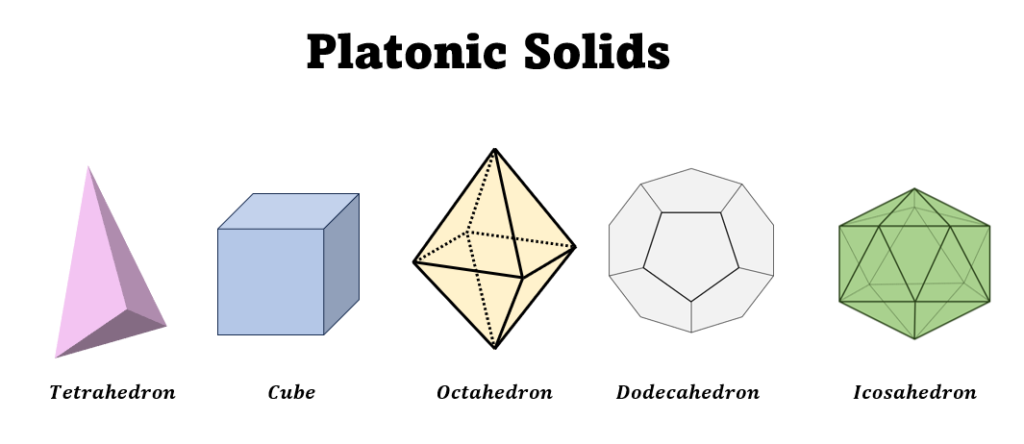
What is the difference between an Icosahedron and a Dodecahedron?
The main difference is that a Dodecahedron has 12 faces that are regular pentagons, while an Icosahedron has 20 faces that are equilateral triangles.
Why is an Icosahedron called a Platonic Solid?
Platonic solids have faces that are all identical, regular polygons meeting at the same three-dimensional angles. An icosahedron has twenty congruent triangular faces – equal length edges and equal angle measures.
Can an Icosahedron be made from any triangle?
No. An Icosahedron’s faces are explicitly made from equilateral triangles – those where all sides and angles are equal.
Are all the faces of an Icosahedron the same?
Yes. One of the key properties of the icosahedron, and indeed all Platonic Solids, is that all of their faces are congruent, meaning they are identical in shape and size.
Recommended Worksheets
Icosahedron (Holi Themed) Math Worksheets
Platonic Solids (Earth Day Themed) Math Worksheets
Drawing And Describing 2D And 3D Figures 7th Grade Math Worksheets









