What Is Division?

Division is the equal sharing of a given quantity.

For example, Alice wants to share 6 bananas equally with her friend Rose. So, she gives 3 of her bananas to Rose and she is also left with 3 bananas. This means that when we divide 6 by 2 we get 3.

Mathematically, we can write this as

6 ÷ 2 = 3

In mathematics, there is a symbol for every operation. The symbol for division is (÷). Other than the forward-slash (/) is also used to denote the division of two numbers, where, the dividend comes before the slash and the divisor after it. For instance, if we wish to write 15 is being divided by 3, we can write it as 15 ÷ 3 or 15 / 3. Both mean the same.

Important terms in Division

The number that is to be divided is called the Dividend. Here, 6 is the dividend.

The number by which the dividend is being divided is called the Divisor.

The result obtained by the process of division is called the Quotient.

The number that is left over after finding the quotient is called the Remainder.

Let us understand these by an example.

Suppose, we have a pack of 65 chocolates and we want to divide them equally among 7 children while keeping the remaining chocolates with us. How many chocolates does each child get and how many chocolates are we left with after dividing these chocolates?

Using multiplication tables, we have 7 x 9 = 63

Therefore, 7 x 9 + 2 = 65

This means that the quotient when 65 is divided by 7 will be 9 and the remainder will be 2.

As per the definition of the four terms of division, we have

Divisor = 7

Dividend = 65

Quotient = 9

Remainder = 2

Remember: The remainder is always smaller than the divisor.

Formula for Division

There are four important terms in the division, namely, divisor, dividend, quotient, and the remainder. The formula for divisor constitutes all of these four terms. In fact, it is the relationship of these four terms among each that defines the formula for division. If we multiply the divisor with the quotient and add the result to the remainder, the result that we get is the dividend. This means,

Dividend = Divisor x Quotient + Remainder

Checking Your Result

In division, it is always possible to check whether the result obtained is correct or not. The formula for division helps us to check our results as well. for instance, let us divide 7 by 2. We will get the quotient as 3 and the remainder as 1. Now, if we wish to verify our result, we just place the values in the formula. This means,

7 = 2 x 3 + 1

7 = 7

Since, LHS = RHS, we can say that our result is correct. In case we find that LHS ≠ RHS, this means that there is some error in our division and either the quotient or the remainder is incorrect and we need to revisit our solution.

Long Division

While it is quick and easy to divide a one-digit number, there are certain steps involved for larger numbers. This is called long division. Let us understand these steps using some examples. The steps involved for dividing a number by another depending on the digits of the dividend and the divisor. Let us understand these using some examples.

Suppose we wish to divide 78 by 6.

Compare the first digits of both the dividend and the divisor. The digit of the dividend is greater than that of the divisor. Therefore, in cases where the first digit of the dividend is equal to or greater than the divisor, the following steps should be followed –

Since 7 > 6 we can easily divide it by 6 leaving the remainder 1.

On subtracting 6 from 7 we get the remainder as 1.

Now, consider the second digit of the dividend which is 8. Combining 1 with 8 we get 18.

Now divide 18 by 6 and we get 3 as the quotient, leaving the remainder as 0 as 6 fully divides 18.

Therefore, 78 ÷ 6 = 13

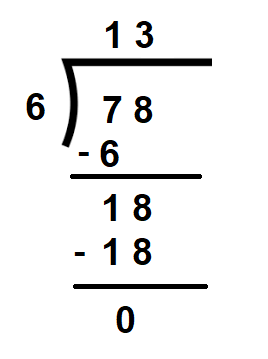
Now let us consider a case where the first digit of the dividend is less than that of the divisors.

Suppose, we wish to divide 426 by 8

Now, 4 < 8. Therefore, we will have to consider the first two digits of the dividend to divide by 8 in the first step.

We, therefore, take the first two digits, i.e. 42, and divide them by 8. We get 5 as the quotient and 2 as the remainder.

Next, we take consider the digit of the dividend, i,e, 6. Combing 2 with 6 we get the number 26.

Now, we divide 26 by 8 in which we get 3 as the quotient and 2 as the remainder.

Hence 426 ÷ 8 = 53, remainder = 2

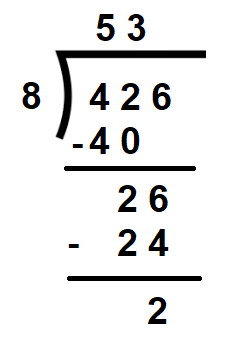
Division of a four-digit number by a one-digit number

Let us divide 4356 by 3

Here,

3 is the divisor and 4356 is the dividend. The following are the steps involved in dividing 4356 by 3.

Step 1: Divide 4 by 3.

3 x 1 = 3. Thus quotient is equal to 1 and the remainder is equal to 1. This can be represented mathematically as,

Step 2: Bring down the next digit 3. Write along with the remainder 1 as 13 and divide 13 by 3. We get the quotient as 4 and the remainder as 1.

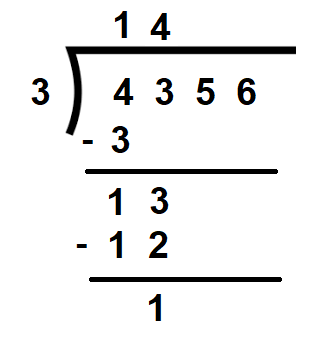
Step 3: Now, bring down the next digit 5 which is the hundred’s place. Write it along with the reminder 1 as 15 and divide 15 by 3. We get the quotient as 5 and the remainder as 0.

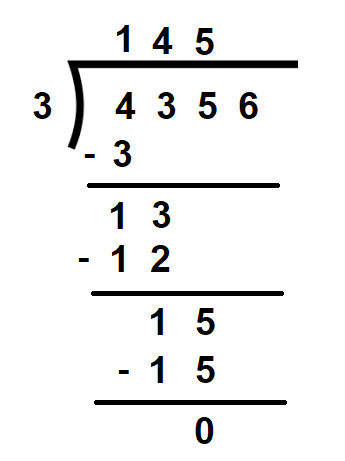
Step 4: Bring down the last digit 6 and divide 6 by 3. We get the quotient as 2 and the remainder as 0.

Since there are no further digits left to be divided, we have the quotient as 1452 and the remainder as 0

This can also be written as 4356 ÷3 = 1452

Division of a four-digit number by a two-digit number

Study the following example –

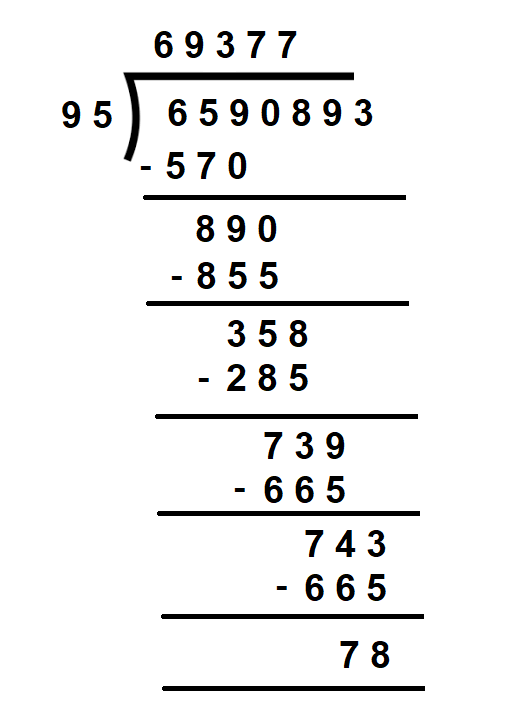
Divide 6590893 by 95

To divide 6590893 by 95, first, take the first digit 9 of the divisor and divide 65 by 9.
9 sevens are 63 but 7 x 95 = 665, which is greater than 659.
So, we take 6 in the quotient and subtract 6 x 95 = 570 from 659.
Now, bring down 0.
Take the first two digits of 890, that is, 89.
Divide by 9. 9 nines are 81 and 9 x 95 = 855.
Subtract 855 from 890. Bring down 8.
Now proceed further in a similar manner till the remainder is less than 95.

Division by 10, 100 and 1000

Division by 10

While dividing a number by 10, the digit at one’s place of the dividend is the remainder and the number formed by the remaining digits of the dividend is the quotient.

This means that if we wish to divide 1567 by 10, the quotient will be 156 and the remainder will be 7.

Therefore, 156 x 10 + 7 = 1567

Similarly, 3297 ÷ 10 will give 329 as the quotient and 7 as the remainder.

We will have, 329 x 10 + 7 = 3297

Division by 100

While dividing a number by 100, the number formed by the first two digits from the right of the dividend is the remainder and the number formed by the remaining digits is the quotient. This means that the digits at the one’s place and the tens place constitute the remainder while the remaining digits form the quotient.

This means that if we wish to divide 32045 by 100, the quotient will be 320 and the remainder will be 45.

Therefore, 320 x 100 + 45 = 32045

Similarly, 100521 ÷ 100 will give 1005 as the quotient and 21 as the remainder.

We will have, 1005 x 100 + 21 = 100521

Division by 1000

While dividing a number by 100, the number formed by the first three digits from the right of the dividend is the remainder and the number formed by the remaining digits is the quotient. This means that the digits at the ones place, tens place, and the thousands place constitute the remainder while the remaining digits form the quotient.

This means that if we wish to divide 165238 by 1000, the quotient will be 165 and the remainder will be 238.

Therefore, 165 x 1000 + 238 = 165238

Similarly, 980654 ÷ 1000 will give 980 as the quotient and 654 as the remainder.

We will have, 980 x 1000 + 654 = 980654

We have seen how to divide a number by 10 100 or 1000. But what if we have multiples of 10 or 100 or 1000 as divisors, do we divide in the same manner or do we alter our steps? Let us find out?

Division by Products of 10

While dividing a number by 20, 30, 40 and so on first divide the dividend by the digit at the tens place of the divisor and then divide the quotient by 10.

For example, let us divide 90 by 30.

We follow the following steps for this division:

1. First we divide 90 by 3. We will get the quotient as 30

2. Now divide 30 by 10, that is we get quotient as 3

Therefore, 90 ÷ 30 = 3

Division by Products of 100

While dividing a number by 200, 300, 400 and so on first divide the dividend by the digit at the hundreds place of the divisor and then divide the quotient by 100.

For example, let us divide 605400 by 200.

We follow the following steps for this division:

1. First we divide 650400 by 2. We will get the quotient as 325200.

2. Now divide 325200 by 100, that is we get quotient as 3252

Therefore, 605400 ÷ 200 = 3252

Properties of Division

Lets get through some of the important properties of division

Division by 1

When we divide a number by 1, we get the number itself.

For example, if we divide 52 by 1, we will get 52 as the quotient.

52 ÷ 1 = 52

Division by 0

It is not possible to divide any number by 0. In other words, we can say that a number divided by 0 is not defined.

Division of 0

When we divide 0 by any number we get 0 as the quotient.

For example, 0 ÷ 4 = 0

Division by the number itself

Any number when divided by itself, will give the quotient as 1.

For example 29 ÷ 29 = 1

Closure Property

Closure property states that when an operation is performed on two numbers, the resultant would also be of the same type as the numbers on whom the operation has been performed.

This means that if you divide one whole number from the other, the quotient would also be a whole number. Let us check whether the closure property holds true for division.

Consider two numbers, 15 and 3.

Divide 15 by 3. We get the quotient as 5, and the remainder as 0, as 3 x 5 = 15. In this case, the quotient is a whole number.

Now divide 26 by 4. We get the quotient as 6.5 and 0 as the remainder. But, 6.5 is not a whole number.

This means that closure property may or may not hold true for division.

Hence we can say that division does not satisfy the closure property.

Commutative Property

Commutative Property states that when an operation is performed on two numbers, the order in which the numbers are placed does not matter. This means that if one number is divided from the other, it does not matter which number is marked as the divisor and which one is the dividend. Does this hold true for division?

Let us find out.

Suppose we have two numbers 10 and 4.

We want to divide 10 from 4. The quotient would be 2.5 and the remainder would be 0.

Now, if we interchange the divisor and the dividend, will we get the same answer? No.

This means that, if we have two numbers, a and b, then

a ÷ b ≠ b ÷ a

Hence, division is not commutative for whole numbers.

Associative Property

Associative Property states that when an operation is performed on more than two numbers, the order in which the numbers are placed does not matter. Since division is not commutative it is al onto associative as well.

Division to find the solution to Everyday Problems

We use division to find solutions to everyday problems, though at times we don’t even recognize it. Suppose we have a total of 488 school students who are to be seated in an auditorium. One row of the auditorium can seat 15 students. How many rows will be fully occupied by the students?

This is a classic example where we use division to find a solution. There are 488 school students and one row can accommodate 15 students. In order to find out how many rows will be required, we need to divide 488 by 15.

By using multiplication tables, we can find out that 32 x 15 = 480. This means that a total of 32 rows of the auditorium will be fully occupied while the remaining 8 students will be seated in another row.

So, there would be 32 fully occupied rows and one row that would be partially occupied.

Division of decimals

Division of decimals is similar to the division of whole numbers, except for the decimal point that needs to be adjusted post division.

Dividing a decimal by 10, 100 1000, etc.

In order to divide a decimal by 10, the decimal point is shifted to the left by one place.

For instance, if we divide 12.68 by10, the result would be 1.268.

In order to divide a decimal by 100, the decimal point is shifted to the left by two places.

For instance, if we divide 1275.7 by100, the result would be 12.757

In order to divide a decimal by 1000, the decimal point is shifted to the left by three places.

For instance, if we divide 32.256 by1000, the result would be 0.032256

Note that if there are no more digits on the left side of the number, we must add 0 to the left as done above.

Dividing a decimal by a whole number

The following steps are involved when dividing a decimal by a whole number

Check the whole number part of the dividend.

If the whole number part of the dividend is less than the divisor, then place a 0 in the ones place in the quotient. Else, move to the next step.

Divide the whole number part of the dividend.

Place the decimal point to the right of the ones place in the quotient obtained in step 1.

Divide the decimal part of the dividend by the divisor. If the digits of the dividend are exhausted, then place zeros to the right of the dividend and remainder each time and continue the process.

Let us understand this by an example.

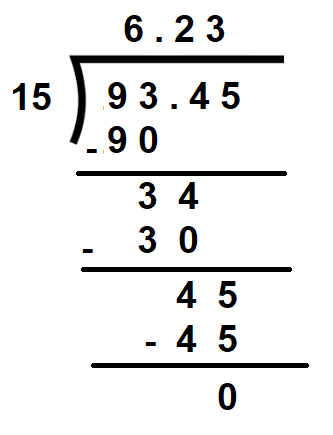
Divide 93.45 by 45

We have,

Dividing a decimal by a decimal

In order to divide a decimal by another decimal, we follow the following steps –

1. Multiply the dividend and the divisor by 10 or 100 or 1000 etc. to convert the divisor into a whole number.

2. Divide the new dividend by the whole number obtained in the previous step.

Let us understand it by an example.

Suppose we want to divide 3.28 by 0.4

We have, 32.8 / 4 = (32.8 / 4) x (10 / 10) = 32.8/4

Now, 32.8 ÷ 4 = 8.2

Recommended Worksheets

Multiplication and Division Problem Solving (Halloween Themed) Math Worksheets
Division of Rational Algebraic Expressions with Same Denominators (Festa Junina Themed) Worksheets
Division of Rational Algebraic Expressions with Different Denominators (Office Themed) Worksheets

Browse All Worksheets

We spend a lot of time researching and compiling the information on this site. If you find this useful in your research, please use the tool below to properly link to or reference Helping with Math as the source. We appreciate your support!