Geometry is a branch of mathematics that primarily deals with the shapes and sizes of objects, their relative position, and the properties of space. It comes from the Ancient Greek words geo- “earth”, and metron “measurement”. Mathematicians often refer to Greek mathematician Euclid as the “Father of Geometry” due to the many postulates and theorems he applied to this branch of Mathematics. In this section, we will examine all the important concepts in Geometry.
In this branch, one can study shapes, sizes, and patterns, and how they are arranged in space. Here we are talking about shapes that are in one, two, and three dimensions.
Objects that have a length are one dimensional, length and width are two dimensional, and length, width, and depth or height are three dimensional.
Point, Line, Plane, and Solid
- Points have position, no dimensions
- A Line is one dimensional (1D)
- A Plane is two dimensional (2D)
- A Solid is three dimensional (3D)

Eg. Point is a no dimensional figure

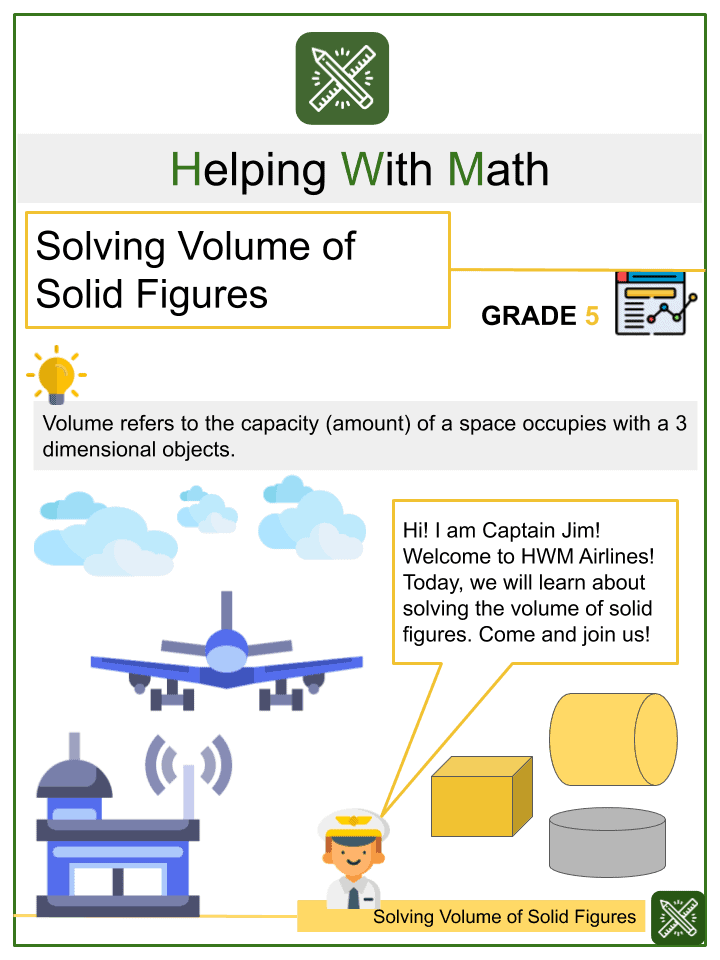
Eg. Line is a one-dimensional figure
Eg. Plane is a two-dimensional figure
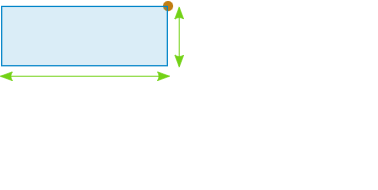
Eg. Solid is a three-dimensional figure
What is Geometry?
The branch of mathematics that deals with distances, angles, patterns, areas, and volumes is known as geometry. Geometry encompasses all the concepts visually and spatially related. It can be classified into three types:
- Euclidean
- Hyperbolic
- Elliptical
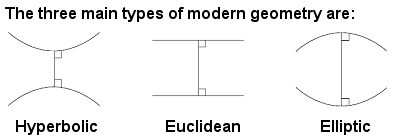
Reference: http://storyofmathematics.lukemastin.com/images2/modern_geometry.gif
Euclidean Geometry
Geometry’s fundamentals can be understood by studying Euclidean geometry. In Euclidean Geometry, plane and solid figures are studied using axioms (a statement or proposition) and theorems. There are several fundamental concepts of Euclidean geometry, such as Points and Lines, Axioms and Postulates, Geometrical Proof, and Euclid’s Fifth Postulate. Euclidean Geometry has five fundamental postulates that define geometrical figures.
- A straight line segment connects any two points.
- A straight line is indefinitely extended in both directions.
- Using any point as the center and any length as the radius, a circle can be drawn.
- All right angles are congruent.
- Any two straight lines that are equidistant from one another at two points are infinitely parallel.
Euclid’s Axioms
An axiom or postulate is based on assumptions without any supporting proof. There are a few axioms of geometry that are universally accepted by everyone.
- All things that are equal to each other are equal. If A = C and B = C then A = C
- When equals are added together, the whole is equal. If A = B and C = D, then A + C = B + D
- When equals are subtracted, the remainder is equal.
- Coinciding things are equal to one another.
- There is greater value in the whole than in its parts. If A > B, then there exists C such that A = B + C.
- Things that are double the same are equal to one another.
- Half of the same thing is equal to the other.
Non-Euclidean Geometry
The non-Euclidean geometries are spherical and hyperbolic. In comparison to Euclidean geometry, non-Euclidean geometry differs in how it views parallel lines and angles in planar space.
- Spherical geometry entails the study of geometric planes on a sphere. A line is the shortest path between two points along it. This line on a sphere is an arc and is known as the great circle. The sum of the angles in the triangle is greater than 180º.
- A hyperbolic surface is a curved surface. In topology, this geometry finds application. A planar triangle has a sum of angles less than 180º depending on the inner curvature of the curved surface.
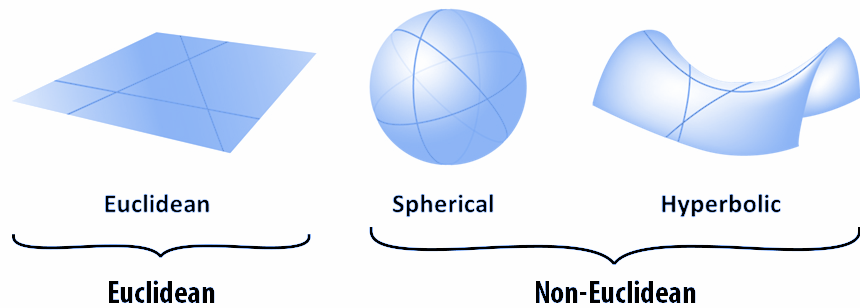
Plane Geometry
Euclidean geometry is the study of geometry on a plane. Essentially, a plane is a two-dimensional surface that extends endlessly in both directions. Geometry and graph theory relies heavily on planes. The basic components that constitute planes in geometry are analogous to points, lines, and angles. In geometry, a point represents the basic no-dimensional unit. They are called collinear points if they lie on the same line.
- A line is a unidimensional unit that represents a set of points in two opposite directions.
- Lines are thought of as intersections of two planes.
- There are no endpoints on a line.
- A line, a line segment, and a ray are easily distinguished.
- Lines can be parallel or perpendicular.
- The lines may or may not intersect.
Angles in Geometry
Angles are formed when two straight lines or rays intersect at a point. Angles are typically measured in degrees. Angles can be acute, obtuse, right angled, straight angled, or obtuse. Angle pairs can be supplementary or complementary. It is an intricate component of geometry to construct angles and lines. The study of angles in a unit circle and in a triangle forms the basis of trigonometry. The parallel lines and their theorems can be viewed in more detail by examining the transversals and related angles.

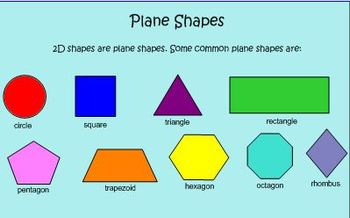
Plane Shapes in Geometry
We can identify and classify plane shapes based on their properties. Geometric shapes of the plane are flat shapes or two-dimensional shapes. A polygon is a closed curve with more than two lines. Triangles are closed figures with three sides and three vertices. Triangles have many theorems arising from their properties. There are several important theorems in geometry based on triangles, including Heron’s formula, The Exterior Angle Theorem, Angle Sum, Basic Proportionality, Similarity and Congruence, Pythagoras Theorem, etc. We can use these to recognize angles and sides in triangles. Polygons with four sides and four vertices are called quadrilaterals. Circles do not have edges or corners, and they are closed figures. Circles are defined as being equidistant from a given point called the center. The formative chapters of geometry are centered on symmetry, shape transformations, and shape construction.
Solid Geometry
Geometric solid shapes are three-dimensional. The dimensions that are considered: length, width, and height. Figures like cylinders, cubes, spheres, cones, cuboids, prisms, pyramids, and so on are solid figures that take up space. Vertices, faces, and edges characterize them. The five platonic solids and polyhedra have interesting properties in Euclidean space. The nets of plane shapes can be folded to form solids.
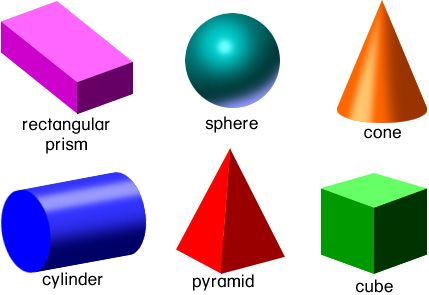
Reference: https://in.pinterest.com/pin/25473554112096788/
Measurement in Geometry
Measurement in geometry involves the calculation of length or distance, the area of a flat shape, and the volume of solid objects. Geometric measurements are used to compute the perimeter, area, capacity, surface area, and volume of geometric figures. A solid’s volume is the amount of area it occupies, and its surface area is the sum of its faces. The perimeter of a solid is the distance around it, the area is the region it occupies, and the area of its area is the sum of its areas.
Two-dimensional Analytical Geometry
The concept of analytical geometry is the study of the position of any given point on a plane in terms of a rectangular Cartesian coordinate system using ordered pairs of numbers, or coordinates. A coordinate axis divides a plane into four quadrants. In order to visualize the geometric objects on the coordinate plane, identifying and plotting points will be necessary. In the example below, the point is defined as (4,2).
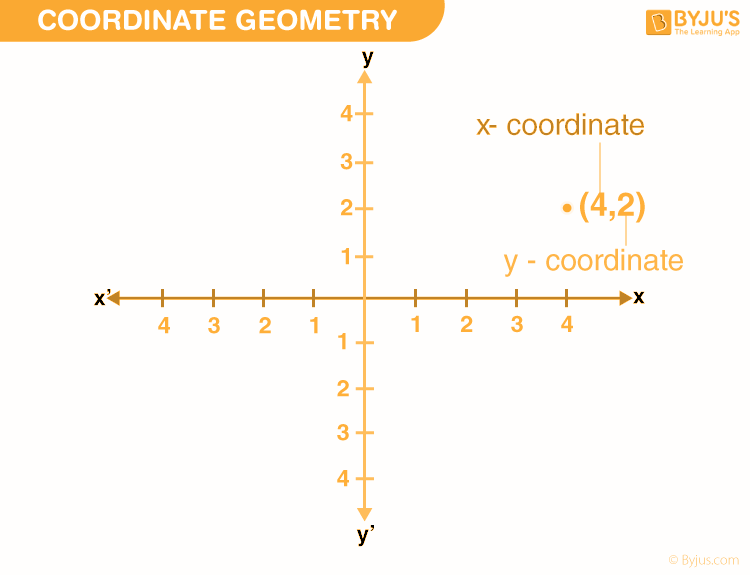
Reference: https://cdn1.byjus.com/wp-content/uploads/2020/02/Coordinate-Geometry-1.png
The properties of geometric figures, such as straight lines, curves, parabolas, ellipses, hyperbolas, circles, and so on, can be studied through coordinate geometry.
By visualizing algebraic equations as curves in analytical geometry, the mathematical concepts of algebraic equations are better understood. We can determine the distance formula, the section formula, the midpoint formula, the centroid of a triangle, the area of a triangle formed by three given points, and the area of the quadrilateral formed by four points using the known coordinates in the cartesian coordinate system. Using analytical geometry, the equation of a straight line passing through a point, or two points, and the angle between two straight lines can be easily calculated.
Three-dimensional Geometry
Three-dimensional geometry deals with the geometry of shapes in 3D space in the cartesian planes. Every point in the space is denoted by 3 coordinates, expressed as an ordered triple (x, y, z) of real numbers.
Direction Cosines of a Line
If a straight line forms angles α, β and γ with the x-axis, y-axis, and z-axis respectively then cosα, cosβ, cosγ are known as the direction cosines of a line. These are denoted as l = cosα, m = cosβ, and n = cosγ. For l, m, and n, l2 + m2 + n2 = 1, where the direction cosines of a line joining the points P(x1, y1, z1) and Q(x2, y2, z2) are given as x2 – x1 / PQ , y2 – y1 / PQ , z2 – z1 / PQ where PQ = √ (x2 – x1) + (y2 – y1) + (z2 – z1)
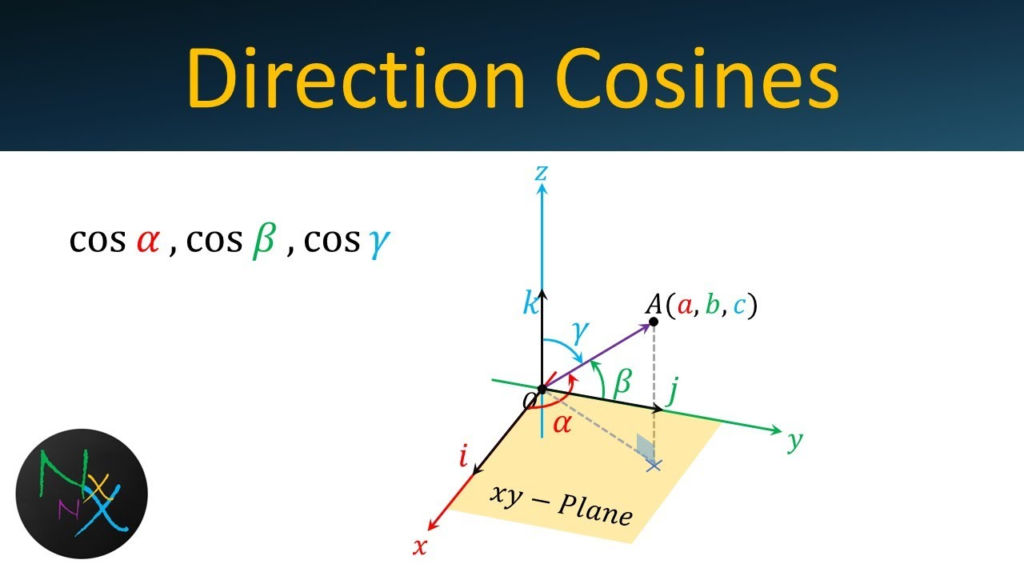
cosα, cosβ, cosγ
Reference: https://i.ytimg.com/vi/BlzOoZsK0EU/maxresdefault.jpg
Direction Ratios of a Line
A line’s directional ratio is a number that is proportional to the direct cosines of the line. If l, m, n are the direction cosines, and a, b, c are the direction ratios, then
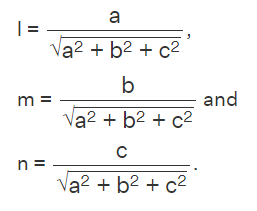
The directions ratio of the line joining the points P(x1, y1, z1) and Q(x2, y2, z2) are
(x2 – x1) , (y2 – y1) , (z2 – z1) or (x1 – x2) , (y1 – y2) , (z1 – z2)
Skew lines in Geometry
A skew line is a line that is neither parallel nor intersecting, and that lies in a different plane. The angle between two lines is cos θ = | l1l2 + m1m2 + n1n2 | where θ represents the acute angle between the lines. Also,
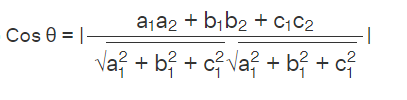
Equation of Line in 3-D Geometry
- Vector equation of the line passing through a point having the position vector a→ parallel to vector b→ is r→ = a→ + λb→
- Cartesian equation of the line that is passing through the point (x1, y1, z1) and direction cosines l, m, n is
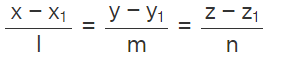
- Vector equation of the line passing through two points with the position vectors a→ and b→ is r→ = a→ + λ(b→ – a→)
- Cartesian equation of the line that is passing through the point (x1, y1, z1) and (x2, y2, z2) is
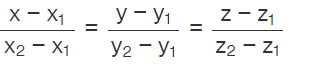
Angle Between Two Lines
The angle between intersecting lines that are parallel to the skew lines is the angle between skew lines. If θ is the angle between r→ = a→1 + λb→1 and r→ = a→2 + λb→2 , then
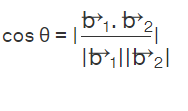
Examples of Geometry
Example 1:
Given ABC and ADE are two triangles that are similar. Find the length of BC if AD = 7 units, DB = 3 units, AE = 4 units and DE = 7 units.
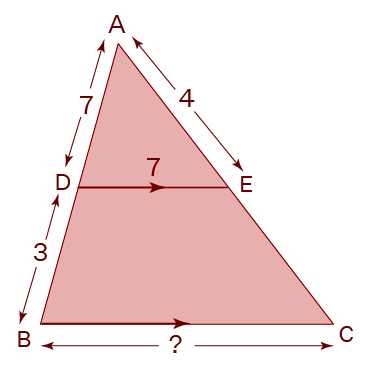
Solution: In geometry, similar triangles have the same proportion.
As you can see that the given triangles, ABC and ADE are similar.
Thus, AB/ AD = AC / AE = BC/ DE
To find: BC
Given: AB , AD, DB, DE and AE.
AB = AD + DB = 7 + 3 = 10 units
We know that AB/ AD = BC/ DE
10/7 = BC/7
70/7 = BC
BC = 10 units
Answer: The missing side BC = 10 units
Example 2:
Find the direction cosines of the z-axis.
Solution: In 3-dimensional geometry, if a straight line makes angles α, β and γ with the x-axis, y-axis, and z-axis respectively then cosα, cosβ, cosγ are called the direction cosines of a line.
The z-axis makes 90º, 90º, and 0º with x, y, and z axes respectively.
Thus their cosines are cos 90º, cos 90º, and cos 0º
cos 90º = 0, cos 0º = 1.
Therefore the direction cosines are 0,0,1
Answer: The direction cosines of the z-axis are 0,0,1.
Example 3:
Is a cone a 2-D or a 3-Dl shape?
Answer: A cone is a 3-D solid shape with a circular base and a single vertex. The surface of the cone is narrowed from the base to the vertex.
Subfields of Geometry
The study of geometry today is divided into many subfields. We describe only a few of them here:
Riemannian geometry
This involves the study of manifolds that are equipped with the additional structure of a Riemannian metric, a rule for measuring curve lengths and angles between tangent vectors. A Riemannian manifold has curvature, and it is specifically this curvature that makes up the laws of classical Euclidean geometry that is usually taught in elementary school, to be different. For instance, the sum of interior angles of a “triangle” on a curved Riemannian manifold will be more or less than π if the curvature is positive or negative, respectively.
Algebraic geometry
It is the study of algebraic varieties, which are a set of solutions to polynomial equations. Sometimes they are manifolds, but they can also have “singular points” where they are not smooth. They can be studied much better in terms of abstract algebra because they are defined algebraically, and many questions in pure algebra can be understood better when the problem is reformulated in terms of algebraic geometry. Further, one can study varieties across various fields, not just real or complex numbers.
Symplectic geometry
Symplectic forms are manifolds with an added structure. In a sense (that can be made precise) a symplectic form is the opposite of a Riemannian metric, and symplectic manifolds behave quite differently from Riemannian manifolds. As an example, Darboux’s famous theorem states that symplectic manifolds are all “locally” the same, despite being highly different globally. Theorems like these are not true in Riemannian geometry. From classical mechanics, symplectic manifolds emerge as natural properties of physical systems. They are also known as phase spaces in physics. This branch of geometry is highly topological in nature.
Complex geometry
A study of manifolds that appear to be n-dimensional spaces but are modeled on ]complex numbers as opposed to real numbers. Holomorphic (or complex-analytic) functions are more rigidly defined than the real case (for example, not all smooth functions are real-analytic), so there are fewer types of complex manifolds. At least partially these types have been classified. Algebraic geometry is also closely related to this field.
How Is Geometry Used?
Geometry is used daily by almost everyone, even without ever studying geometry. When you get out of bed in the morning or parallel park your car, your brain makes geometric spatial calculations. Geometry explores spatial sense and geometric reasoning.
Besides art and architecture, geometry can also be found in robotics, astronomy, sculptures, nature, sports, machines, and cars, and many such fields.
Geometry tools typically include compass, protractor, square, graphing calculator, Geometer’s Sketchpad, and rulers.
This branch of mathematics deals with the study of every shape and figure in the universe as well as all its mathematical principles. Plants, animals, microbes, and our everyday lives are examples of this. It is a world of shapes and geometry teaches us how to unravel its mysteries.
References:
- https://www.britannica.com/science/geometry
- http://spintronicbbsr.org/lecturer_notes/3D-7.pdf
- https://www.mathsisfun.com/geometry/dimensions.html
- https://www.skillsyouneed.com/num/geometry.html
- https://www.thoughtco.com/what-is-geometry-2312332
- https://www.splashlearn.com/math-vocabulary/geometry/geometry#:~:text=Different%20shapes%20in%20geometry%20have,interior%20angles%20is%20360%CB%9A
Recommended Worksheets
Geometry and Measurement Problem Solving (World Space Week Themed) Math Worksheets
Circumference of a Circle (Summer Party Themed) Worksheets
Solving Word Problems Involving Volume of Cylinders, Cones, and Spheres 8th Grade Math Worksheets