Introduction
In this article, we learn all about triangles. Starting with the definition and properties of the shape, we learn through intuitive backgrounds before we finally measure the dimensions of the shape through its sides and how much area a triangle takes. While doing so, we will also try some examples to guide us in learning.
What is a Triangle?
A triangle, by definition, is a shape that has three sides. When we think of a triangle, we can associate it with road signs, pyramids, flags, and even musical instruments!
In geometric terms, a triangle consists of a set of three straight lines or sides, three interior angles that are formed by the sides, and three vertices that are intersections of the lines forming the triangle.
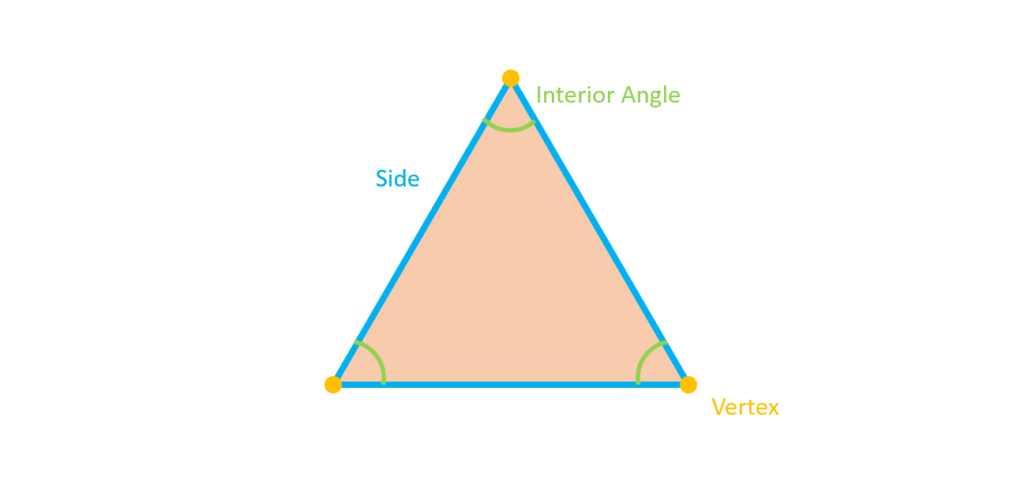
What are the Types of Triangles?
We mostly recognize triangles as having three sides. But what are the specific types that a triangle can take, and how can we differentiate them? Apparently, triangles can be described based on either the characteristics of their sides or their interior angles.
Based on Side Length
Triangles can be classified according to the length of their sides. They can either be an equilateral triangle, an isosceles triangle, or a scalene triangle.
An equilateral triangle is a triangle wherein all sides have equal length.
On the other hand, an isosceles triangle is a triangle with two sides of equal length.
If a triangle has all sides with different lengths, it is said to be a scalene triangle.
Based on Interior Angles
Triangles can also be classified based on the measure of their interior angles. There are three types according to the interior angles of a triangle: acute triangles, oblique triangles, and right triangles.
An acute triangle is a triangle whose two interior angles measure less than 90°.
On the other hand, an oblique triangle is a triangle with one interior angle measuring less than 90°.
Then, a right triangle is a triangle with one interior angle measuring exactly 90°.
What is a Perimeter?
We define the perimeter of a two-dimensional shape as a measure of the boundary enclosing it.
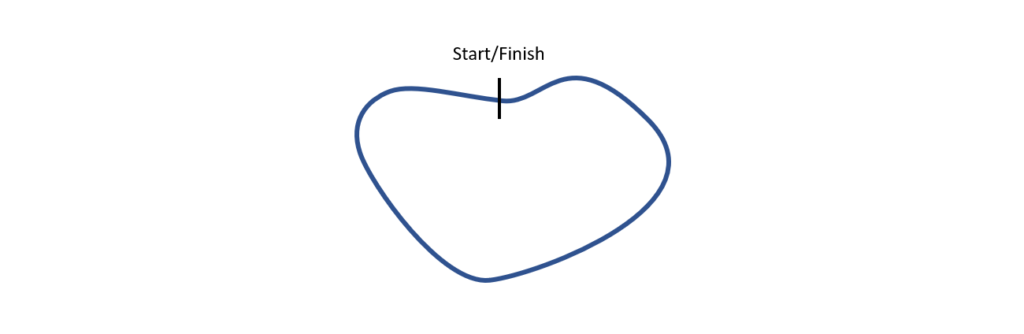
In an intuitive approach, we can relate the idea of a perimeter to how far we jog through a lap in the park. If we begin measuring the distance from the start of the lap, and then trace a closed path until we get back to the starting point, we can measure the perimeter of the park through the lap we have run across:
Thus, for any closed shape we can get its perimeter by taking the length of the edges enclosing the shape.
What is an Area?
On the other hand, we can define the area of a two-dimensional shape as a measure of the space it occupies in the two-dimensional plane.
Intuitively, we can think of shapes in a plane as objects in a room. Each object takes up some space in the room, depending on the kind of object and its size. In this sense, we can measure a shape’s area through the shape’s dimensions.
Perimeter of a Triangle
From the definitions provided earlier, we can now discuss in detail the formula for solving the perimeter of a triangle. We first derive the basic formula involved, provide intuitive insights, and then show how we apply this formula with some examples.
Derivation of the Perimeter Formula of a Triangle
We know that the perimeter can be defined as the sum of the lengths of all edges covering a shape. In a triangle, we have three edges. Hence, we can say that the perimeter of a triangle can be expressed as the sum of the length of each side of the triangle:
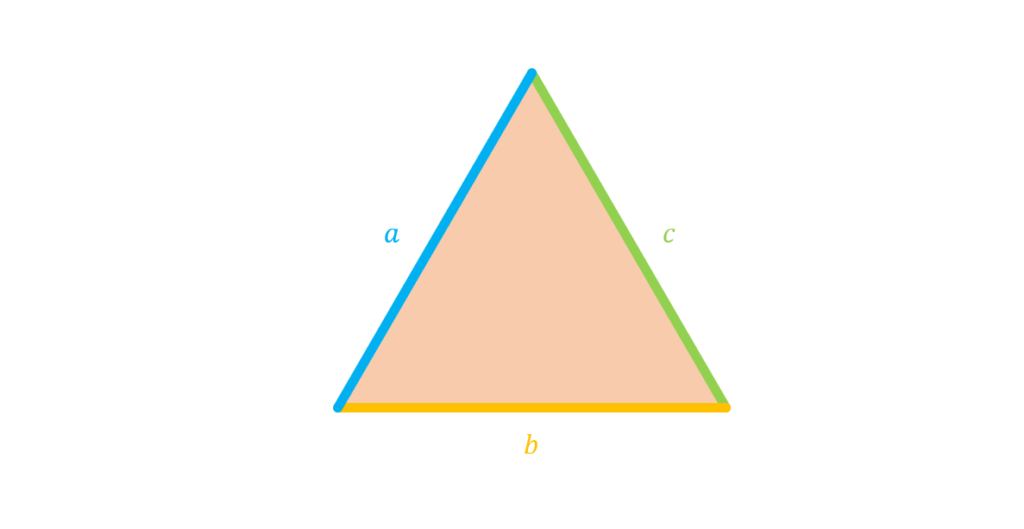
Perimeter=Length of 1st Side+Length of 2nd Side+Length of 3rd Side
If we denote each side as a, b, and c, we can compress this formula into a shorter form:
Perimeter=a+b+c
What is the Perimeter Formula of a Triangle?
From the previous derivation performed, the perimeter P of a triangle whose sides a, b, c are known is given by:
P=a+b+c
We note that the unit of the perimeter is expressed in terms of the same units as with the sides given.
How is it Used?
As a practice on how to apply the formula, let us work together on finding the perimeter of the triangle shown below:
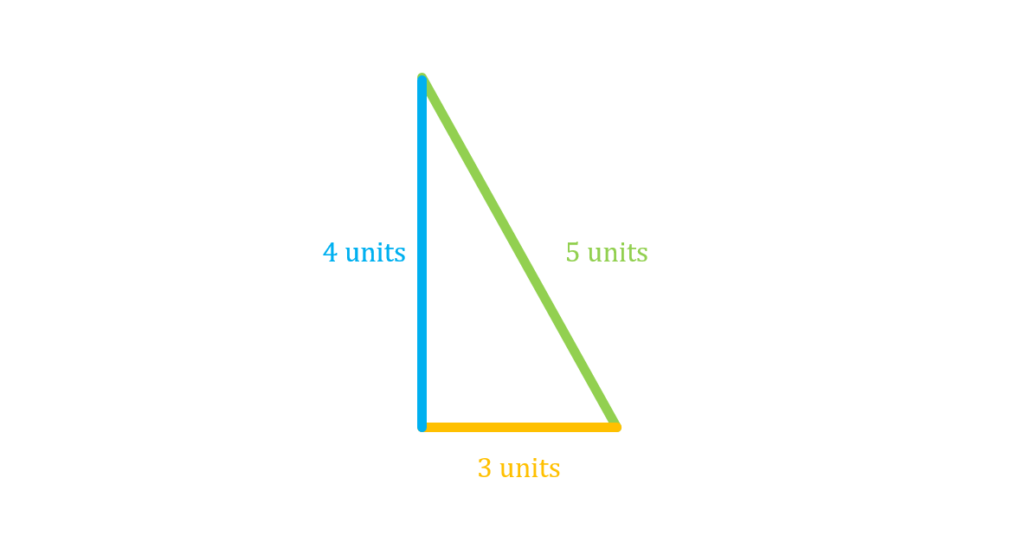
From the given figure, we set the order of the sides arbitrarily and assign the given values to each side. Hence, we can say that:
a=4 units
b=3 units
c=5 units
Moreover, since the lengths of all sides are known, we can use the Perimeter Formula for a triangle:
P=a+b+c
We then substitute the given lengths to the formula to get:
P=4 units+3 units+5 units
Afterward, we add the numbers to obtain the value of the perimeter:
P=12 units
We then conclude that the perimeter of the triangle is 12 units. This quantity is expressed in terms of the same units as the radius.
Area of a Triangle
After learning about the Perimeter Formula of a triangle, we can furthermore measure the area of a triangle based on the dimensions of the said shape.
Derivation of the Area Formula of a Triangle
We first consider one side of a triangle, preferably its longest side. We call this side the base of the triangle:
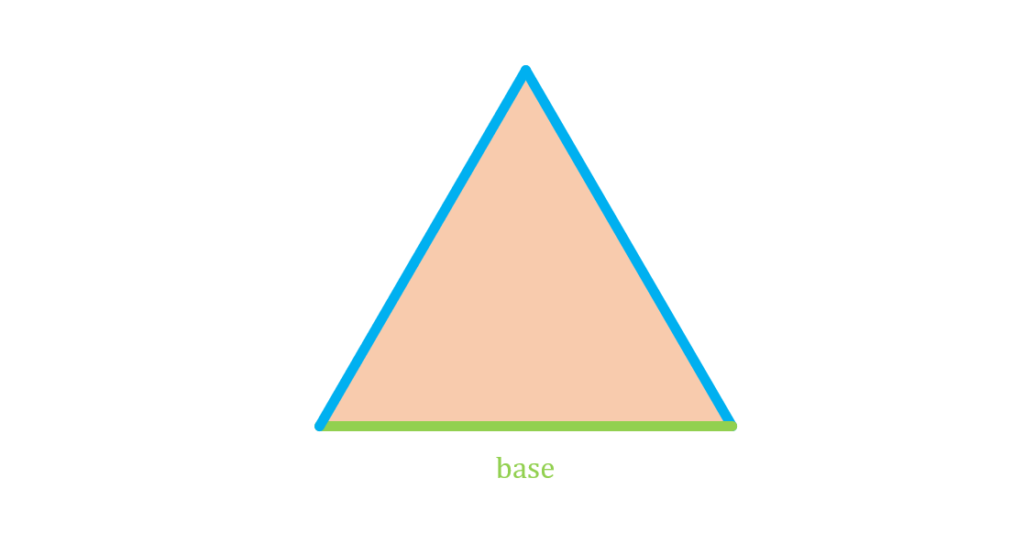
Then, we form a line that is perpendicular to this side and passes through one of the vertices of the triangle. This is called the altitude of the triangle:
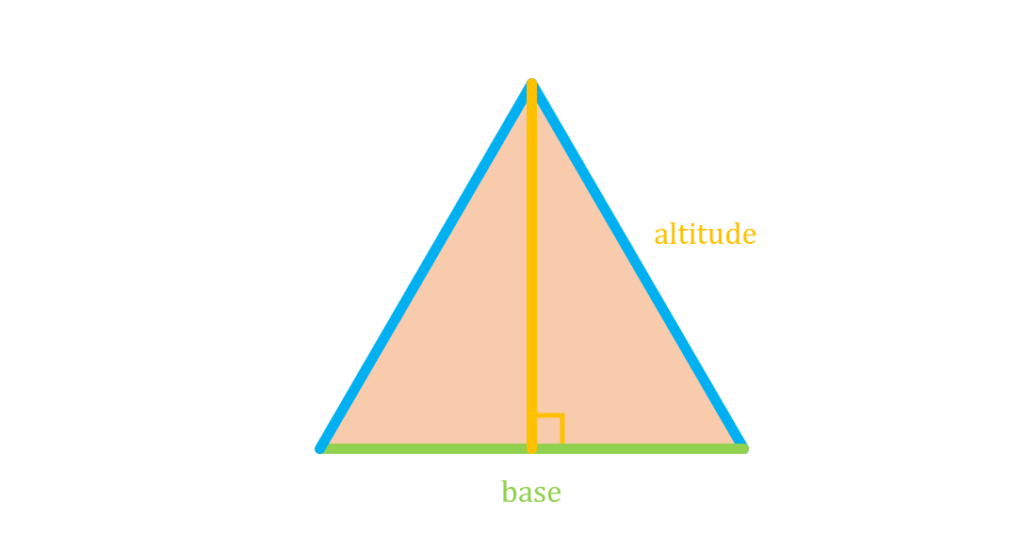
If we reimagine the triangle as a right triangle whose sides are given by the base and the altitude, we have the following figure:
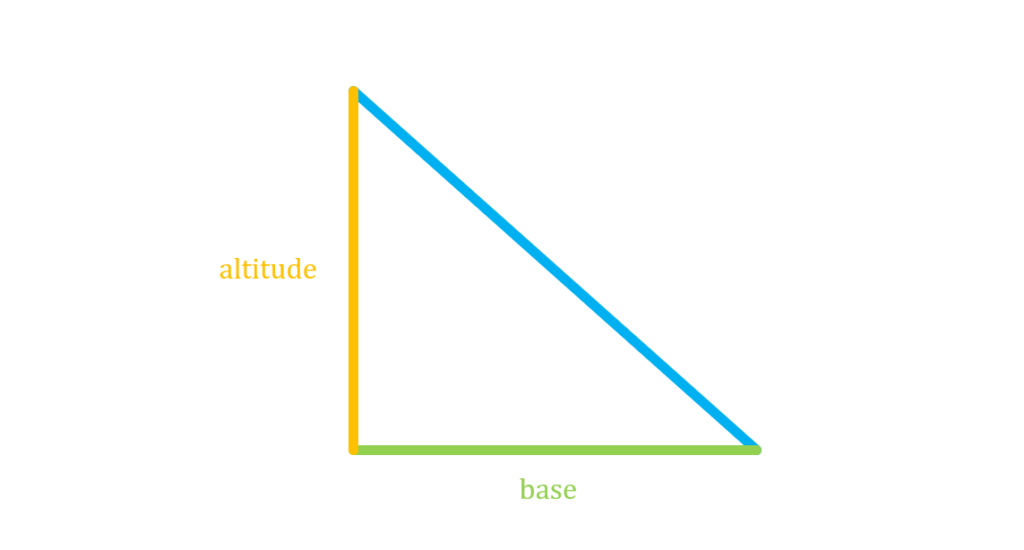
Now, suppose we superimpose a rectangle whose length is equal to the base of the triangle, and whose height is equal to the altitude of the triangle:
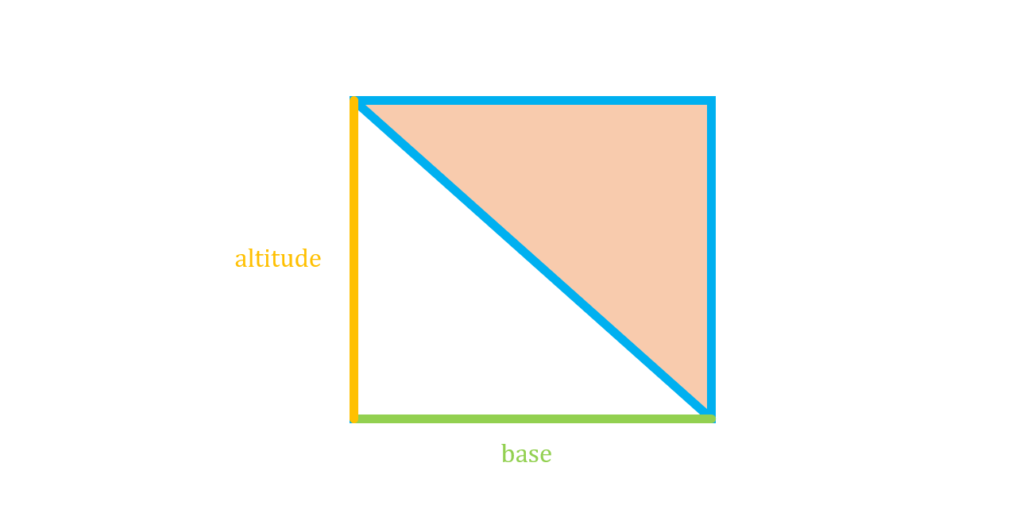
From the Area Formula of a rectangle, we know that the area of this rectangle is given by:
Arectangle=base×altitude
Upon observation, we see that the reimagined triangle has an area that is half the area of the superimposed rectangle. Hence, we can say that:
Area=½ x Arectangle
If we substitute the Area Formula for the rectangle, we then arrive at the Area Formula for a triangle:
Area=½ x base x altitude
What is the Area Formula of a Triangle?
Through the derivation we have previously done, the area A of a triangle whose base b and altitude h is known can be expressed using the formula:
A=½bh
We note that for both formulas, the unit of the area is expressed in terms of squared units of the given radius/diameter.
How is it Used?
Again, we practice what we have learned so far by working on a guided example for finding the area of the triangle:
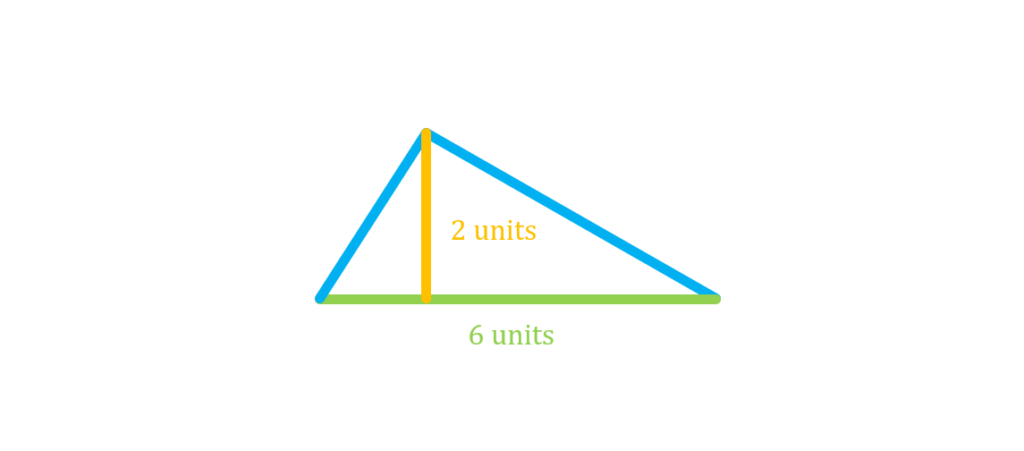
From the given figure, we are given the base of the triangle to be 6 units, and its altitude to be 2 units. Hence, we can say that:
b=6 units
h=2 units
Moreover, since the base and altitude are known, we can use the Area Formula of a triangle:
A=½ bh
We then substitute the given base and altitude to the formula, and we get:
A=½ x 6 units × 2 units
Afterward, we multiply the numbers together to obtain the area of the triangle:
A=6 units2
We then conclude that the area of the triangle is 6 units2. This quantity is expressed in terms of squared units of the radius.
Problem-Solving Examples
We can now proceed to solve sample problems to apply what we have learned so far. Each problem tackles different formulas discussed and gives us a challenge on how to solve through the information given to us.
Perimeter of a Triangle
Sample Problem 1:
What is the perimeter of an isosceles triangular glass pane whose sides are given 4 cm 4 cm, and 3 cm?
Solution:
We recall that the perimeter P of a triangle is given by the formula:
P=a+b+c
With the given side lengths a=b=4 cm and c=3 cm, we substitute these values into the formula:
P=4 cm+4 cm+3 cm
Finally, by adding the lengths we obtain the value of the perimeter to be:
P=11 cm
Therefore, we conclude that the perimeter of the triangular glass pane is 11 cm.
Sample Problem 2:
An athlete is training for her triathlon. In a triangular lap, she runs for twelve kilometers, swims for five kilometers, then races through thirteen kilometers by bike. How much distance does she train through a single lap?
Solution:
We can first assign the sides of the triangular lap with each part of the triathlon. For this problem, we use the following values:
a=12 km
b=5 km
c=13 km
Then, the perimeter P of a triangle is given by the formula:
P=a+b+c
Hence, we can substitute the given values to get:
P=12 km+5 km+13 km
Lastly, we take the sum of the sides to determine the perimeter of the lap:
P=30 km
Therefore, we conclude that the athlete trains for is 30 kilometers.
Sample Problem 3:
Suppose we have a triangle whose third side is unknown. The lengths of the two sides are given by a=10 in and b=15 in. We are then asked the following:
- What is the length of the third side?
- What type of triangle is formed by the three sides?
- What is the perimeter of the triangle?
Solution:
- For this problem, we are given two sides and an unknown third side. By the Pythagorean Theorem, we can solve for the length of the unknown side c using the given sides a and b:
c=$\sqrt{a^2+b^2}$
Substituting the given lengths, we have:
c=$\sqrt{{10 in}^2+ (15 in)^2}$
Taking the square of both terms inside the radical sign, we expand the sum we wish to solve:
c=$\sqrt{100 in^2+225 in^2}$
Adding the two numbers inside the radical, we simplify the expression into:
c=$\sqrt{325 in^2}$
Finally, we take the square root of the number inside the radical to get the length of the unknown side, then round it off to the nearest whole number:
c=18 in
Therefore, the length of the third side is 18 inches.
- Since each side has a different length, we conclude that the triangle formed by these sides is a scalene triangle.
- We recall that the Perimeter Formula for a triangle is given by:
P=a+b+c
Using the given side lengths a=10 in and b=15 in, along with the computed length of the third side c=18 in, we substitute these values into the equation to get:
P=10 in+15 in+18 in
Adding together these numbers, we then obtain the value of the perimeter:
P=43 in
Therefore, we conclude that the perimeter of the triangle is 43 inches.
Area of a Triangle
Sample Problem 4:
What is the area of a right triangle whose base is 10 units and has an altitude of 18 units?
Solution:
We recall that the area A of a triangle is given by the formula:
A=½bh
With the given base b=10 u, and an altitude of h=18 u, we substitute these into the formula to get:
A=½ x 10 units x 18 units
Finally, by multiplying the three numbers we can compute the value of the area:
A=90 units2
Hence, the area of the right triangle is 90 squared units.
Sample Problem 5:
In the figure below, we are given an isosceles triangle whose sides are shown:
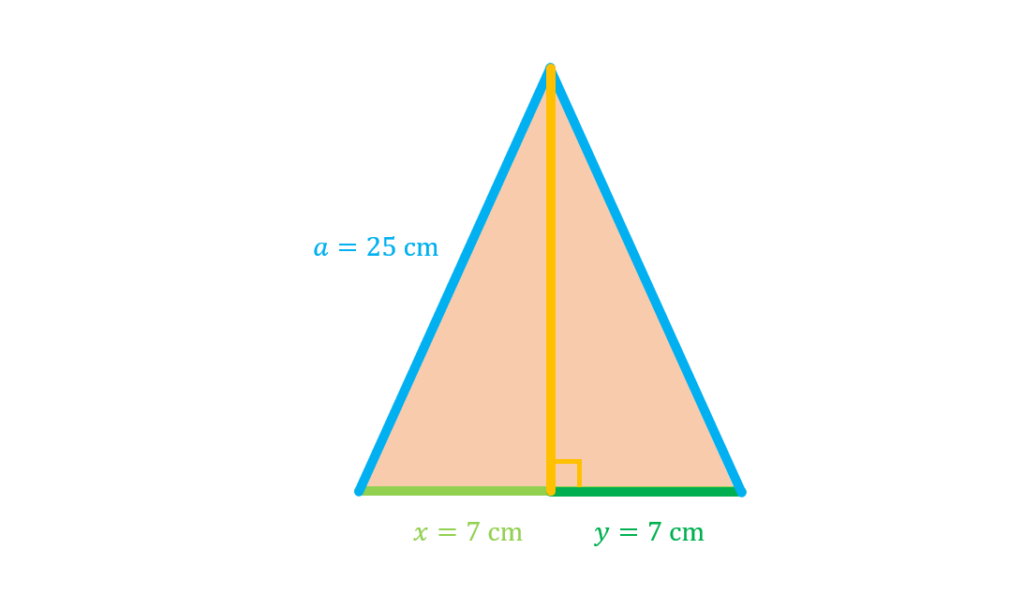
- What is the length of the base of the triangle?
- What is the length of the altitude of the triangle?
- What is the area of the triangle?
Solution:
- We first observe that in the given figure, the base of the triangle can be expressed as the sum of the lengths of x and y:
b=x+y
Substituting the given side lengths x=y=7 cm, we get the value of b:
b=7 cm+7 cm=14 cm
Therefore, the length of the base is 14 cm.
- We note that the altitude forms two right triangles. To solve for the length of the altitude, we apply the Pythagorean Theorem, using the sides a, x, and the altitude h:
a2=x2+h2
Re-writing the equation in terms of the altitude, we have:
h=$\sqrt{a^2-x^2}$
Then, we proceed by substituting the known lengths:
h=$\sqrt{(25 cm)^2-(7 cm)^2}$
Taking the squares of both numbers inside the radical, we get:
h=$\sqrt{625 cm^2-49 cm^2}$
Afterward, we take the difference between the two squares:
h=$\sqrt{576 cm^2}$
Thus, the value of the unknown h can be obtained by taking the square root of the difference obtained earlier:
h=24 cm
Therefore, the length of the altitude of the triangle is 24 cm.
- We recall that the Area Formula for a triangle is given by:
A=½bh
Using the values obtained from Part A and Part B, we know the base and the altitude of the triangle to be:
b=14 cm
h=24 cm
Substituting these values into the formula, we get:
A=½×14 cm×24 cm
Finally, multiplying the numbers together we get the value of the area:
A=168 cm2
Therefore, we conclude that the area of the isosceles triangle is 168 cm2.
Sample Problem 6:
Suppose a painter wants to paint a solid red triangle covering half of a 15 ft×15 ft square wall. For every liter of paint, an area of 100 square feet can be painted. How much red paint does the painter need to finish painting the triangle?
Solution:
We first note that the painter is tasked to paint a right isosceles triangle with red paint. Therefore, we know that the base and the altitude of the triangle are both equal to the length of the side of the square wall:
b=h=15 ft
Then, we solve for the area of the triangle to be painted. Using the Area Formula of a triangle, we have:
A=½bh
Substituting the values we have obtained earlier, we get the product of three numbers:
A=½×15 ft×15 ft
As such, the area of the triangle can be obtained:
A=112.5 ft2
To determine how much red paint the painter needs, we apply the given ratio of 1 liter :100 ft2, as shown below:
1 l=100 ft2
For an area A=112.5 ft2, the amount of red paint R required is given by:
R=112.5 ft2 x ($\frac{1l}{100 ft^2}$)=1.125 liters
Therefore, the painter needs 1.125 liters of red paint to finish painting the red triangle.
Summary
A triangle is a shape that has three sides. It is also formed by a set of three interior angles, formed between the sides of the triangle, and three vertices, or intersections of the sides of the triangle.
A triangle can be classified according to the following characteristics:
Based on side length: an equilateral triangle has all sides equal, an isosceles triangle has two equal sides, and a scalene triangle has no equal sides,
Based on interior angle measure: an acute triangle has two interior angles measuring less than 90°, an oblique triangle has one interior angle measuring less than 90°, and a right triangle has one angle measuring exactly 90°.
A perimeter is a measure of the boundary enclosing a shape. It can be obtained by taking the length of the edges enclosing the shape.
On the other hand, an area is a measure of the space a shape occupies in a 2D plane. This quantity is dependent on the dimensions of the shape.
The perimeter P of a triangle with known sides a, b, c is given by the following formula:
P=a+b+c
The area A of a triangle whose base b and altitude h is known can be determined using the formula:
A=½bh
Recommended Worksheets
Triangles (Fashion Themed) Worksheets
Perimeter of a Triangle (Thanksgiving Themed) Math Worksheets
Area of Triangles (Ice cream Themed) Worksheets









