Supplementary Angles

Introduction

In geometry, different names are given to different angels and their combinations depending upon the type of angles they make. For example, an angle may be a right angle, an acute angle or an obtuse angle, depending upon the angle it makes with a straight line. Similarly, a pair of angles can be complementary angles or supplementary angles depending upon their sum. Depending upon the placement of the angles, there may be adjacent angles, opposite angles, corresponding angles, alternate angles and so on. One of the important terms in geometry is supplementary angles. Let us understand what supplementary angles are all about.

 Before we look into the concept of supplementary angles, let us first understand the meaning of the term supplementary. Where did this term supplementary come from?

The Origin of the word Supplementary

The word “supplementary” has been derived from two Latin words “Supplere” and “Plere”. Here, the word “Supplere” means “supply”, while the meaning of the word “Plere” is “fill”. Therefore, the combination of these two words means “something when supplied to complete a thing”. So, how do we define supplementary angles? Let us find out.

What are Supplementary angles?

Two angles are said to be supplementary if their sum is 180^o. For example, two angles, 130^o and 50^o are supplementary because their sum, 130^o + 50^o = 180^o. Together, the supplementary angles form a straight line.

When the sum of two angles is 180^o, i.e. when two angles are supplementary angles, they are said to be supplements of each other. This means that the angles, 130^o and 50^o, since their sum are 180^o, therefore the angle 130^o is the supplement of 50^o and vice versa.

Before moving ahead with the concept of supplementary angles, it is important to recall two other important concepts in geometry, namely, straight line and adjacent angles.

Let us recall what do we mean by a straight line and what does it form?

A straight line is an infinite length line that does not have any curves on it. The angle formed by a straight line is always equal to 180^o

For example, let us consider the below figure

Here the line AB forms a straight line. Since the angle formed by a straight line is always equal to 180^o, therefore, ∠ x + ∠ y = 180^o

Now, let us recall what do we mean by adjacent angle?

Two angles are said to be adjacent if they have a) a common vertex b) a common arm and c) the other two arms are on opposite sides of the common arm, i.e. they must not overlap each other.

For example,

Here x and y are non-adjacent angles

In the above figure, ∠ 1 and ∠ 2 are adjacent angles.

It is very important to learn about adjacent angles and straight lines in order to understand supplementary angles properly. Let us see why?

Adjacent Angles and Supplementary Angles

We have now read that two angles are said to be supplementary if their sum is 180^o. Now, this can happen in two ways:

• Supplementary angles are adjacent angles
• Supplementary are non-adjacent angles

Adjacent Supplementary angles

We know that adjacent angles have a common vertex, common arm, the other two arms are on opposite sides of the common arm, i.e. they must not overlap each other. Now if the sum of these adjacent angles is 180o, they are said to be supplementary angles. Such angles are called a linear pair of angles

Let us understand this through an example.

Suppose we have a straight line AB. A slant line CD passes through the line AB, making an angle of 60^o on one side and 120^o on the other side, as shown in the figure below:

Now, we can see that ∠ ACD and ∠ BCD are adjacent angles. Also the sum of ∠ ACD and ∠ BCD = 120^o + 60^o = 180^o

Therefore, the angles ∠ ACD and ∠ BCD are adjacent as well as supplementary.

Note the sum of these two angles is 180o, as they fall on a straight line and we know that the angle of a straight line is 180^o

Non-Adjacent Supplementary angles

Non-adjacent supplementary angles are the angles that are a supplement to each other but are not adjacent, i.e. do not share a common vertex or an arm. Let us understand this through an example.

Suppose, we have two angles, as shown in the figure below:

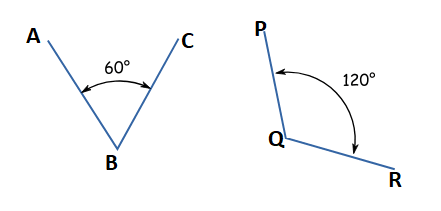
In the above figure, we can see that ∠ ABC = 60^o while ∠ PQR = 120^o

Now, if we sum up these two angles, i.e. if we find ∠ ABC + ∠ PQR, we will see that

 ∠ ABC + ∠ PQR = 180^o

Therefore, the angles ∠ ABC and ∠ PQR are supplementary angles. However, it may also be noted that these two angles are not adjacent angles. Therefore, we can say that there may be a pair of supplementary angles that are not adjacent to each other.

Similar to supplementary angles, a common term used in geometry are complementary angles. But are Supplementary angles and Complementary angles the same or do they differ from each other? Let us find out.

Complementary Angles

Complementary angles are the pair of angles that have the sum of 90^o. For instance, if we have a pair of angles, say 60^o and 30^o, we can say that these two angles are complementary as 60^o + 30^o = 90^o. Other properties of complementary angles are similar to that of supplementary angles such as:

1. The pair of complementary angles are called as each other’s complement.
2. Complementary angles can be a pair of adjacent as well as non-adjacent angles.

The major differences between the Supplementary angles and the Complementary angles can be summarised as:

Supplementary Angles	Complementary Angles
The sum of the pair of supplementary angles is equal to 180o	The sum of the pair of complementary angles is equal to 180o
The Supplement of an angle x is 180 – x	The complement of an angle x is 90- x
Example  – 120o and 60o	Example 40o and 50o

Supplement of an angle

We now know that two angles are said to be supplementary if their sum is 180^o. So, if we are given one of the angles of the pair of supplementary angles can we find out the other angle?

The formula that is to define the relation be the pair of supplementary angles p and q is given by:

p + q = 180^o

Therefore, if we know one of the angles, using the above equation we can find out the value of the other angle.

Let us understand this by an example.

Suppose we are given the fact that there are two angles, namely ∠ P and ∠ Q which are said to supplement each other. We are also given the value of ∠ Q as 85^o. Now, what would be the value of ∠ P?

 We have the equation defining the relation between two supplement angles, p and q as

p + q = 180^o

Therefore,

∠ P + ∠ Q = 180^o

⇒ ∠ P + 85^o = 180^o

⇒ ∠ P  = 180^o – 85^o

⇒ ∠ P  = 95^o

Hence, the other angle if one of the supplement angles is 85^o will be 95^o

Solved Examples

Example 1    

Check whether the angles 125° and 53° are a pair of supplementary angles.

Solution              

We have learnt that the sum of two supplementary angles is always 180^o. Therefore, for the given two angles to be supplementary, their sum has to be equal to 180^o.

Hence, let us check the sum of the two given angles.

125° + 53° = 178^o

We can see that the sum of the two given angles does not equal to 180^o

Hence, the two given angles, 125° and 53° are not supplementary angles.

Example 2    

Find the value of ∠P  and  ∠Q if ∠P  and  ∠Q are supplementary angles and

∠P = 2x + 15 and   ∠Q = 5x – 38

Solution              

We have been given that ∠P  and  ∠Q are supplementary angles. We have also been given that ∠P = 2x + 15 and   ∠Q = 5x – 38

Now, we know that if two angles are supplementary their sum will be equal to 180^o. Now, since ∠P  and  ∠Q are supplementary angles, therefore.

∠ P + ∠ Q = 180^o ………………………………… (1)

But, in this case we have not been given a constant value of any of the two angles. However, we have been provided with a relational values of both and P and Q in terms of x which has been stated as   ∠P = 2x + 15 and   ∠Q = 5x – 38        

Therefore, in order to find the values of ∠P  and  ∠Q we will have to find the value of x. To get the value of x, first we should replace the values of ∠P  and  ∠Q  in the given equation  (1). Substituting these values we will get:

2x + 15 + 5x – 38 = 180

⇒ 7x – 23 = 180

⇒ 7x = 180 + 23

⇒ 7x = 203

⇒ x = 203/7 = 29

Therefore, x = 29^o

Now, that we have the value of x, we can obtain the value of ∠P  and  ∠Q 

∠P   = 2x + 15

⇒ ∠P   = ( 2 x 29 )+ 15

⇒ ∠P   = 58 + 15

⇒ ∠P   = 73^o

Also,

 ∠Q  = 5x – 38

 ∠Q  = ( 5 x 29 ) – 38

∠Q  = 145 – 38

∠Q  = 107^o

Therefore, the values of the two supplementary angles are ∠P   = 73^o and ∠Q  = 107^o

We can also check whether our answer is correct by substituting the values of ∠P  and  ∠Q in equation (1)

Substituting the values, we will get.

L.H.S

∠ P + ∠ Q

=73^o + 107^o

= 180^o = R.H.S Hence our answer is correct.

Example 3    

Calculate the value of θ in the figure below. Also, find the value of the three angles.

Solution              

From the given figure we can see that the given line is a straight line and three angles are formed on this straight line. Hence the sum of these three angles will be equal to 180^o. Therefore,

5q  + 4  + $\Theta$ – 2 + 3q + 7 = 180^o

⇒ 9$\Theta$ + 9 = 180^o

⇒ 9$\Theta$ = 180^o – 9

⇒ 9$\Theta$ = 171^o

⇒ $\Theta$ = 171/9^o

⇒ $\Theta$ = 19^o

Now that we know the value of $\Theta$ we can find the value of the three angles. Substituting the value of q in the three angles we will get,

First angle = 5 $\Theta$ + 4   = ( 5  x 19 ) + 4 = 95 + 4 = 99^o

Second angle =  $\Theta$ – 2 = 19 – 2 = 17^o

Third angle = 3$\Theta$ + 7 = ( 3 x 19 ) + 7 = 57 + 7 = 64^o

Hence, the three angles will be 99^o, 17^o, and  64^o

Example 4    

The ratio of a pair of supplementary angles is 1 : 8. Find the two measures of the two angles?

Solution              

We have been given that the ratio of a pair of supplementary angles is 1 : 8. Now, we also know that two angles are said to be supplementary if their sum is 180^o. This means that the sum of these two angles should also be equal to 180^o.

Let the two angles be represented by x and 8x.

This means that

x + 8x = 180^o

⇒ 9x = 180^o

⇒ x = 20^o

Now that we know the value of x we can find out the value of the other two angles as well.

We have,

First angle = x  = 20^o

Second angle = 8x = 8 x 20 = 160^o

Hence, the supplementary angles will be 20^o and 160^o

Example 5    

Find the supplement of the angle (20 + y)°.

Solution              

We have been given that out of a pair of supplementary angles, one of the angles is (20 + y)°. We need to find the supplement of this angle.

Now, we know that for two angles to be supplementary, their sum must be equal to 180^o. we have also learnt that if one of the angles of the pair of supplementary angles is p, the other angles would be 810 – p.

Therefore, if one of the angles is (20 + y)°, the other angle will be 180° – (20 + y)°

= 180° – 20° – y°

= (160 – y) °

Hence, if, for a pair of supplementary angles, one angle is (20 + y)° , the other angle will be (160 – y) °

Example 6    

If angles of measures (x — 2)° and (2x + 5)° are a pair of supplementary angles. Find the measure of the two angles.

Solution              

We have been given that the pair of angles that are a supplement to each other are – (x — 2)° and (2x + 5)°

Now, we know that two angles are said to be supplementary if their sum is 180^o. This means that the sum of these two angles should also be equal to 180^o. In other words, since (x – 2)° and (2x + 5)° represent a pair of supplementary angles, then their sum must be equal to 180°.

Therefore, we get the equation, (x – 2) + (2x + 5) = 180

We will solve this equation for x

x – 2 + 2x + 5 = 180

⇒ x + 2x – 2 + 5 = 180

⇒ 3x + 3 = 180

⇒ 3x = 180 — 3

⇒ 3x = 177

⇒ x = 177/3

⇒ x = 59°

Now, that we know the value of x we can find the value of the two angles.

First angle = x – 2 = 59 – 2 = 57°

Second angle = 2x + 5 = ( 2 × 59 ) + 5 = 118 + 5 = 123°

Therefore, the two supplementary angles are 57° and 123°. 

Summary & Key Facts

1. Two angles are said to be supplementary if their sum is 180^o.
2. When the sum of two angles is 180^o, i.e. when two angles are supplementary angles, they are said to be supplements of each other.
3. The angle formed by a straight line is always equal to 180^o
4. The formula that is to define the relation be the pair of supplementary angles p and q is given by – p + q = 180^o
5. A straight line is an infinite length line that does not have any curves on it. The angle formed by a straight line is always equal to 180^o
6. Two angles are said to be adjacent if they have a) a common vertex b) a common arm and c) the other two arms are on opposite sides of the common arm, i.e. they must not overlap each other.
7. If the sum of the adjacent angles is 180^o, they are said to be supplementary angles. Such angles are called a linear pairs of angles.
8. Non-adjacent supplementary angles are the angles that are a supplement to each other but are not adjacent, i.e. do not share a common vertex or an arm.
9. Complementary angles are the pair of angles that have the sum of 90^o.
10. Complementary angles are different from supplementary angles.

Recommended Worksheets

Angles (Architecture Themed) Worksheets
Understanding Supplementary, Complementary, Vertical and Adjacent Angles 7th Grade Math Worksheets
Triangles (Fashion Themed) Worksheets