Triangles And Their Types

Triangles

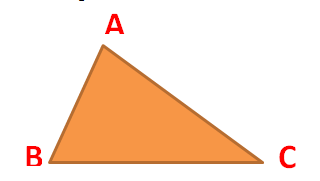
The word triangle is made from two words – “tri” which means three and “angle”. Hence, a triangle can be defined as a closed figure that has three vertices, three sides, and three angles. The following figure illustrates a triangle ABC:

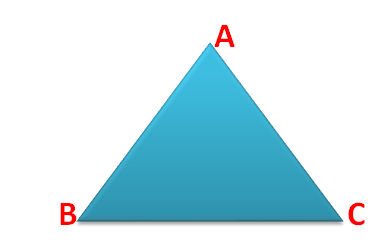
Vertices of a Triangle

In the above triangles, the three vertices are A, B and C.

Angles of a Triangle

The three angles are the angles made at these vertices, i.e. ∠A, ∠B and ∠C.  The angle formed at A can also be written as ∠BAC. Similarly, we can write ∠ABC and ∠ACB. These angles are also called the interior angles of a triangle. An exterior angle of a triangle is formed by any side of a triangle and the extension of its adjacent side.

Sides of a Triangle

The three sides of the triangle above are AB, BC and AC.

Properties of Triangles

Properties of triangles can be stated as under:

• Sides, Angles and Vertices

We already know that a triangle always has exactly three sides and three vertices. This is the basic property of any triangle.

• Angle Sum Property of a Triangle

The sum of the measure of the three interior angles of a triangle is always 180^o.

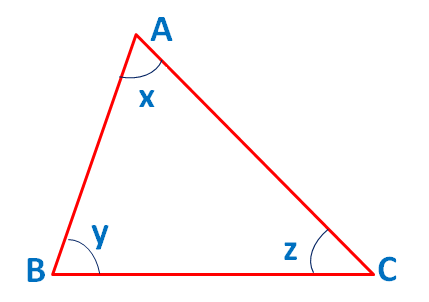
In the above triangle, ∠x + ∠y + ∠z = 180^o

• Triangle Inequality Property

According to the triangle inequality property, the sum of two sides of a triangle is always greater than or equal to the third side. If this sum is less than the third side, it is not possible to construct the triangle. For example, in a triangle ABC,

AB + BC ≥ AC

BC + AC ≥ AB

AB + AC ≥ BC

• Pythagoras Theorem

If one of the angles of a triangle is 90^o, the sides that make the right angle are called the base and the perpendicular while the third side is called the hypotenuse.

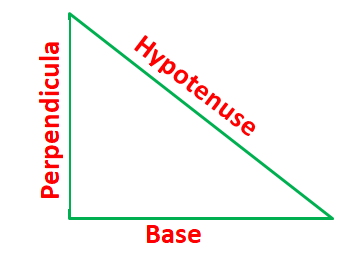
According to Pythagoras Theorem:

In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides.

Mathematically,

Base² + Perpendicular² = Hypotenuse²

Therefore, if “a” is the base, “b” is the perpendicular and “c” is the hypotenuse in a right angled triangle, then

c² = a² + b²

• Exterior Angle Property

According to this property, the exterior angle of a triangle is always equal to the sum of the interior opposite angles.

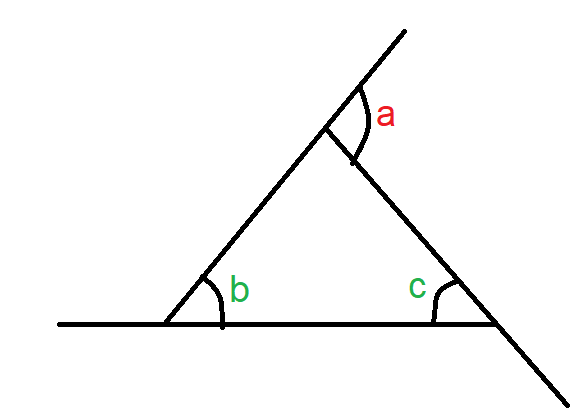
For example, in the above triangle, the exterior angle a equals the sum of the interior angles b and c.

∠a = ∠b + ∠c

Examples of Properties of Triangles

Example 1      

One of the angles of a triangle is 80^o and the other two angles are equal. Find these angles.

Solution

Since the other two angles are equal, let each of these angles be x. By angle sum property, the sum of the measure of the three interior angles of a triangle is always 180^o.

Therefore,

x +x + 80^o = 180^o

2x +80^o = 180^o

2x = 100^o

x = 50^o

The angles each measure 50^o

Example 2      

In a given ∆PQR, ∠P = 30^o, ∠Q = 50^o, find the measure of ∠R.

Solution

In ∆PQR

∠P + ∠Q + ∠R = 180^o

30^o + 50^o + ∠R = 180^o

∠R = 180^o – 80^o

∠R = 100^o

Example 3

The sum of the two angles of a triangle is equal to its third angle. What is the measure of the third angle?

Solution

The sum of all angles of a triangle is equal to 180^o

Let ∠P, ∠Q and ∠R be the three angles of the triangle such that

∠P + ∠Q = ∠R…………. (i)

We have,

∠P + ∠Q + ∠R = 180^o

∠R + ∠R = 180^o

2∠R = 180^o

∠R = 90^o

Hence, the measure of the third angle is 90^o.

Example 4

An exterior angle of a triangle is of measure 130^o and one of its interior opposite angles of major 60^o find the measure of the other interior opposite angle.

Solution

We know that,
exterior angle of a triangle = sum of the two opposite interior angles

Let the second interior angle be x

Then,
130^o = 60^o + x
x = 130^o – 60^o
x = 70^o
Hence, the other interior opposite angle is 70^o.

Example 5

The hypotenuse of a right angle triangle is 15 cm and the base of the triangle is 12 cm. Determine the perpendicular of the triangle.

Solution

Use the Pythagorean Theorem:

In a right angled triangle ABC

c²=a²+b² ……………………………….. (i)

where:

“c” is the hypotenuse, “b” is the base and “a” is the perpendicular.

We have been given that,

c = 15 cm

b = 12 cm

Substituting the values and b and c in the equation (i), we have,

(15)² = (12)² + a²

225 = 144 + + a²

a² = 225 – 144 = 81

Hence, a = 9

Therefore, the perpendicular of the triangle is 9 cm.

Example 6

The trunk of a tree cracks at a point 10 m above the ground. The tree falls and its top touches the ground at a distance of 24 m from the base of the tree find the actual height of the tree.

Solution

Suppose, that the actual height of the tree = h

Since, the trunk of a tree cracks at a point 10 m above the ground and its top touches the ground at a distance of 24 m from the base of the tree, it can be visualised as shown in the diagram below:

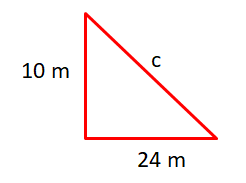
We can clearly see that in the above triangle,

Base = 24 m

Perpendicular = 10 m

Let the hypotenuse be “c”.

The height of the tree would be given by adding the perpendicular to the hypotenuse.

In order to find the hypotenuse, we need to apply the Pythagorean Theorem.

c² = (10)² + (24)²

c² =100 + 576

c² = = 676

c = 26 cm

Height of the tree = Perpendicular + Hypotenuse = 10 cm + 26 cm = 36 cm

Example 7

One of the exterior angles of a triangle is 80^o and the interior opposite angles are in the ratio 3 : 5. Find the angles of the triangle.

Solution

Let ∠ACX be the exterior angle of triangle ABC at C such that ∠ACX = 80^o. Clearly, ∠A and ∠B are the interior opposite angles as shown in the figure.

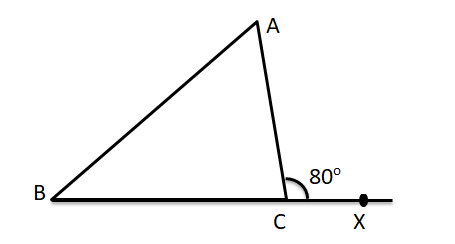
It is given that ∠A : ∠B = 3 : 5.

Therefore, let ∠A = 3x^o and ∠B = 5x^o

∠ACX = ∠A + ∠B

⇒ 80^o = 3x + 5x

⇒ 8x = 80^o

⇒ x = 10^o

∠A = 3x^o = 30^o and ∠B = 5x^o = 50^o

Now, ∠A + ∠B + ∠C = 180^o

⇒30^o + 50^o + ∠C = 180^o

⇒80^o + ∠C = 180^o

⇒∠C = 180^o – 80^o

⇒∠C = 100^o

Hence, the three angles of the triangle are ⇒∠C = 30^o, 50^o and 100^o

Example 8

A man steadily goes 10 m due east and then 24 m due north. Find the distance from the starting point.

Solution

Let the initial position of the man be O and his final position be B. Since the man goes 10 m due east and then 24 m due north, hence ∆OAB is a right angle.

By Pythagoras theorem, we have,

OB² = OA² + AB²

OB² = 10² + 24²

OB² = 100 + 576 = 676

OB = 26 m

Hence the man is at a distance of 26 m from the starting point.

The Seven Types of Triangles

Triangles can be classified based on the measure of their sides as well as their angles.

On the basis of the sides, triangles can be classified as Equilateral triangle, Isosceles triangle and scalene triangle.

Equilateral Triangle

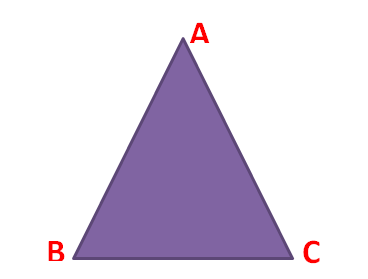
A triangle is said to be an equilateral triangle if all its sides are equal. Also, if all the three sides are equal in a triangle, the three angles are equal.

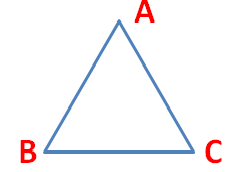
Therefore, in an equilateral triangle ABC, ∠A = ∠B = ∠C = 60^o

Isosceles Triangle

A triangle is said to be an Isosceles triangle if its two sides are equal. If two sides are equal, then the angles opposite to these sides are also equal.

For example, in the following triangle, AB = AC. Therefore ∆ABC is an Isosceles triangle.

Since AB = AC

 ∠B = ∠C

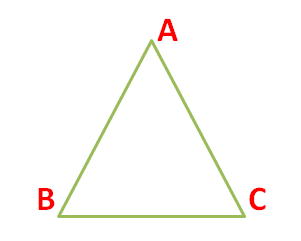
Based on the interior angles, the Isosceles triangle can further be divided into the following three types:

Right Isosceles Triangle

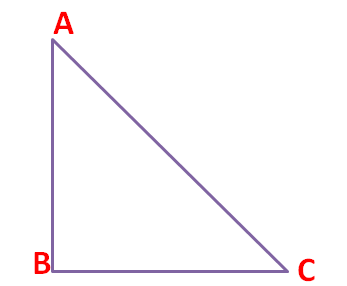
A triangle is said to be a right isosceles triangle if apart from two sides being equal, one of the angles of the triangle is a right angle, i.e. 90^o_. Suppose, we have a triangle, ABC where AB = BC and ∠ABC = 90^o.  Then such a triangle is called a right isosceles triangle which would be of a shape similar to the below figure.

Acute Isosceles Triangle

A triangle is said to be an acute isosceles triangle if apart from two sides being equal, all the three interior angles of the triangle are acute angles, i.e. all the three angles are less than 90^o. Suppose, we have a triangle, ABC where AB = BC and all the three angles are acute angles.  Then such a triangle is called an acute isosceles triangle which would be of a shape similar to the below figure.

Obtuse Isosceles Triangle

A triangle is said to be an obtuse isosceles triangle if apart from two sides being equal, one of the angles of the triangle is an obtuse angle, i.e. greater than 90^o_. Suppose, we have a triangle, ABC where AB = BC and ∠ABC > 90^o.  Then such a triangle is called an obtuse isosceles triangle which would be of a shape similar to the below figure.

Scalene Triangle

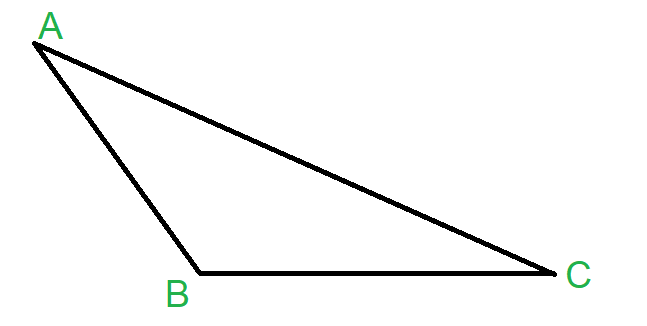
A triangle is said to be a scalene triangle if none of its sides are equal. In a scalene triangle, since none of the sides are equal, all the three interior angles are unequal as well.

Based on the interior angles, a scalene triangle can further be divided into the following three types:

Right Scalene Triangle

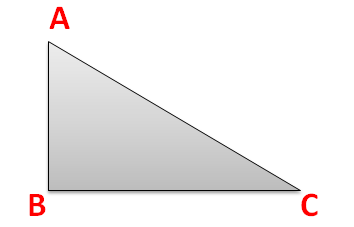
A triangle is said to be a right scalene triangle if apart from no side of it being equal, one of the angles of the triangle is a right angle, i.e. 90^o_. Suppose, we have a triangle, ABC where AB ≠ BC ≠ CA and ∠ABC = 90^o.  Then such a triangle is called a right scalene triangle which would be of a shape similar to the below figure.

Acute Scalene Triangle

A triangle is said to be an acute scalene triangle if apart from none of its sides being equal, all the three interior angles of the triangle are acute angles, i.e. all the three angles are less than 90^o. Suppose, we have a triangle, ABC where AB ≠ BC ≠ CA and all the three angles are acute angles.  Then such a triangle is called an acute scalene triangle which would be of a shape similar to the below figure.

Obtuse Scalene Triangle

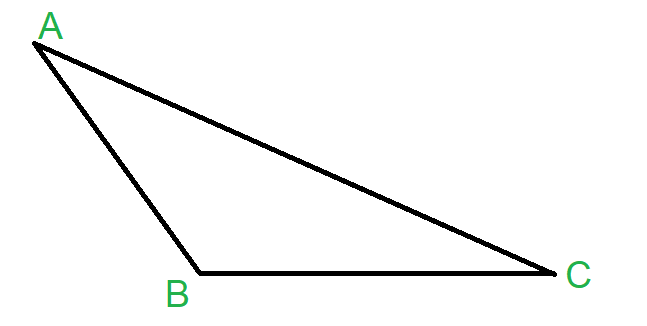
A triangle is said to be an obtuse scalene triangle if apart from none of its sides being equal, one of the angles of the triangle is an obtuse angle, i.e. greater than 90^o_. Suppose, we have a triangle ABC, where, AB ≠ BC ≠ CA and the angle formed at vertex A, ∠ABC > 90^o.  Then such a triangle is called an obtuse scalene triangle which would be of a shape similar to the below figure.

Remember

• A triangle cannot have more than one right angle.
• A triangle cannot have more than one obtuse angle.
• In a right angled triangle, the sum of the two acute angles is 90^o.
• The three sides and three angles of a triangle are together called the six parts of the elements of the triangle.
• A triangle is said to be
• an equilateral triangle if all its sides are equal
• an isosceles triangle if two of its sides are equal
• a scalene triangle if none of its sides are equal
• A triangle is said to be
• an acute triangle is each of its angles measures less than 90^o
• a right triangle if one of the angles measures 90^o
• an obtuse triangle if one of the angles measures more than 90^o
• The sum of all the angles of a triangle is 180^o

A quick check on what we have learned about Triangles

A. Choose the correct option (MCQs)

1. The measure of each angle of an equilateral triangle

a)     60^o                             b)     90^o                   c)      45^o                   d)     30^o

2.  A triangle which has sides of measure 5 cm 6.7 cm and 8.3 cm is of the type

 a)      Scalene                b)     Isosceles       c)      Equilateral    d)     Right angled               

3.  If the angles of a triangle are in the ratio 1 : 1 : 4, the triangle is

 a)      Right angled      b)     Acute angled        c)      Obtuse angled            d)    None of the above

4.  A triangle has angles

 a)      one acute           b)     two acute               c)      at least two acute     d)    at most two cute

B. Fill in the Blanks

1. In a right angle triangle side opposite to the right angle is called the __________________.

2. The sum of interior angles of a triangle is ___________________.

3. A ______________ triangle has one angle of 90°.

4. In an obtuse triangle, the remaining two angles are ______________.

5. Every triangle has at least _____________ acute angle.

C. Find the measure of the third angle of the triangle

1. ∠A = 70°, ∠B = 80°

2. ∠A = 95°, ∠B = 25°

3. ∠A = 105°, ∠B = 30°

4. ∠A = 90°, ∠B = 55°

D. The angles of a triangle are in the ratio 2 : 3 : 7. What is the measure of the largest angle?

E. State True or False

1. In a triangle sum of squares of two sides is equal to the square of the third side.

2. The difference between the lengths of any two sides of a triangle is smaller than the length of the third side.

3. It is not possible to have a triangle in which two of the angles are right angles.

Answers

A. Choose the correct option (MCQs)

1. a
2. a
3. c
4. c

B. Fill in the Blanks

1. Hypotenuse
2. 180^o
3. right angled
4. acute
5. one

C. Find the measure of the third angle of the triangle

1. 30^o
2. 60^o
3. 45^o
4. 35^o

D. 105^o

E. State True or False

1. False
2. False
3. True

Recommended Worksheets

Scalene Triangles (Summer Camp Themed) Math Worksheets
Equilateral Triangles (Outer Space Themed) Math Worksheets
Isosceles Triangles (Holiday Cruise Ship Themed) Math Worksheets