Introduction
Whenever we see a round object such as a ring, a basketball, or a melon, we associate this with the shape of a circle. What makes this shape special? How do we measure it if, unlike most shapes, the shape we have is round?
In this article, we learn the fundamental concepts starting with definitions of the shape, then we quantify the properties of the circle by defining both its perimeter and then its area. While doing so, we will also try some examples to guide us in learning.
What is a Circle?
A circle, by definition, is a perfectly round shape.
In geometric terms, a circle is formed by a collection of equidistant points from a fixed point called its center.
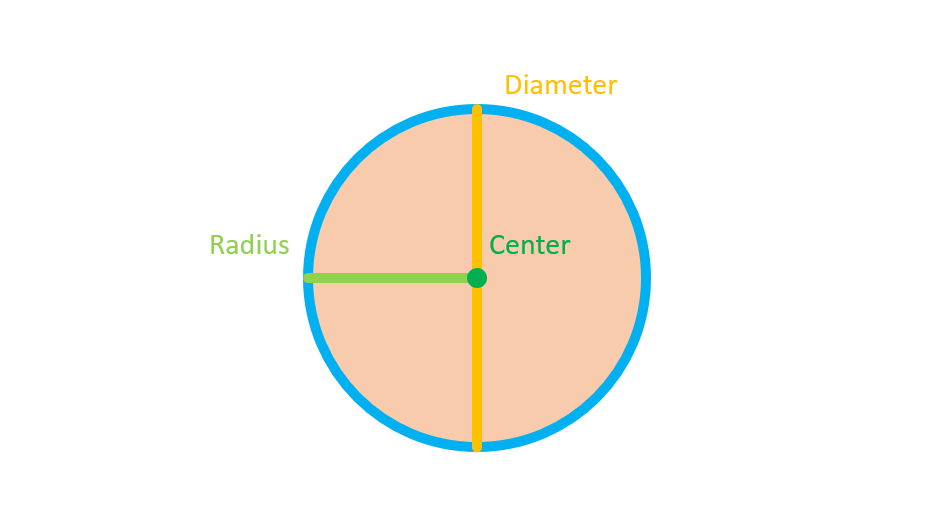
A line connecting the center to any point in the arc of a circle has a length equal to the radius of the circle. A diameter of a circle is any line passing through two points in the circle and its center.
What is a Perimeter?
We define the perimeter of a two-dimensional shape as a measure of the boundary enclosing it.
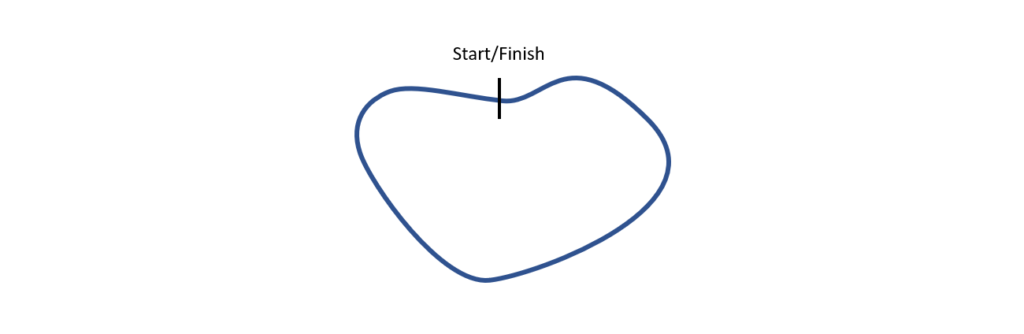
In an intuitive approach, we can relate the idea of a perimeter to how far we jog through a lap in the park. If we begin measuring the distance from the start of the lap, and then trace a closed path until we get back to the starting point, we can measure the perimeter of the park through the lap we have run across:
Thus, for any closed shape we can get its perimeter by taking the length of the edges enclosing the shape.
What is an Area?
On the other hand, we can define the area of a two-dimensional shape as a measure of the space it occupies in the two-dimensional plane.
Intuitively, we can think of shapes in a plane as objects in a room. Each object takes up some space in the room, depending on the kind of object and its size. In this sense, we can measure a shape’s area through the shape’s dimensions.
What is Pi?
Before we proceed with computing for the perimeter and area of a circle, we also introduce a special number that will prove relevant to our computations later.
The mathematical constant pi, denoted by , is a number that relates the diameter of a circle to its circumference. If we measure the perimeter of a circle and divide it with the measure of its diameter, we get the approximate value of pi:
π≈3.1415926…
It is important to note that this constant is a non-terminating irrational number. This means that the exact decimal value of pi is a never-ending stream of numbers! However, for most cases we only need to round off the value of to the nearest hundredths:
π≈3.14
Perimeter of a Circle
From the definitions provided earlier, we can now discuss in detail the formula for solving the perimeter of a circle. We first derive the basic formula involved, provide intuitive insights, and then show how we apply this formula with some examples.
Derivation of the Perimeter Formula of a Circle
We know that the perimeter can be defined as the sum of the lengths of all edges covering a shape. In most polygons, we take this as the sum of the lengths of its sides. However, what happens in the case of a circle with no sides? We conduct a simple experiment to show how the perimeter of a circle is measured:
Suppose we cut out a circle whose diameter is one foot, and mark one point on the edge of the cutout as shown:
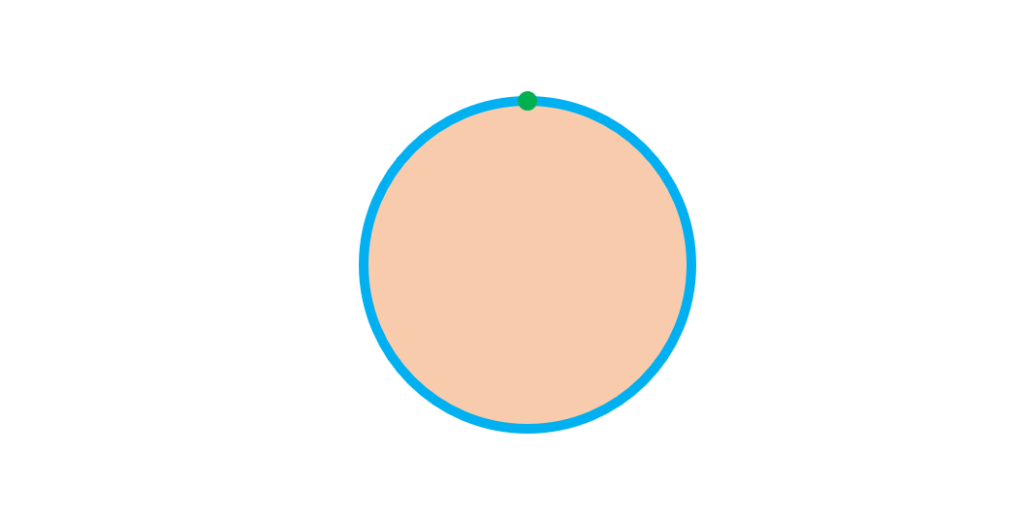
Next, we roll the circle across a straight line, starting from the mark until it completes one cycle:
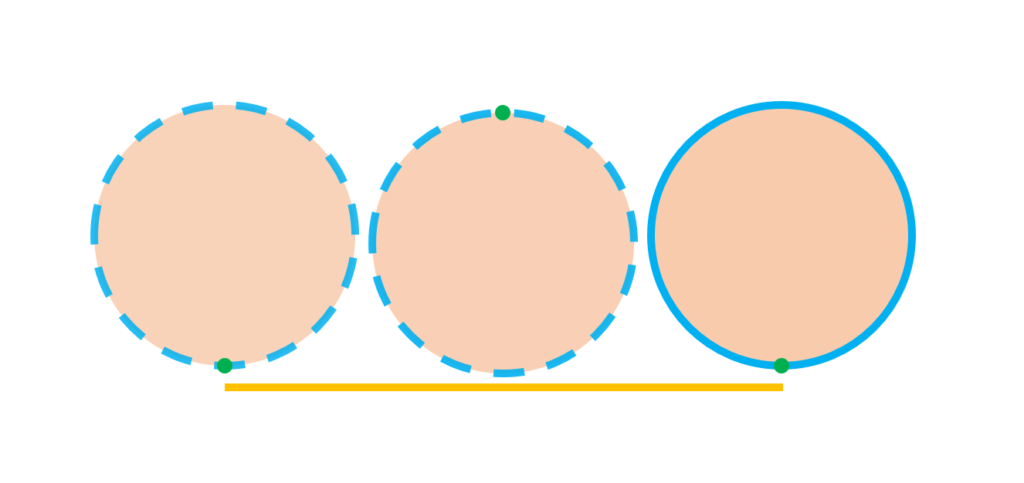
If we measure the length of the straight line, we are also measuring the perimeter of the cutout circle. And in this measurement, we get a number that is close to the constant !
Now, if we try larger circles—for a two-feet diameter we get twice the perimeter, for a three-feet diameter we get thrice the perimeter, and so on.
As such, we can generalize this observation about the perimeter of any circle whose diameter is given:
Perimeter=×Length of Diameter
Furthermore, we can describe the diameter of a circle as twice the length of its radius:
Length of Diameter=2×r
∴Length of Diameter=2r
Combining these expressions, we can then express the perimeter in terms of the radius r:
Perimeter=π×2r
What is the Perimeter Formula of a Circle?
From the previous derivation performed, the perimeter P of a circle with a known radius r is given by:
P=2πr
If the diameter d of the circle is given instead of a radius, we use an alternative formula that is expressed in terms of the diameter:
P=πd
We note that for both formulas, the unit of the perimeter is expressed in terms of the same units as with the radius/diameter given.
How is it Used?
As a practice on how to apply the formula, let us work together on finding the perimeter of the circle shown below:
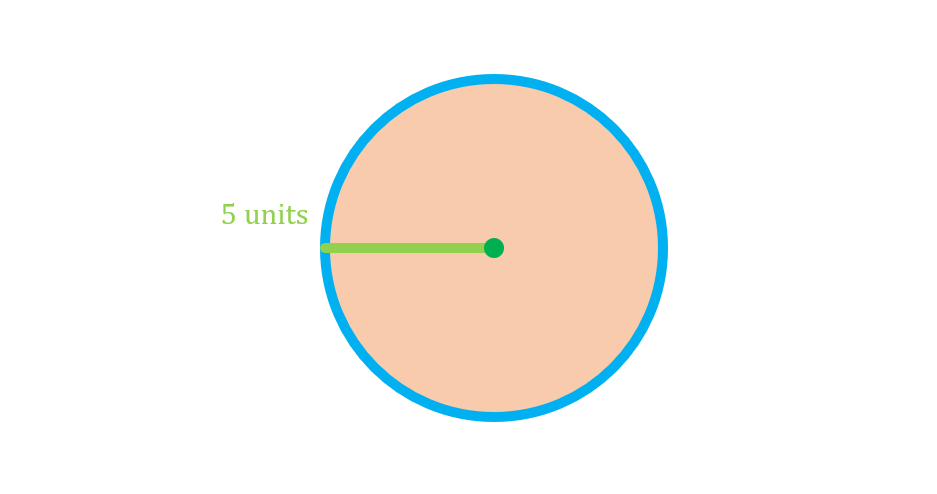
From the given figure, we are given the radius of the circle to be 5 units. Hence, we can say that:
r=5 units
Moreover, since the radius is known, we can use the Perimeter Formula in terms of the radius r:
P=2πr
We then substitute the given radius to the formula, along with an approximate value of π≈3.14 to get:
P=2×5 units×3.14
Then, multiplying the numbers together we obtain the perimeter of the circle:
P=31.4 units
We then conclude that the perimeter of the circle is 31.4 units. This quantity is expressed in terms of the same units as the radius.
Area of a Circle
Following the Perimeter Formula of a circle, we can also find its area through a given radius or diameter.
What is the Area Formula of a Circle?
The area A of a circle whose radius r is known can be expressed using the formula:
A=πr2
If the radius is not known but a diameter d is provided, we have an alternative formula that is expressed in terms of the diameter:
A=$\pi\:(\frac{d}{2})^2$
This holds since the length of a circle’s radius is half of the length of a circle’s diameter:
r=$\frac{d}{2}$
We note that for both formulas, the unit of the area is expressed in terms of squared units of the given radius/diameter.
How is it Used?
Again, we practice what we have learned so far by working on the same guided example as earlier, but for finding the area of the circle:
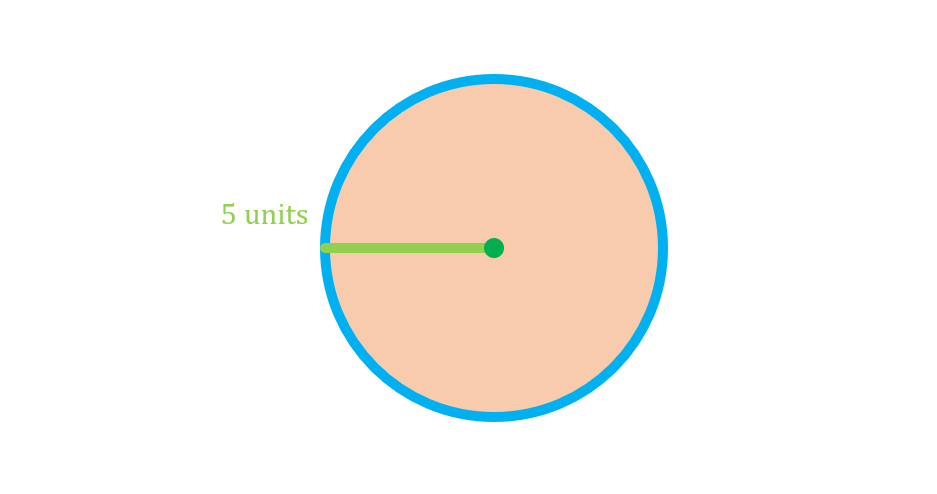
From the given figure, we are given the radius of the circle to be 5 units. Hence, we can say that:
r=5 units
Moreover, since the radius is known, we can use the Area Formula in terms of the radius r:
A=πr2
We then substitute the given radius to the formula, along with an approximate value of π≈3.14 to get:
A=3.14×(5 units)2
Afterward, we take the square of the radius to get:
A=3.14×25 units2
Then, multiplying the numbers together we obtain the area of the circle:
A=78.5 units2
We then conclude that the area of the circle is 78.5 units2. This quantity is expressed in terms of squared units of the radius.
Problem-Solving Examples
We can now proceed to solve sample problems to apply what we have learned so far. Each problem tackles different formulas discussed and gives us a challenge on how to solve through the information given to us.
Perimeter of a Circle
Sample Problem 1:
What is the perimeter of a circle whose radius is 10 centimeters?
Solution:
We recall that the perimeter P of a circle is given by the formula:
P=2πr
With the given radius r=10 cm and an approximate value of π≈3.14, we substitute these values into the formula:
P=2×3.14×10 cm
Finally, by multiplying the numbers together we obtain the value of the perimeter to be:
P=62.8 cm
Therefore, we conclude that the perimeter of the circle is 62.8 cm.
Sample Problem 2:
Suppose we have a donut whose outside diameter is 6 inches and has a hole with a diameter of 1.5 inches. Solve for the following:
- What is the outer perimeter of the donut?
- What is its inner perimeter?
- What is the total perimeter of the donut?
Solution:
- We observe that the outside diameter of the donut is given instead of its radius. Hence, we can use the other formula for the perimeter P of a circle:
Pout=πd
Using the above formula, we substitute the given diameter d=6 in. We also note that an approximate value of π=3.14 is used:
Pout=3.14×6 in
Lastly, we multiply the two numbers to get the value of the perimeter:
Pout=18.84 in
Therefore, the outer perimeter of the donut is 18.84 inches.
- Like Part A, we use the other formula for the perimeter P of a circle:
Pin=πd
Substituting the given diameter d=1.5 in and an approximate value of π=3.14, we get:
Pin=3.14×1.5 in
Lastly, we multiply the two numbers to get the value of the perimeter:
Pin=4.71 in
Therefore, the inner perimeter of the donut is 4.71 inches.
- We take the total perimeter PT of the donut by adding the outer and inner perimeters of the donut:
PT=Pout+Pin
Substituting the computed perimeter values from Part A and Part B, we have:
PT=18.84 in+4.71 in
Lastly, by adding the two numbers we can get the value of the total perimeter:
PT=23.55 in
Therefore, the total perimeter of the donut is 23.55 inches.
Sample Problem 3:
Alex wants to make a customized cup holder. To do that, she needs to wrap five rings made of wire around the body of the cylindrical cup. If the cup has a diameter of 5.5 centimeters, how much wire does she have to prepare for the cup holder?
Solution:
We note that the radius of the cup is given by r=5.5 cm. For a given radius, the perimeter P can be computed using the formula:
P=2πr
Hence, we can substitute the given values, with π≈3.14 into the above equation to get:
P=2×3.14×5.5 cm
We then simplify the equation by taking the product of the numbers together:
P=34.54 cm
Thus, Alex needs 34.54 cm per ring to wrap around her cup. To get the total length of wire required, we multiply the perimeter computed earlier by the number of rings she needs:
PT=34.54 cm×5 rings=172.7 cm
With the total perimeter PT computed to be 172.7 cm, then the amount of wire Alex needs for her customized cup holder is also 172.7 centimeters.
Area of a Circle
Sample Problem 4:
Suppose we use the same circle from Sample Problem 1 whose radius is given by 10 centimeters. What is the area of the circle?
Solution:
We recall that the area A of a circle is given by the formula:
A=πr2
With the given radius r=10 cm, and an approximate value of π≈3.14, we substitute these into the formula to get:
A=3.14×10 cm2
Getting the square of the radius, we have:
A=3.14×100 cm2
Finally, by multiplying the three numbers we can compute for the value of the area:
A=314 cm2
Hence, the area of the circle is 314 cm2.
Sample Problem 5:
Julie wants to order a round 16″ vegetable pizza for her neighbor Clark. When she arrived at the pizza parlor, she was offered two 10″ pizzas for the same price. Julie wants to get the most out of her money. Will she get more pizza by availing of two smaller pizzas instead?
Solution:
We first observe that the diameter of both pizzas is given to us. For a given diameter d, the area A of the circle can be expressed using the formula:
A=$\pi\:(\frac{d}{2})^2$
Then, we solve for the area of the larger pizza. Substituting the given diameter d=16 in, and using an approximate value of π≈3.14, we plug these values in the formula to get:
Alarge=3.14×($\frac{16 in}{2}$)2
Dividing the diameter by two, we simplify the fraction inside the parentheses. We note that we are effectively taking the radius of the circle using the given diameter:
Alarge=3.14×( 8 in )2
Then, we proceed by taking the square of the radius:
Alarge=3.14×64 in2
Thus, the area of the larger pizza can be obtained by multiplying the numbers:
Alarge=200.96 in2
Next, we proceed to solve for the combined area of the two smaller pizzas. Each 10″ pizza has an area equal to:
Asmall=3.14×$(\frac{10 in}{2})$2
Repeating the same steps as the larger pizza, we simplify the area of each smaller pizza to be:
Asmall=78.5 in2
Taking the combined area of two pizzas, we add their areas together:
Acombined=78.5 in2+78.5 in2
∴Acombined=157 in2
Finally, we compare the area of the larger pizza and the combined area of the smaller pizzas offered to Julie. Since the area of the larger pizza is 200.96 in2 and the combined area of the smaller pizzas is 157 in2, we can say that the combined area is smaller than the area of the larger pizza:
Acombined<Alarger
Therefore, we conclude that Julie will get less pizza by availing of two 10” pizzas instead of one 16” pizza.
Sample Problem 6:
Suppose the city management wants to build a fountain inside a park. The round base of the fountain is estimated to measure 9 meters in radius. If the cost of construction is set at $800 per square meter worked, what is the estimated total cost to build the fountain?
Solution:
We first note that the fountain’s round base has a radius r=9 m. We are asked to determine the budget required to work on the fountain, based on the total land area to be worked on. Hence, we first solve for the total area covered by the fountain’s base, then apply ratio and proportion to solve for the estimated budget required by city management.
To get the area of the round base, we use the formula for the area A of a circle given its radius r:
A=πr2
We then substitute the known radius, and use an approximate value of π≈3.14 into the formula:
A=3.14×( 9 m )2
Taking the square of the radius, we have:
A=3.14×81 m2
Hence, the area of the base can be obtained by multiplying together these numbers:
A=254.34 m2
To determine the estimated cost of construction, we apply the given estimated cost per square meter as shown below:
\$800=1 m2
For the computed area of the round base A=254.34 m2, the estimated budget C required is given by:
C=254.34 m2 ($\frac{\$800}{1 m^2}$)=\$203,472
Therefore, the city management requires an estimated budget of $203,472 for the construction of the park fountain.
Summary
A circle is a perfectly round shape. It is formed by a collection of equidistant points from a fixed center.
A line connecting the center to any point in the arc of a circle is a radius of the circle. A diameter of a circle is any line passing through two points in the circle and its center.
A perimeter is a measure of the boundary enclosing a shape. It can be obtained by taking the length of the edges enclosing the shape.
On the other hand, an area is a measure of the space a shape occupies in a 2D plane. This quantity is dependent on the dimensions of the shape.
The mathematical constant pi can be expressed as the ratio between the circumference of a circle and its diameter. It can be approximated as π≈3.14.
The perimeter P of a circle with a known radius r is given by the following formula:
P=2πr
Alternatively, its perimeter can also be expressed in terms of the diameter d:
P=πd
The area A of a circle whose radius r is known can be determined using the formula:
A=πr2
Alternatively, its area can also be expressed in terms of the diameter d:
A=$\pi\:(\frac{d}{2})^2$
Recommended Worksheets
Spatial Skill: Circles (New Year’s Eve Themed) Math Worksheets
Circumference of a Circle (Summer Party Themed) Worksheets
Area of a Circle (Home Decorations & Furniture Themed) Worksheets









