Introduction
In mathematics, a number is a value of a continuous quantity that can represent a distance along a line (or alternatively, a quantity that can be represented as an infinite decimal expansion). It was introduced in the 17th century by René Descartes, who distinguished between real and imaginary roots of polynomials.
The numbers include all the rational numbers, such as the integer −5 and the fraction 4/3, and all the irrational numbers, such as $\sqrt{2}$(1.41421356…, the square root of 2, (an irrational algebraic number). Included within the irrationals are the real transcendental numbers, such as π (3.14159265…). In addition to measuring distance, numbers can be used to measure quantities such as time, mass, energy, velocity, and many more. The collection of these numbers are called Real numbers and the set of real numbers is denoted using the symbol R and is sometimes called “the reals“.
History
A number line is an abstract notion which evolved early 20th century. A number line should be distinguished from the solid and geometrical line. A solid number line or an interval is an image that came into existence in the ancient world. As a notion, a geometrical line or axis formed by analysis in the period of time in 16th to 18th century, The notion of a right line or (Right-hand line or now known as positive line of real number) a curve as a locus emerged in 17th century in the earliest work on analysis by L’Hospital (1696).
As a concept, a number line formed in works of Cantor and Dedekind, however, the term itself, first known as a “Number Scale” and thereafter, as a “Number Line” has been used since 1912. The positive and negative numbers together form a complete-scale extending in both directions from zero”
Definition
Number Line:
A number line is a visual representation of real numbers on a straight line. That line is used to compare every real numbers (R) that are placed at equal intervals on an infinite line that extends horizontally on both sides to infinity (theoretically) Every point of the number line is assumed to correspond to a real number, and every real number to a point. The number line contains all real numbers such a Rational Numbers (Fractions and Integers) and Irrational Number (Algebraic Numbers like $\sqrt{2}, \, \sqrt{3}\,,\frac{1}{\sqrt{2}}$ and Transcendental Numbers like , ).
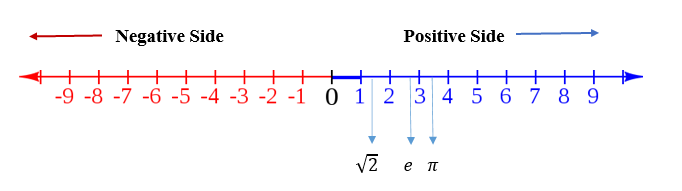
Numbers on the Number Line
Arithmetic operations of numbers can be better explained on a number line. To begin with, one must know to locate numbers on a number line. Zero is the middle point of a number line. All (natural numbers) positive numbers occupy the right side of the zero whereas negative numbers occupy the left side of zero on the number line. As we move on to the left side value of a number decreases. For example, 1 is greater than -2. In a number line, integers, fractions, and decimals can also be represented easily
Representation of Number Line
Below are the steps the numbers to represent on number line:
- Draw a straight line.
- Mark a point in the middle of the line as 0.
- Mark another points to the right of 0. Label them as 1, 2, 3… The distance between these marks must be uniform. They are said to be at a unit distance from one another.
- Mark another points to the left of 0. Label them as -1, -2, -3… The distance between these marks must be uniform. They are said to be at a unit distance from one another.

Properties of Number Line
1. Every Real number on the number line is well situated and well define on the line. Every number is defined on equal distance or segment along its length.
2. Every number on the line treated as a point on the number line.
3. There are infinitely many rational and irrational numbers in any two rational or irrational number on the real number line (Archimedean Property).
4. Every real number on this line is well ordered i.e. for any two numbers x and y from the number line there exist a relation between them i.e. either x>y, x<y or x=y.
Example 1: Chose two numbers from the line say 5 and 8 so we saw there is a relation between them here 5<8
5. Addition and Multiplications are Commutative on number line
6. Numbers are closure under Addition, Subtraction and Multiplication on Real line.
(Closure: – Let * be an any binary operation on a set, then * is said to be closure on that set if for any two elements from the set x and y (say) Then x*y also the element of that set)
7. If we collect all points from the number line in a set, then we get the set of real numbers and the image looks like

Where,
R= Set of all Real Numbers
Q= Set of all Rational Numbers
Z= Set of all Integers
N= Set of all Natural Numbers



Addition on Number Lines
When we add two positive numbers, the result will always be a positive number. Hence, on adding positive numbers direction of movement will always be to the right side.
Example: addition of 1 and 5 (1 + 5 = 6)
Here the first number is 1 and the second number is 5; both are positive. First, locate 1 on the number line. Then move 5 places to the right will give 6.

2. Adding Negative Numbers
When we add two negative numbers, the result will always be a negative number. Hence, adding negative numbers direction of movement will always be to the left side.
Example: the addition of -2 and -3 [(-2) + (-3) = -5]
Here, the first number is -2 and the second number is -3; both are negative. Locate -2 on the number line. Then move 3 places to the left will give -5.

Subtraction on Number
1. Subtracting Positive Numbers
When we subtract two positive numbers, move to the left as far as the value of the second number.
Example: subtract 5 from 2 ( 5 – 2 = 3 )
Here the first number is 2 and the second number is 5; both are positive. First, locate 2 on the number line. Then move 5 places to the left will give -3.

2. Subtracting Negative Numbers
When we subtract two negative numbers, move to the right as far as the value of the second number.
Example: Subtract -4 from -2 [ (-4) – (-2) = 2]
First, locate -2 on the number line. Then move 4 places to the right will give 2.

Multiplication on Number Line:
Multiplication is also known as repeated addition. To perform multiplication using a number line we move towards the right side of the number line for a given number of times.
Example: Multiply 𝟓 × 𝟑 using number line
Solution: Since this is multiplication, we will move towards the right side of the number line. Starting from zero, five groups of 3 equal intervals need to be formed on the number line. This way we will reach 15 forming 5 individual groups. Observe the following number line that shows 5 × 3 = 15.

Division to Represent on Number Line
Division on it is like the iterated or the repeated subtraction.
Example: 12 ÷ 2
If we have to divide 12 by 2, we start at 12. With an interval of 2 points, we move backwards one at a time till we reach 0. The number of jumps made is the solution. Here, it is 6. So, 12 ÷ 2 = 6.

Inequalities on number line:
The number line can be used to represent inequalities. Inequalities are shown as a line extending in one direction from a point. Graphing an inequality on a number line, is very similar to graphing a number. There are four cases of inequalities
- x > a ( x is greater than a )
- x < a ( x is less than a )
- x ≥ a ( x is greater than equal to a )
- x ≤ a ( x is less than equal to a )
For Example,
We consider x = 4 on number line.
We just put a little dot where the ‘4’

Now we consider the inequalities using the greater than, then less than, and then greater than equal and less than equal, all the cases that we have to do to make a graph of inequality on the number line.
Case 1: x > a ( x is greater than a )
A. Example: Consider the inequality x > 8
Solution: The inequality uses a greater than sign, and all that we have to do to graph the inequality is find the number, ‘9’ in this case and color in everything above or it.

B. Example: Consider another inequality x > -5
Solution: Here the number is -5. First we have to find the number in the number line then color it after the point ‘-5’ and tends to the right side of the direction.

Case 2: x < a ( x is less than a )
A. Example: Consider the inequality x < 5
Solution: The inequality uses a less than sign, and all that we have to do to graph the inequality is find the number, ‘5’ in this case and color in everything below or it.

B. Example: Consider another inequality x < -3
Solution: Here the number is -3. First we have to locate the number in the number line then color it after the point ‘-3’ and tends to the left side of the direction.

Case 2: x ≥ a ( x is greater than equal to a )
A. Example: Consider the inequality x ≥ 7
Solution: The inequality uses a greater than equal sign, and all that we have to do to graph the inequality is find the number, ‘7’ in this case and color in everything above or it.

B. Example: Consider another inequality x ≥ -10
Solution: Here the number is -10. First we have to locate the number in the number line then color it after the point ‘-10’ and tends to the right side of the direction.

Case 4: x ≤ a ( x is less than equal to a )
A. Example: Consider another inequality x ≤ -1
Solution: Here the number is -1. First we have to locate the number in the number line then color it after the point ‘-1’ and tends to the left side of the direction.

Important Note (Remark):
1. If the symbol is (≥ or ≤) then you fill in the dot, like example given below.

2. If the symbol is (> or <) then you do not fill in the dot like the bottom like example in the graph below

Addition of Numbers Without Using Number Line
When the numbers are large (> 10), then the use of number line is not convenient for their addition. Also, it is very time consuming to draw a number line every time, and perform the operation of addition.
There are four rules of addition on different numbers.
Rule No 1. ( Addition of two positive numbers)
To add a positive (+ ve) number to a positive (+ ve) number, the numbers should be added and positive sign should be attached to the sum obtained.
Example 1:
( +8 ) + ( +9 ) = +17 or 17
( +21 ) + ( +35 ) = +47 or 47
Rule No 2. (Addition of a positive to a negative number)
To add a positive number to a negative number, the numbers with smaller value should be subtracted from the number with bigger value and the sign of the bigger number should be attached to the answer
Example 2:
( +21 ) + ( -35 ) = -14
( +17 ) + ( -12 ) = +5 or 5
Rule No 3. (Addition of a negative to a positive number)
Adding a negative number to a positive number, the numbers with smaller value should be subtracted from the number with bigger value and the sign of the bigger number should be attached to the answer.
Example 3:
( -19 ) + ( +35 ) = +16 or 16
( -27 ) + ( +14 ) = -13
Rule No 4. (Addition of a negative to a negative number)
Adding a negative number to a negative number, the numbers should be added and negative sign should be attached to the sum obtained.
Example 4:
( -15 ) + ( -5 ) = -20
( -29 ) + ( -3 ) = -32
Column Addition
When adding lots of numbers together it is helpful to write them in columns, denoting units, tens and hundreds
Example: 9, 18, 27, 99, 114
| Hundreds | Tens | Units | |
| 9 | |||
| 1 | 8 | ||
| 2 | 7 | ||
| 9 | 9 | ||
| + | 1 | 1 | 4 |
| Ans: | 2 | 6 | 7 |
Facts Related with Addition:
- Addition is the operator used to describe adding two or more numbers together.
- The plus sign ‘+‘is used to denote an addition: 1 + 3.
- The + can be used multiple times as required: 1 + 2 + 3.
- For longer lists of numbers it is usually easier to write the numbers in a column and perform the calculation at the bottom.
- The word ‘sum’ or the symbol ∑ may also be used for addition.
- It doesn’t matter in which order you add a group of numbers.
- (Addition operator is commutative) together as the answer will always be the same: 1 + 2 + 3 + 4 gives the same answer (10) as 4 + 2 + 1 + 3.
- Adding 0 to any number makes no difference X + 0 = X.( 0 is the identity element in R (Real Number) with respect to + operator ).
Sign Rule: Relation between plus and minus sign under multiplication
| 1st term | 2nd term | Answer |
| + | + | + |
| + | – | – |
| – | – | + |
Some Questions regarding on Number Line:
Q 1. What is the number line example?
Answer: In mathematics, we define a number line as a straight line that has numbers located at equal intervals or segments all along its length. We can indefinitely extend a number line in any direction and is we generally represent it horizontally.
Q 2. Who is the smallest whole number?
Answer: The smallest whole number is zero.
Q 3. How many numbers can be represented in a number line?
Answer: A number line extends infinitely on both sides. Hence, we can represent infinitely many numbers on a number line and we represent all real numbers on the number line where we know the real numbers are uncountable.
Q 4. Who invented Number Line?
Answer: The English mathematician, John Wallis (1616 – 1703) is credited as the inventor of Number Line. For giving the meanings of negative numbers he invented the number line.
Q 5. How many even prime numbers are in there on the number line?
Answer: There is only one even prime number on the number line and it is 2.
Q 6. Can we divide any number by zero?
Answer: Dividing any number by zero does not make sense, because in Mathematics dividing by zero can be interpreted as multiplying by zero. There’s no number that we can multiply by zero to get a non-zero number. There’s no solution, so any non-zero number divided by 0 is undefined.
Q 7. Is 0 can divided by 7?
Answer: Yes can, zero can divided by 7
0 ÷ 7 = 0.
Practical Example: – If you have 0 pencil in your bag and you have 7 friends so everyone will get 0 pencil.
Q 8. What is the value of 0 ÷ 0?
Answer: The expression is undefined.
Because, the situation with is strange, because every number x in Real line satisfies . Because there is no single choice of x for which is defined so we treated as undefined.
Q 9. Is zero is an even number?
Answer: Yes, zero is an even number.
Q 10. If positive integers are placed on the left side of number line, then what does it indicate?
Answer: If positive integers are placed on the left side of number line, then those numbers are smaller than the numbers on the right side. For example, 10 is placed on the left side of 11, as 10 is less than 11.
Recommended Worksheets
Number Lines (Food Festival themed) Worksheets
Decimals in a Number Line (Birthday Themed) Worksheets
Fractions in the Number Line (Summer Themed) Worksheets









