Polynomials | Properties, Operations, Examples & Types

What will I learn from this article?

After reading this article, you will be able to:

properly define a polynomial;
determine the different composition of polynomials;
know the standard form of polynomials;
classify a polynomials based on the degree;
name a polynomial based on the number of terms;
apply the knowledge in solving polynomials;
use certain properties in performing different operation in polynomials; and
know the importance of learning polynomials

What is a polynomial?

Polynomials are algebraic expressions in which it is composed of variables and coefficients that involves the use of the basic mathematical operations; addition, subtraction, multiplication, and the positive integer exponentiation in variables.

Say, for example, 2x + 3 is a polynomial, as well as 3x² + 8x + 1.

In any single indeterminate x, a polynomial can always be written in the form:

anxn+an-1xn-1+…+a2x2+ax+a0

where, a_o, …, a_nare constants and x is the indeterminate.

The term “indeterminate” refers to the fact that x does not specify a specific value, though any value may be substituted for it.

What made up a polynomial?

The figure below shows one sample of a polynomial with its parts.

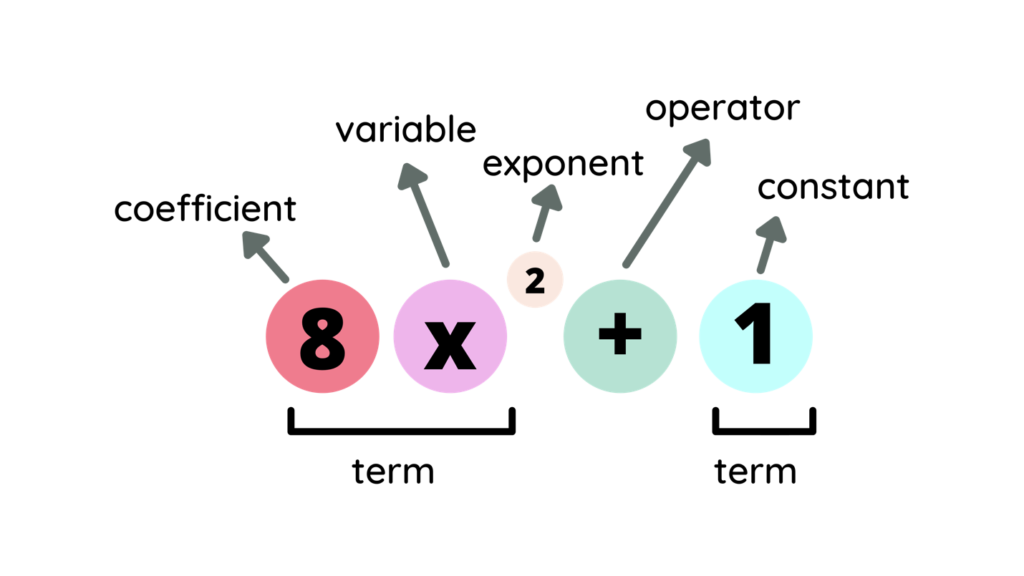
A coefficient refers to a number that is being multiplied by the variable.
A variable is a symbol or letter that works as a placeholder for a quantity that may assume any given value.
An exponent indicates the number of times a number is multiplied by itself.
An operator is a symbol that indicates an operation to be performed, such as addition, subtraction, multiplication, etc.
A constant term is a value or quantity that does not change. It is the fixed value in a mathematical statement.
A term can be a constant number, a variable, or a combination of constant and variable/s.

What is the standard form of a polynomial?

The standard form of a polynomial refers to the writing of a polynomial in which the exponent of variables is arranged in descending order. The table below examples of polynomials in a standard and non-standard form.

NON-STANDARD FORM	STANDARD FORM
3 + x	x + 3
4x – x² + 1	-x² + 4x + 1
5 + x³ + 6x⁵	6x⁵ + x³ + 5

What are the degrees of polynomial?

A polynomial degree is defined as the highest degree of any monomial contained within the polynomial. Thus, a polynomial equation with a single variable having the highest exponent value is referred to as a degree polynomial.

Some polynomials defined by their degree are called as a constant polynomial, linear polynomial, quadratic polynomial, cubic polynomial, and quartic polynomial.

Constant Polynomial

A constant polynomial is a polynomial with a degree of 0. This polynomial is also called as a zero polynomial.

Linear Polynomial

A linear polynomial is a polynomial in a degree 1. Say, for example, 2x and x + 3 are both examples of a linear polynomial.

Quadratic Polynomial

A quadratic polynomial is a polynomial in degree 2.

Cubic Polynomial

A cubic polynomial is a polynomial in degree 3.

Quartic Polynomial

A cubic polynomial is a polynomial with a variable having the highest exponent of 4.

To summarize the different degrees of polynomial, observe the table below.

POLYNOMIAL	DEGREE	EXAMPLE
Constant or Zero Polynomial	0	8
Linear Polynomial	1	5x + 2
Quadratic Polynomial	2	6x² + x + 9
Cubic Polynomial	3	10x³ + 2x² + 5x + 1
Quartic Polynomial	4	7x⁴ + 3x³ + 9x² + 10x + 1

What are the classifications of polynomials?

The terms of polynomials are the parts of polynomials that are separated by “+” and “–“. Thus, every part of a polynomial that contains either a variable or a constant is considered as a term.

Polynomials are classified into three types based on their number of terms. They are classified into three types of polynomials namely; monomial, binomial, and trinomial.

Monomial

A monomial is a polynomial or an algebraic expression that contains exactly one term. For a polynomial to be referred to as a monomial, the single term should be a non-zero term. Some examples of monomials are:

x
8x
3
6x³
-10x

Binomial

A binomial is a polynomial with exactly two terms. It is a binomial when either a sum or difference of two monomials. A few examples of binomial are:

2x + 3
4x² + 4
7x⁴ + 3y²
-x⁷+ 9xy³

Trinomial

A trinomial is an expression which is composed of exactly three terms. Some examples of trinomial are:

x³ + 2x + 1
8x⁶ + 3x² + 2
-4x⁵ + x³ + 9

To summarize the different classifications of polynomials, observe the table below.

CLASSIFICATION OF POLYNOMIAL	NUMBER OF TERMS	EXAMPLE
Monomial	1	8x
Binomial	2	4x + 3
Trinomial	3	7x² + 2x + 19

What are the properties of polynomials?

The following are some significant properties of polynomials, as well as some significant polynomial theorems.

Property 1: Division Algorithm

The division algorithm states that of a polynomial if the quotient of P(x) and g(x) is Q(x) with a remainder of R(x), then

Px=Gx∙Qx+R(x)

Property 2: Bezout’s Theorem

A polynomial P(x) is divisible by a binomial (x – a) if and only if P(a) = 0.

Property 3: Remainder Theorem

If P(x) is divided by (x – a) with a remainder r, then P(a) = r.

Property 4: Factor Theorem

A polynomial P(x) divided by Q(x) will result in R(x) with zero remainders if and only if Q(x) is a factor of P(x).

Property 5: Intermediate Value Theorem

If P(x) is a polynomial, and P(x) P(y) for (x < y), then P(x) takes every value from P(x) to P(y) in the closed interval [x,y].

Property 6:

The operations of addition, subtraction, and multiplication of polynomials P and Q result in a polynomial where,

Degree (P±Q)≤Degree (P or Q) Degree(P∙Q)=Degree (P) +Degree (Q)

Property 7:

If a polynomial P is divisible by a polynomial Q, then every zero of Q is also a zero of P.

Property 8:

If a polynomial P is divisible by two coprime polynomials Q and R, then it is divisible by (Q∙R).

Property 9:

If P(x)=a_nxⁿ+a_n-1x^n-1+…+a₂x²+ax+a₀ is a polynomial such that deg(P) = n$\geq$ 0 then, P has at most n distinct roots.

Property 10: Descartes’ Rule of Sign

The number of positive real zeroes in a polynomial function P(x) is equal to or less than the number of coefficient sign changes. Thus, if the K sign changes, the number of roots is either k or (k – a), where a is an even number.

Property 11: Fundamental Theorem of Algebra

At least one complex root exists for every non-constant single-variable polynomial with complex coefficients.

Property 12:

If P(x) is a polynomial with real coefficients and has one complex zero (x = a – bi), then x = a + bi will also be a zero of P(x). Also, x² – 2ax + a² + b² will be a factor of P(x).

What are the operations in polynomials?

There are four primary polynomial operations namely, addition of polynomials, subtraction of polynomials, multiplication of polynomials, and division of polynomials.

Addition of Polynomials

When adding polynomials, always add like terms, that is, terms with the same variable and power. Polynomials are always added to produce polynomials of the same degree.

To add polynomials:

Always see to it that the polynomials are in standard form.
Arrange in columns of like terms.
Add the columns.

Example #1

Find the sum of x + 3 and 2x + 4

Solution

To find the sum of x + 3 and 2x + 4, first, combine like terms. Thus,

x + 3
+ 2x + 4
———-
3x + 7
———-

Therefore, the sum of the two polynomials is 3x + 7.

Example #2

Solve for the sum of 2x² + 4x + 3 and x + 8.

Solution

Since the polynomials are already in their standard form, thus, by combining the like terms of 2x² + 4x + 3 and x + 8, the sum will be:

2x² + 4x + 3
+ x + 8
2x² + 5x + 11
—————–
3x + 7
—————–

Therefore, the sum of the two polynomials is 2x² + 5x + 11. Always remember that you can only add terms with the same variables and same exponents.

Example #3

Determine the sum of 5x⁵ + 4x + 3x² + 3 and 7x³ + 2x⁴ + x.

Solution

Step 1: Since the given polynomials are not in their standard form, arrange them in descending order. Thus, we will have 5x⁵ + 3x² + 4x + 3 and 2x⁴ + 7x³ + x.

Step 2: Arrange the polynomials in column and add. Thus,

5x⁵ + 3x² + 4x + 3
+ 2x⁴ + 7x³ + x
————————————-
5x⁵ + 2x⁴ + 7x³ + 3x² + 5x + 3
————————————-

Therefore, the sum of the two polynomials is 5x⁵ + 2x⁴ + 7x³ + 3x² + 5x + 3.

Example #4

What is the sum of xy and yx?

Solution

Observe that the two monomials have the same variable and of the same degree, thus, we can say that they are like terms.

Step 1: Arrange them in the same manner form. Thus, we will have xy and yx will be xy.
Step 2: Add the two monomials. Thus, xy + xy = 2xy.

Therefore, the sum of xy and yx is 2xy.

Subtraction of Polynomials

Subtracting polynomials is similar to addition, except for the operation type.

To subtract polynomials:

Arrange the polynomials in descending degrees.
Arrange in columns of like terms.
Change the signs of each term in the minuend.
Combine all the terms on each column.

Example #1

Find the difference of 3x + 8 and x + 4.

Solution

Step 1: Since the given polynomials are already in standard form thus, changing the sign of the minuend will be,

3x + 8

x + 4 -> – x – 4

Step 2: Solve the difference of the two polynomials.

         3x + 8
    – x – 4
—————–
      2x + 4
—————–

Therefore, the difference between the two polynomial is 2x + 4.

Example #2

Solve for the difference of 5x² + 2x – 3 and x² + 4x + 4.

Solution

Step 1: Change the sign of the minuend. Thus,

5x² + 2x – 3
– x² + 4x + 4 -> -x² – 4x – 4

Step 2: Find the difference of the polynomials.

5x² + 2x – 3
–x² – 4x – 4
—————–
4x² – 2x – 7
—————–

Therefore, the difference of the two polynomials is 4x² – 2x – 7.

Example #3

Subtract x⁴ + x³ – 8x² + 9x – 13 from 3x³ – x + 4.

Solution

In example #3, we are asked to subtract x⁴ + x³ – 8x² + 9x – 13 from 3x³ – x + 4, which means the minuend is x⁴ + x³ – 8x² + 9x – 13 and the subtrahend is 3x³ – x + 4. Thus,

3x³ – x + 4 – (x⁴ + x³ – 8x² + 9x – 13).

Step 1: Change the signs of the minuends. Thus,

3x³ – x + 4

– (x⁴ + x³ – 8x² + 9x – 13) -> -x⁴– x³+ 8x² – 9x + 13

Step 2: Arrange the two polynomials in column. Thus,

3x³ -x +4– x4-x3+8×2-9x+13

– x⁴ + 2x³ + 8x² – 10x + 17

Therefore, the difference of two polynomials is – x⁴ + 2x³ + 8x² – 10x + 17.

Take note that when subtracting two different polynomials, the sign of the highest coefficient will be the sign of the result when subtracted.

Multiplication of Polynomials

To multiply polynomials, you must:

Distribute each term of the polynomial to all the terms of the other polynomials.
Always remember that when multiplying polynomials, the laws of exponent are applied. Thus, multiplying the exponents of variables is simply adding the exponent.

Example #1

What is the product of x² and 4x + 3?

Solution

To get the product of the two polynomials, distribute x² to 4x + 3. Thus,

(x²)(4x + 3)
4x³ + 3x²

Therefore, the product of two polynomials is 4x³ + 3x².

Example #2

Determine the product of 2x + 7 and x + 4.

Solution:

Step 1: When multiplying binomial by another binomial, we use the method called FOIL method. The FOIL Method simply means First Term, Outer Term, Inner Term, and Last Term. Thus,

(2x + 7)(x + 4)

First Term: (2x)(x)² = 2x²

Outer Term: (2x)(4) = 8x

Inner Term: (7)(x) = 7x

Last Term: (7)(4) = 28

Step 2: Add all the terms. Thus,

2x² + 8x + 7x + 28
2x² + 15x +28

Therefore, the product of the two binomials is 2x² + 15x + 28.

Example #3

Find the product of 4x³ + 1 and 2x² + 3x + 9.

Solution

Distribute the first term of the first polynomial to each of the terms of the other polynomial. Thus,

(4x³ + 1)(2x² + 3x – 9)
= (4x³)(2x²) + (4x³)(3x) – (4x³)(9) + (1)(2x²) + (1)(3x) – (1)(9)
= 8x⁵ + 12x⁴ – 36x³ + 2x² + 3x – 9

Therefore, the product of a binomial and trinomial is 8x⁵ + 12x⁴ – 36x³ + 2x² + 3x – 9.

Division of Polynomials

Dividing two polynomials may result in a polynomial or a constant term. Quotients of two polynomials can also have a remainder.

To divide two polynomials, you may use the steps below:

Arrange the two polynomials in a standard form.
Use the long division method.
Check the first term and divide the terms accordingly.
Remember that the law of exponents applies when dividing two polynomials. Thus, dividing the exponents of the variables is simply subtracting the exponents.

Example

What is the quotient when x² + 5x + 6 is divided by x + 3?

Solution

Step 1:

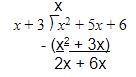Divide the first term of x + 3 to the first term of x² + 5x + 6. Thus, having x. Then, multiply x to x + 3 and subtract the product from x² + 5x + 6.

Divide x + 3 from 2x + 6. Since if we divide x from 2x, we will have 2. Then, multiply 2 to x + 3.

Therefore, the quotient is x + 2.

What is the significance of polynomials?

Polynomials are found in a wide variety of areas of mathematics and science. For instance, they are used to:

construct polynomial equations, which encode a wide variety of problems ranging from elementary word problems to complex scientific problems;
define polynomial functions, which appear in a variety of contexts ranging from elementary chemistry and physics to economics and social science; and
approximate other functions in calculus and numerical analysis.

Polynomials are used in advanced mathematics to construct polynomial rings and algebraic varieties, both of which are fundamental concepts in algebra and algebraic geometry.

Recommended Worksheets

Polynomials Worksheets
Multiplication of Polynomials (Universe Themed) Worksheets
Division of Polynomials (Labor Day Themed) Worksheets

Browse All Worksheets

We spend a lot of time researching and compiling the information on this site. If you find this useful in your research, please use the tool below to properly link to or reference Helping with Math as the source. We appreciate your support!