Introduction
Imagine you go to a store with a wallet that contains only paper money. What can be the smallest number of bills in your wallet? Of course, 0 – when there is no money in the wallet at all. Well, you wouldn’t go to the store without money at all. So, if you have money in your wallet, what is the smallest number of banknotes in your wallet? Yes, one paper bill. If you continue counting money, what will you have? One paper bill, two paper bills, three paper bills and so on. Here’s an illustration where in everyday life you can see whole numbers. And what you can do with these numbers – you will read in this article.
Definition of whole numbers
The numbers 1, 2, 3, 4 … come naturally when we start counting. In mathematics, counting numbers are called natural numbers.
What can we count? Everything: the number of family members, the number of fingers, the number of spectators in the theatre, the number of houses in the city. Does this seem impossible to you? Yes, it is hard to count all houses in the city, but if you know how many houses there are at the moment, then when a new house appears, you will also know how many houses there are in the city. However, sometimes it is very-very difficult to count what we are interested in. For example, the number of cat hairs. But there would be some number describing the number of cat’s hairs. And there will also be a number that describes the number of one more hair or two more hairs and so on. So, the smallest natural number is number 1 and there is no largest natural number.
If we add the number 0 to the set of natural numbers, we get the set of whole numbers. This can be very clearly illustrated in the following diagram.

Therefore, every natural number is a whole number, and every non-zero whole number is a natural number. Sets of whole numbers and natural numbers differ by only one number – by 0.
Why did it happen with zero that it is separated from the set of natural numbers? Surprisingly, but zero appeared millennia after the appearance of natural numbers. Only in ancient India they realized that “nothing could be something” and denoted “this nothing” as zero.
How to identify a whole number?
Here are three basic rules helping to determine whether a number is a whole number or not:
- A whole number is never a negative number. This means that it has to be of a value of 0 or higher. For example, 0, 1, 2, 3, 4… are all whole numbers, however, -1, -2, -3, -4, … are not whole numbers.
- A whole number is never a fractional number. This means that numbers like $\frac{3}{4}, \frac{15}{7}, 1\frac{1}{2}$,… are not whole numbers.
- A whole number is never a decimal number. This means that numbers such as 0.1, 1.2, 100.008 are not whole numbers.
If you are dealing with rational numbers and these numbers meet the three described requirements, then you can be sure your number is a whole number.
EXAMPLE: 15, -6, $\frac{2}{9}$, 10001, 14.5, 31234532.
Write the numbers in the table below. Explain each step.
| Whole numbers | Not whole numbers |
SOLUTION: Start with the first number. Number 15 is not negative, fractional or decimal, so it is a whole number as well as numbers 10001 and 31234532.
Number -6 is not a whole number because it is negative number. Number $\frac{2}{9}$ is not a whole number as it is a fractional number. Number 14.5 is not a whole number because it is a decimal.
| Whole numbers | Not whole numbers |
| 15, | -6, |
| 10001, | 29, |
| 31234532 | 14.5 |
Number line
Number line helps us to represent whole numbers (and further other numbers), visualize number sequences and demonstrate strategies for counting and arithmetic. A number line is a straight line (usually horizontal) with numbers placed at equal intervals along this line.
How can we draw a number line? Draw a line and mark a point on it. Label this point with the first whole number 0. Mark a second point to the right of 0 and label it with the next whole number 1. The distance between these two whole numbers is called unit distance on the number line. Continue placing whole numbers on the number line in the same way: mark the next point on the unit distance to the right of 1 and label it with the number 2, and so on. Using the described algorithm, we can denote any whole number on a number line.

Each whole number can be identified with the number of unit distances we have to cover starting at 0 and moving to that number. So, number 4 can be represented as 4 unit distances as we need to make “4 unit steps” to get from 0 to number 4 (see diagram below).

After learning the other numbers, you will know how to place them on a number line, but for now we will limit ourselves to whole numbers.
The numbers on the number line increase if we move from left to right and decrease when we move from right to left. Out of any two whole numbers, the number on the right of the other number is the greater number and the number on the left of the other number is the smaller number. For example, from the above diagram we can see that number 10 is to the right of number 6, so 10>6 and number 7 is to the left of number 12, so number 7<12. This helps us to order whole numbers.
Now, what is the distance between two whole numbers 4 and 6? On a number line, the distance between two neighbour numbers is always a unit distance 1. So, each distance between 4 and 5 and between 5 and 6 is equal to one unit distance. Hence, the distance between two whole numbers 4 and 6 is 2 unit distances or simply 2. In the same way, we can count the distance between arbitrary two whole numbers.
Arithmetic operations on a number line
ADDITION: To add one whole number to another whole number, we must move from the first number to the right by as many unit distances as the second number represents.
EXAMPLE: Using number line, add 5+3.
SOLUTION: Step 1: Draw a number line with whole numbers and find the first number 5 on it.

Step 2: Represent the second number 3 as three unit distances.
Step 3: Move 3 unit distances to the right from number 5, you get to number 8.

This means 5+3=8.
By the way, you can see that addition is commutative operation changing the order of numbers in previous example. So, the following number line shows why 3+5=8 too.

SUBTRACTION: To subtract two whole numbers, we move to the left of the greater number by the number of unit distances, which represents the smaller number.
EXAMPLE: Using number line, subtract 9-6.
SOLUTION: Step 1: Draw a number line with whole numbers and find the greater number 9 on it.

Step 2: Represent the second number 6 as six unit distances.
Step 3: Move 6 unit distances to the left from number 9, you get to number 3.

This means 9-6=3.
In fact, there are some complications with subtracting numbers, as the difference between two whole numbers can sometimes be non-whole number. For example, 100-200 is not a whole number. Therefore, subtraction is not a closed operation on a set of whole numbers.
MULTIPLICATION: To multiply a whole number a by a whole number b, we need to take a times b unit distances.
EXAMPLE: Using number line, multiply 3×4.
SOLUTION: Step 1: Draw a number line with whole numbers and start from 0.

Step 2: Move to the right 4 units (the length of the “step” is equal to the second number).
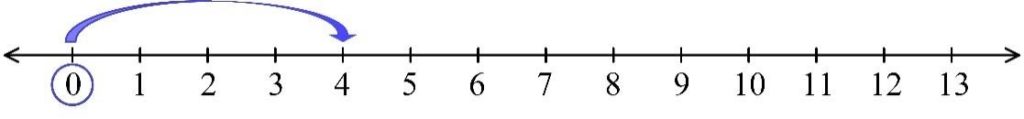
Step 3: Make from zero to the right 3 such “steps” (the number of steps is equal to the first number).

This means 3×4=12.
As with addition, for multiplication it is also easy to see that the product of two whole numbers is commutative. So, the following number line shows why 4×3=12 too.

Let’s start with the fact that division on a set of whole numbers is not a closed operation. The result of division two whole numbers is much more often a non-whole number than it is. Therefore, the division of whole numbers on a number line is used in rare cases.
DIVISION: To divide whole number a by whole number b, start from number a and find how many steps of length b you should move to the left to get to 0.
EXAMPLE: Using number line, divide 10÷2.
SOLUTION: Step 1: Draw a number line with whole numbers and start from 10.

Step 2: Move to the left 2 units (the length of the “step” is equal to the second number).
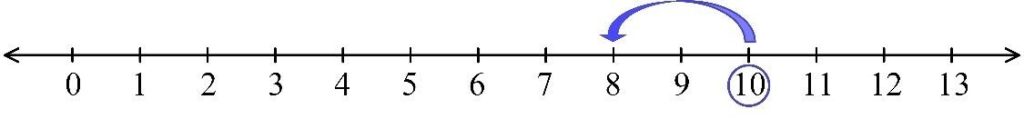
Step 3: Make from number 10 to the left 5 such “steps” (the number of steps is equal to the quotient).

This means 10÷2=5.
Properties of whole numbers
Examining arithmetic operations with whole numbers in more detail, we can see that these operations have certain properties. Some of these properties allow us to determine whether or not to do operations with whole numbers, and some properties help us to make calculations simpler. Consider the basic properties of numbers and find out which operations have these properties and which do not have.
Denote the operation on the set of whole numbers by the symbol *.
CLOSURE PROPERTY: An operation is said to be closed on a set of whole numbers if the result of this operation belongs to the set of whole numbers.
If a and b are two whole numbers, then a*b is a whole number too.
As we discussed earlier, subtraction and division are not closed operations. Addition and multiplication are closed operations on the set of whole numbers as the sum of whole numbers and the product of whole numbers are always whole numbers.
COMMUTATIVE PROPERTY: An operation is said to be commutative on a set of whole numbers if when we change the order of operation, the result remains unchanged.
If a and b are two whole numbers, then a*b=b*a.
This property also holds true for multiplication, but not for subtraction or division.
ASSOCIATIVE PROPERTY: An operation is said to be associative on a set of whole numbers if you can rearrange the parentheses without rearranging the numbers and the result remains the same.
If a, b and c are three whole numbers, then (a*b)*c=a*(b*c).
Subtraction and division of whole numbers are not associative operations. Let us illustrate this by the following examples.
Subtraction: 12-6-4=6-4=2 but 12-6-4=12-2=10 (here two results are not the same)
Division: 8÷4÷2=2÷2=1 but 8÷4÷2=8÷2=4 (two results are not the same again)
Addition and multiplication of whole numbers are associative operations on the set of whole numbers.
DISTRIBUTIVE PROPERTY: when we multiply the sum of two or more numbers by a third number, then it will give same result as multiplying each number individually by the number and then adding each of the multiplication results.
If a, b and c are three whole numbers, then a+b×c=a×c+b×c.
Since addition and multiplication are commutative operations, the following equality is also true.
c×a+b=c×a+c×b
For example, 4+7×5=11×5=55 and 4×5+7×5=20+35=55. So, we can calculate the result of 4+7×5 using the distributive property in two different ways, adding and multiplying or multiplying, multiplying and then adding. In each case, it is worth looking at how best to count.
ADDITIVE IDENTITY: The set is said to have an additive identity if the sum of any number from the set and this additive identity is the number itself. Usually, we denote additive identity as 0.
If a is a whole number, then a+0=0+a=a.
The additive identity for whole numbers is a whole number 0 i.e on adding 0, the number remains unchanged.
MULTIPLICATIVE IDENTITY: The set is said to have a multiplicative identity if the product of any number from the set and this multiplicative identity is the number itself. Usually, we denote multiplicative identity as 1.
If a is a whole number, then a×1=1×a=a.
The multiplicative identity for whole numbers is a whole number 1 i.e multiplying by 1, the number remains unchanged.
MULTIPLICATION BY ZERO: When a whole number is multiplied to 0, the result is always 0.
If a is a whole number, then a×0=0×a=0
It should be noted that there is one property that none of the arithmetic operations has this property on the set of whole numbers.
INVERSE PROPERTY: A set has the inverse property under an arithmetic operation if every element of the set has an inverse element. An inverse of an element is another element in the set that, when combined on the right or the left through the operation, always gives the identity element as the result. An inverse under addition to element a usually is denoted as -a.
If a is a number, then a+(-a)=(-a_+a=0
An inverse under multiplication to element a usually is denoted as a-1.
If a is a number, then a×a-1=a-1×a=1
Let us illustrate why addition and multiplication do not have inverse property.
Addition: There is no such whole number that can be added, for example, to 10 to get additive identity 0.
Multiplication: There is no such whole number that, for example, 10 can be multiplied by to get multiplicative identity 1.
DIVISION BY ZERO: Division of a whole number by 0 is not defined.
If x is a whole number then $\frac{x}{0}$ is not defined
If the properties hold for some arithmetic operations on the set, then they can be combined and we can see how to get easier calculations. For example, (5×13)×2 is easier to calculate using commutative and associative properties of multiplication. First, change the order of numbers in the parentheses (apply commutative property):
(5×13)×2=(13×5)×2
Now, change the order of parentheses (apply associative property):
(5×13)×2=(13×5)×2=13×(5×2)
In the parentheses we have 5×2 that is 10 and multiplication by 10 is the easiest one, so
(5×13)×2=(13×5)×2=13×(5×2)=13×10=130
Other numbers
Mathematicians are inquisitive people, and in working with whole numbers’ properties they wanted to expand the set of whole numbers that as many properties as possible were satisfied. For example, to make the inverse property under addition true, they came up with negative numbers. So, we can deal with a set of integers and it is easy to determine the inverse number under the addition. For example, the inverse under the addition of whole number 10 will be integer -10. Making the inverse property under multiplication true, they came up with fractional numbers. So, we can deal with a set of rational numbers and it is easy to determine the inverse number under the multiplication. For example, the inverse under the multiplication of whole number 10 will be fraction 110. Considering other (not listed here) properties, mathematicians denoted irrational, real and complex numbers. Interested in other numbers? Read more about rational, irrational and complex numbers.
Quiz
- In each statement, change one word to get the correct statement.
a) Zero is the smallest natural number.
b) Zero is the largest whole number.
c) We can subtract whole numbers in any order.
d) If the product of two whole numbers is zero, then first of the numbers is zero.
SOLUTION: a) Zero is not a natural number at all. Zero is the smallest whole number. So, in the statement “Zero is the smallest natural number” change word “natural” for “whole” and then statement “Zero is the smallest whole number” becomes true.
b) We know there is no largest whole number. Also, we know that zero is the smallest whole number. So, change word “largest” for “smallest” to get correct statement “Zero is the smallest whole number”.
c) Subtraction is not a commutative operation. From the article we know that addition and multiplication are commutative operations, so if we change word “subtract” for “add” or “multiply” we will obtain the correct statement “We can add (multiply) whole numbers in any order”.
d) If the product of two whole numbers is zero, not only the first of the numbers could be zero. If the second number in product is zero, then the product equals to zero to. So, change the word “first” for “one” to make statement “If the product of two whole numbers is zero, then one of the numbers is zero”.
- What arithmetic operation is illustrated on the numerical line?

SOLUTION: We start with 13 and move 7 unit distances to the left, so we decrease 17 by 7 to get 6. This is subtraction and the number line illustrates
13-7=6
ANSWER: 13-7=6
- Perform the calculations in the most convenient way. Explain your reasoning.
a) 343×47+47×657;
b) 852 + 717 + 1283 + 148;
c) (125 × 489) × 32.
SOLUTION: a) First, apply commutative property of multiplication:
343×47+47×657=47343+47×657
Now, use distributive property:
47×343+47×657=47×(343+657)
At last, it is easy to calculate that 343+657=1000, then
47×343+657=47×1000=47000
b) First, use commutative property of addition:
852 + 717 + 1283 + 148=1283 + 717 + 852 + 148
Add first two numbers and last to numbers:
1283+717=2000
852+148=1000
So,
1283 + 717 + 852 + 148=2000+1000=3000
c) Apply commutative property of multiplication:
125 × 489× 32=(489 × 125)× 32
Now, use multiplicative associativity:
489 × 125× 32=489 ×(125× 32)
Since 125×32=4000, then
489 ×125× 32=489×4000=1956000
ANSWER: a) 47000 b) 3000 c) 1956000
- Which of the following will not represent 12? Explain why.
a) 12+0;
b) 12-12+12;
c) 1+12;
d) 12÷1.
SOLUTION: Complete all calculations.
a) 0 is additive identity, so
12+0=12
b) Since 12-12=0 and 0 is additive identity, we have that
(12-12)+12=0+12=12
c) 1 is multiplicative identity, 12×1=12, not additive identity,
12+1=13≠12
d) Division by 1 never changes the number as we move to the left in “unit steps”,
12÷1=12
ANSWER: c)
- Which of the following will not represent 0? Explain why.
(There could be more than one correct answer)
a) 13×0;
b) 13+0;
c) 0/13;
d) 13/0.
SOLUTION: a) Multiplication by 0 property says that
13×0=0
b) 0 is additive identity, so
13+0=13≠0
c) When we divide “nothing”, we get “nothing” too, so
0/13=0
d) Division by 0 is not allowed, 13/0 is undefined.
ANSWER: b) and d)
Conclusions
- Each natural number is a whole number.
- Each non-zero whole number is a natural number.
- The smallest whole number is 0.
- There is no the largest whole number.
- There is a range of properties of whole numbers, but also there are properties that do not hold.
Recommended Worksheets
Basic Operations of Whole Numbers (All Saints’ Day Themed) Math Worksheets
Rounding Whole Numbers (Tens and Hundreds) (Sea Animals Themed) Worksheets
Rounding Whole Numbers and Decimals (Basketball Themed) Worksheets









