Introduction
You plot ordered pairs on the Cartesian plane, also known as the x-y plane, which is a two-line graph. Four distinct quadrants are created by the two intersecting lines of the Cartesian plane. A quadrant is a region bounded by the intersection of the x – axis and the y – axis.
We will learn more about the four quadrants of a coordinate system in this article, as well as how to plot and locate points in each quadrant.
The Four Quadrants
The rectangle coordinate system is split into four equal parts by the intersection of the x – axis and the y – axis. The x – axis is the horizontal number line, while the y – axis is the vertical number line.
As shown below, the coordinate system has four regions representing one-quarter of the entire coordinate system. Each quadrant has its properties and is frequently labeled using Roman numerals.
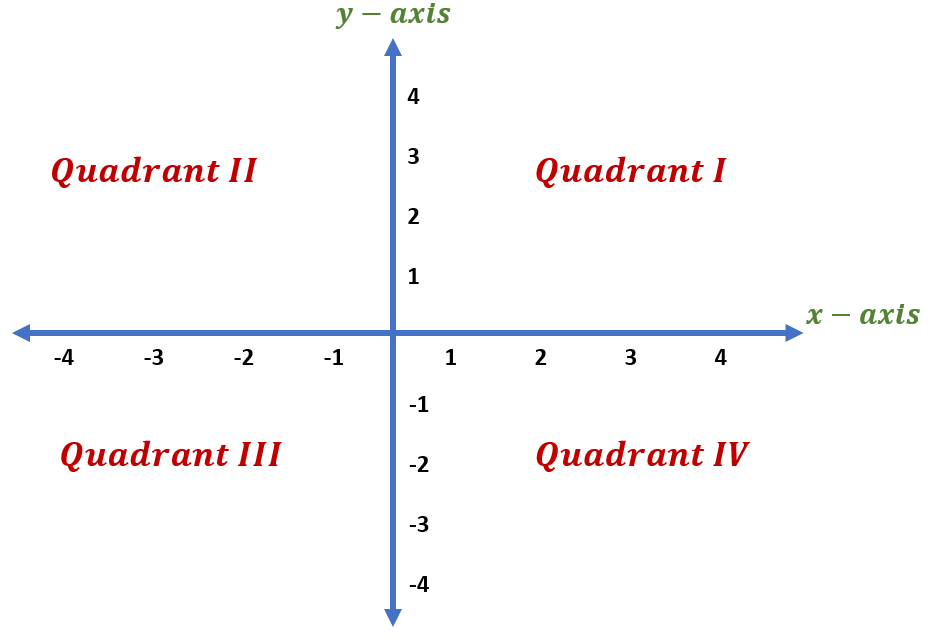
The movement of the label from Quadrant I to IV follows an anti-clockwise rotation starting from the upper right quadrant to the bottom right quadrant.
Quadrant I, or the first quadrant, is the upper right quadrant. Both the x – axis and y – axis have positive numbers in Quadrant I.
Quadrant II, or the second quadrant, is the upper left quadrant. In Quadrant II, the x – axis has negative numbers while the y – axis has positive numbers.
Quadrant III, or the third quadrant, is the bottom left quadrant. Both the x – axis and y – axis have negative numbers in Quadrant III.
Quadrant IV, or the fourth quadrant, is the bottom right quadrant. In Quadrant IV, the x – axis has positive numbers while the y – axis has negative numbers.
Points on the Quadrants
The location of a point has something to do with its vertical distance from the x – axis and its horizontal distance from the y – axis. The intersection of the two axes, the x- and y – axis, is known as the origin, which is point ( 0, 0 ).
Let us say, for example, in the illustration below, we have point M, and we want to identify its location in the coordinate system. To find the location of point M, let us draw two straight lines starting from this point. One line is horizontal towards the y – axis, while the other is vertical towards the x – axis.
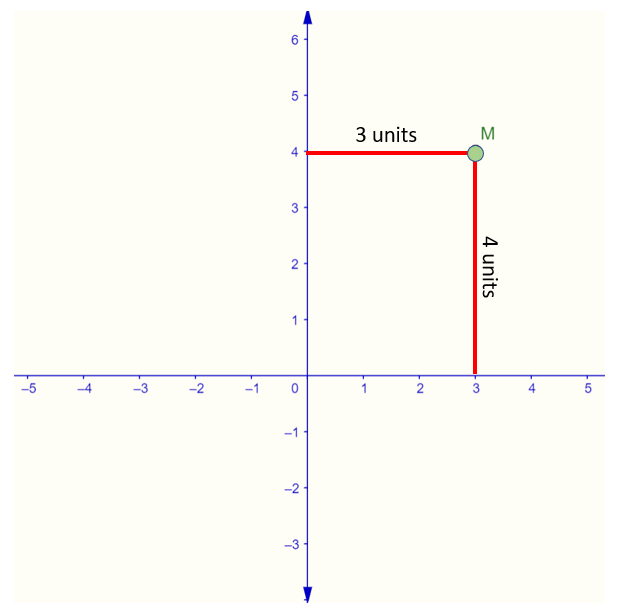
The location of point M is 3 units on the x – axis while 4 units on the y – axis. Therefore, the location of point M using an ordered pair is ( 3, 4 ), or we may also say M ( 3, 4 ).
The points on the coordinate system are always written in the form ( x, y ), in which x is referred to as the abscissa, and y is called the ordinate.
As for another example, in the figure below, let us locate point K in the coordinate system. To find the location of point K, let us draw two straight lines starting from this point. One line is horizontal towards the y – axis, while the other is vertical towards the x – axis.

The location of point K is 2 units on the x – axis while 1 unit on the y – axis. Therefore, the location of point K using an ordered pair is ( 2, -1 ), or we may also say K ( 2, -1 ).
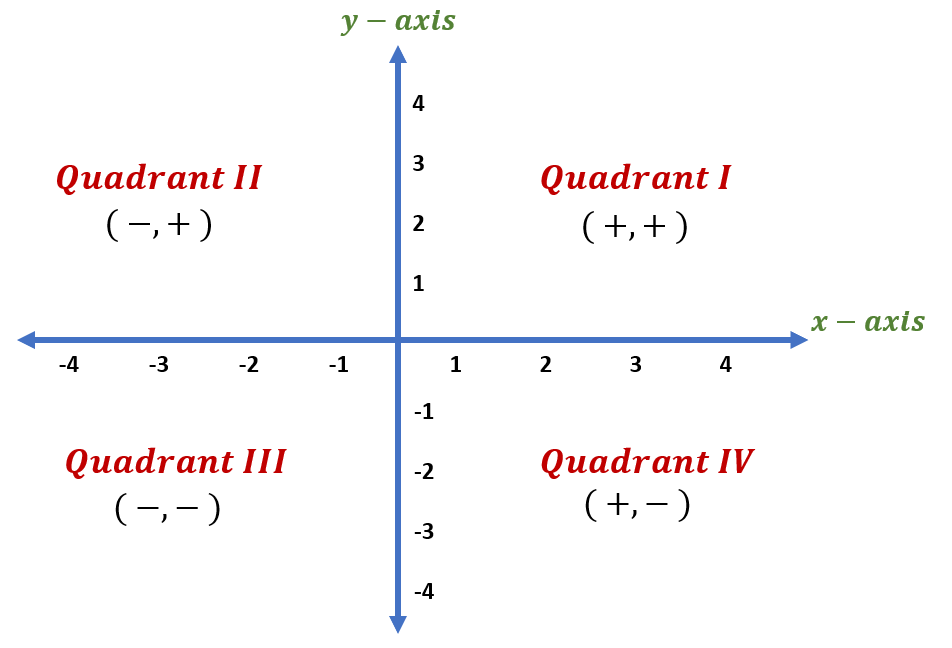
Signs of the Coordinates in Quadrants
There are four different quadrants, depending on the sign of the coordinates. To identify which quadrant the point is in, you must know the ordinate and abscissa signs of an ordered pair.
The signs of the coordinates for each quadrant
are displayed in the table below.
| Quadrant | Abscissa | Ordinate | Signs of the Coordinates |
| I | positive | positive | ( + , + ) |
| II | negative | positive | ( – , + ) |
| III | negative | negative | ( – , – ) |
| IV | positive | negative | ( + , – ) |
Plotting Points on the Coordinate System
In plotting points on the coordinate system, you must be mindful of the signs of the x-coordinate and the y-coordinate. Remember also that the intersection of the two axes, x and y, is the origin ( 0, 0 ).
Let us say, for example, we want to plot point Z with coordinates ( -2, 3 ). Since the x-coordinate is negative 2, let us move 2 units to the left starting from the origin.
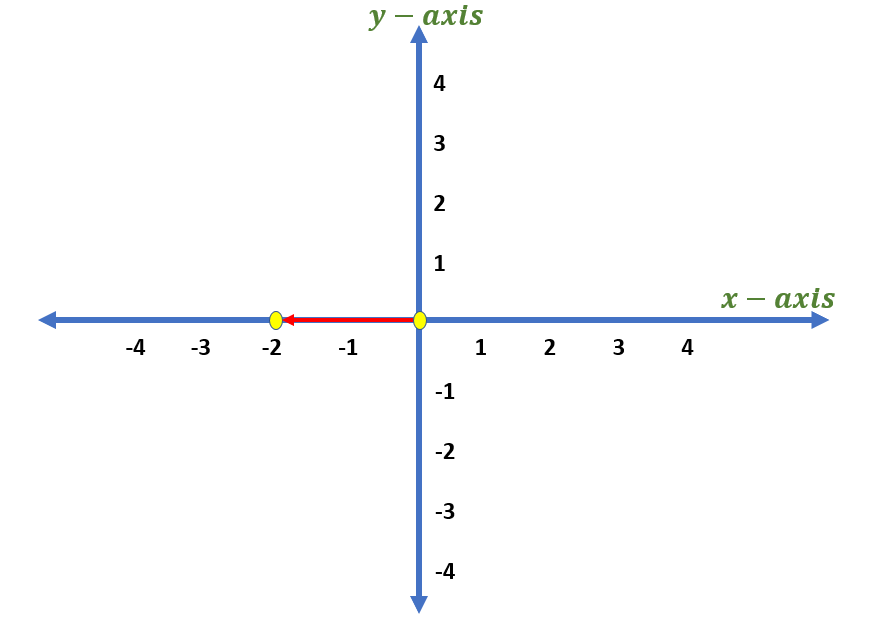
Since the y-coordinate is positive 3, we will move 3 units upward. As shown below, point Z is in Quadrant II.

As for another example, let us plot point H with coordinate ( 3, -3 ). Since the x-coordinate is positive, we will move 3 units to the right starting from the origin. Then, move 3 units down since the y-coordinate is negative 3. The figure below shows that H ( 3, -3 ) is in Quadrant IV.
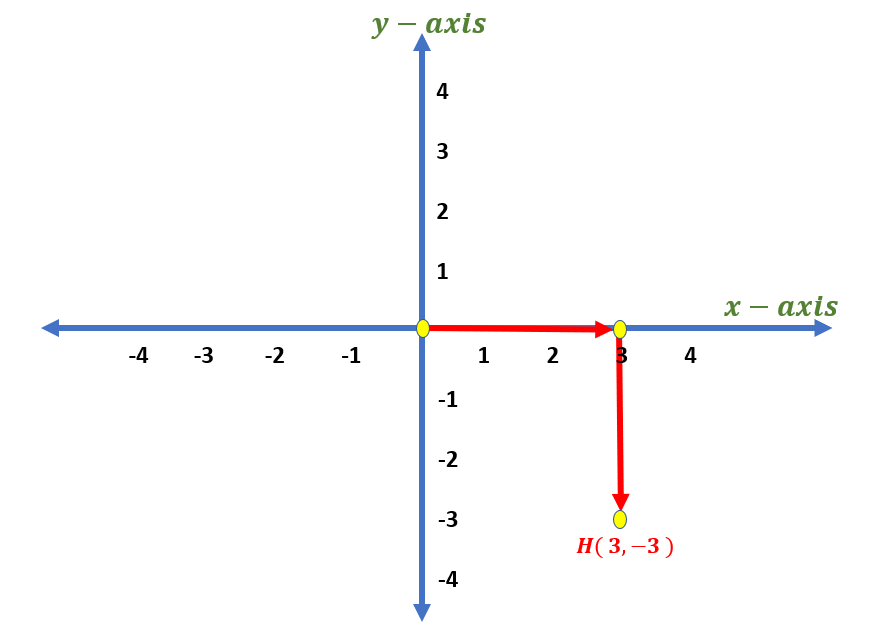
Examples
Example 1
Determine the quadrant in which each point is located.
( a ) ( 5, 8 )
( b ) ( -9, 12 )
( c ) ( 20, -16 )
( d ) ( -3, -10 )
( e ) ( -4, 11 )
( f ) ( 12, -5 )
Solution
( a ) ( 5, 8 )
Since the x-coordinate and the y-coordinate are both positive, ( 5, 8 ) is in Quadrant I.
( b ) ( -9, 12 )
Since the x-coordinate is negative and the y-coordinate is positive, ( -9, 12 ) is in Quadrant II.
( c ) ( 20, -16 )
Since the x-coordinate is positive and the y-coordinate is negative, ( 20, -16 ) is in Quadrant IV.
( d ) ( -3, -10 )
Both the x-coordinate and the y-coordinate are negative; hence, ( -3, -10 ) is in Quadrant III.
( e ) ( -4, 11 )
Since the x-coordinate is negative and the y-coordinate is positive, ( -4, 11 ) is in Quadrant II.
( f ) ( 12, -5 )
Since the x-coordinate is positive and the y-coordinate is negative, ( 12, -5 ) is in Quadrant IV.
Example 2
Plot the following points in a coordinate system and note which quadrant each one is in.
( a ) A ( 1, 5 )
( b ) B ( 2, -3 )
( c ) C ( -4, -1 )
( d ) D ( -1, 3 )
( e ) E ( 5, 4 )
Solution
The graph below shows the location of each point.
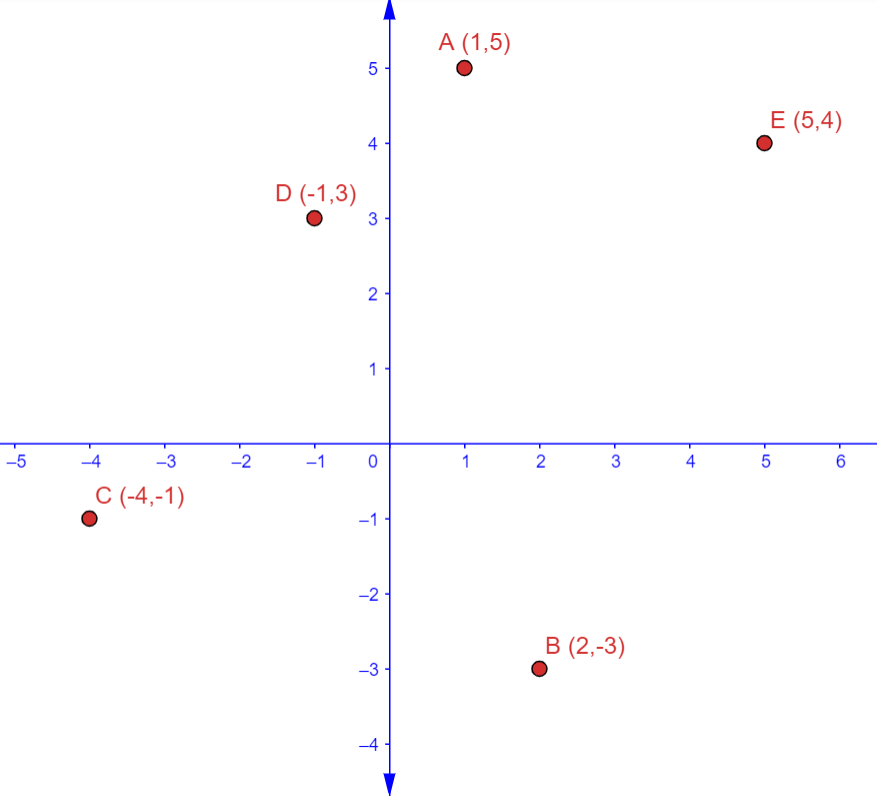
( a ) A ( 1, 5 )
Since both the x-coordinate and the y-coordinate are positive, point A is in Quadrant I.
( b ) B ( 2, -3 )
Since the x-coordinate is positive while the y-coordinate is negative, point B is in Quadrant IV.
( c ) C ( -4, -1 )
Both the x-coordinate and the y-coordinate are negative. Hence, point C is in Quadrant III.
( d ) D ( -1, 3 )
Since the x-coordinate is negative and the y – coordinate is positive, point D is in Quadrant II.
( e ) E ( 5, 4 )
Since both the x-coordinate and the y-coordinate are positive, point E is in Quadrant I.
Example 3
Which points below lie in the third quadrant or QIII?
L ( -3, 9 )
M ( -4, -8 )
N ( 9, -8 )
O ( -10, 25 )
P ( -12, -17 )
Q ( 4, 15 )
Solution
The points in the third quadrant or QIII must have both negative x- and y-coordinates. Therefore, points M ( -4, -8 ) and P ( -12, -17) are in QIII.
On the other hand, points L ( -3, 9 ) and O ( -10, 25 ) are in Quadrant II, point N ( 9, -8 ) is in Quadrant IV, and point Q ( 4, 15 ) is in Quadrant I.
Example 4
Where does each point lie in the coordinate system’s four quadrants?
( a ) P ( 2, 0 )
( b ) Q ( 0, -4 )
( c ) R ( -6, 0 )
( d ) S ( 0, 7 )
( e ) S ( 5, 0 )
Solution
( a ) P ( 2, 0 )
Starting from the origin, point P with coordinates ( 2, 0 ) is 2 units to the right. It does not lie in any of the four quadrants. Point P ( 2, 0 ) is along the positive x – axis.
( b ) Q ( 0, -4 )
Starting from the origin, point Q with coordinates ( 0, -4 ) is 4 units downward. It does not lie in any of the four quadrants. Point Q ( 0, -4 ) is along the negative y – axis.
( c ) R ( -6, 0 )
Starting from the origin, point R with coordinates ( -6, 0 ) is 6 units to the left. It does not lie in any of the four quadrants. Point R ( -6, 0 ) is along the negative x – axis.
( d ) S ( 0, 7 )
Starting from the origin, point S with coordinates ( 0, 7 ) is 7 units upward. It does not lie in any of the four quadrants. Point S ( 0, 7 ) is along the positive y – axis.
( e ) P ( 5, 0 )
Starting from the origin, point P with coordinates ( 2, 0 ) is 5 units to the right. It does not lie in any of the four quadrants. Point P ( 5, 0 ) is along the positive x – axis.
Example 5
Give 5 examples of points in each quadrant in a coordinate system.
Solution
In Quadrant I, both x – coordinate and y – coordinate must be positive; hence, the following are some examples: ( 1, 2 ). ( 4, 8 ), ( 16, 78 ), ( 3, 7 ), and ( 100, 1000 ).
In Quadrant II, the x – coordinate is negative while the y – coordinate is positive; thus, some examples are ( -8, 9 ). ( -6, 10 ), ( -21, 18 ), ( -3, 15 ), and ( -25, 100 ).
In Quadrant III, both x – coordinate and y – coordinate must be negative; hence, the following examples are ( -6, -21 ). ( -13, -5 ), ( -2, -1 ), ( -4, -18 ), and ( -100, -8 ).
In Quadrant IV, the x – coordinate is positive while the y – coordinate is negative; thus, some examples are ( 9, -8 ). ( 21, -6 ), ( 4, -1 ), ( 11, -12 ), and ( 19, -5 ).
Example 6
In which quadrant does ( x, 3 ) lie?
Solution
Since ( x, 3 ) does not indicate a definite x – coordinate, it means that x is a collection of positive or negative numbers. If we try to plot it in the coordinate system, it forms a horizontal at y = 3.
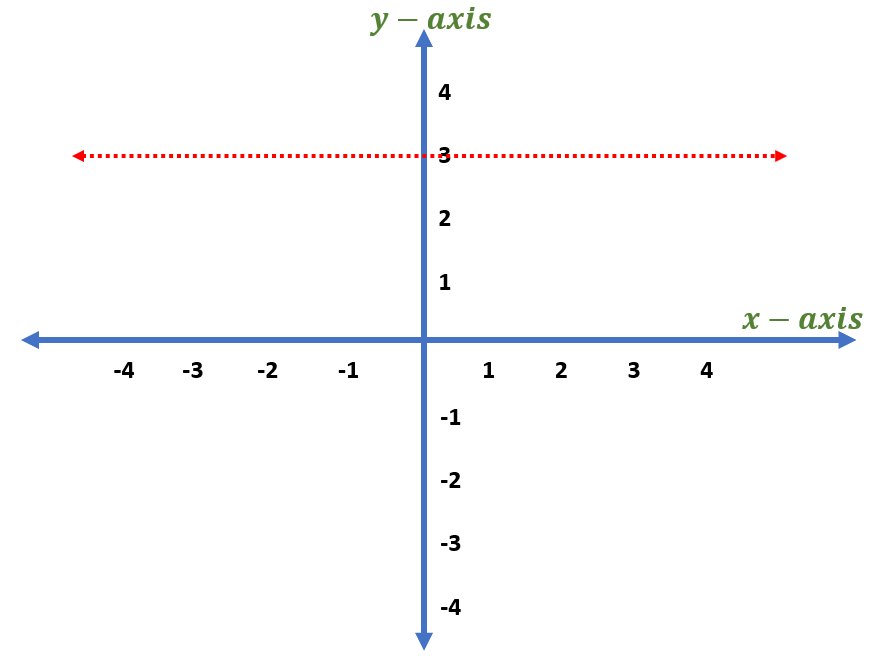
Therefore, we can say that the quadrants are QI and QII.
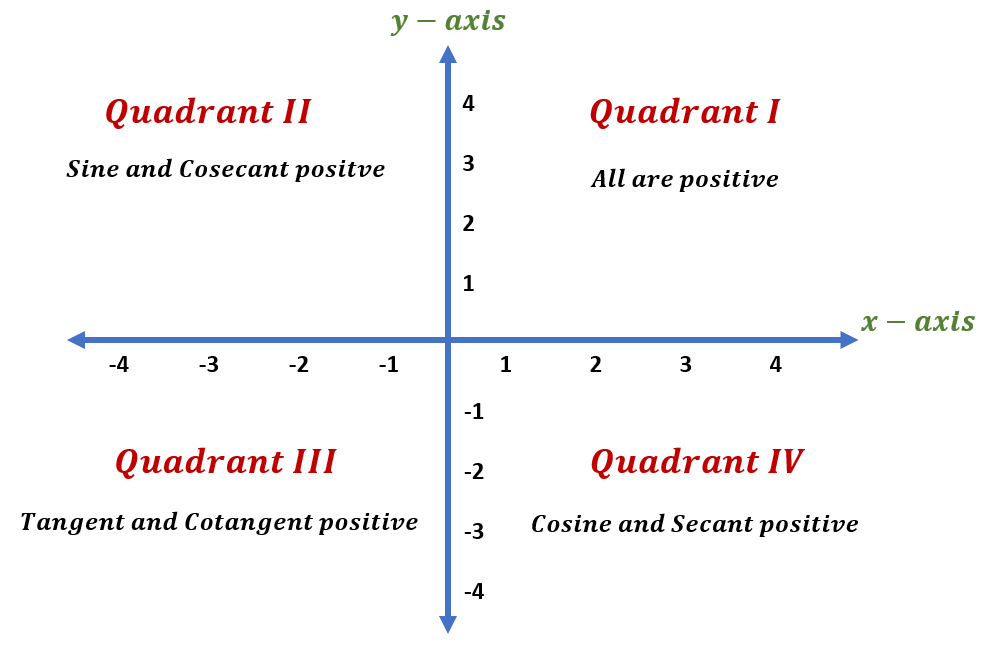
Trigonometric Functions in Quadrants
A trigonometric function’s sign is determined by the signs of the x and y – coordinates of the points on the angle’s terminal side. You can determine the signs of all the trigonometric functions by determining which quadrant an angle’s terminal side is located.
All six trigonometric functions are positive in the first quadrant or Quadrant I since both x- and y – coordinates are positive.
In the second quadrant or Quadrant II, since y – coordinate is positive and x – coordinate is negative, only sine and cosecant are positive.
In the third quadrant or Quadrant III, since both x- coordinate and y – coordinate are negative, only tangent and cotangent are positive.
In the fourth quadrant or QIV, since x – coordinate is positive and y – coordinate is negative, only cosine and cosecant are positive.
The chart below illustrates the trigonometric functions that are positive in each quadrant.
Summary
The rectangle coordinate system is split into four equal parts by the intersection of the x – axis and the y – axis. The x – axis is the horizontal number line, while the y – axis is the vertical number line.
Each one-quarter region of the entire coordinate system is a quadrant. The quadrants are called the first quadrant ( QI ), second quadrant ( QII ), third quadrant ( QIII ), and fourth quadrant ( QIV ).
The signs of the coordinates for each quadrant are displayed in the table below.
| Quadrant | Signs of the coordinates |
| I | ( + , + ) |
| II | ( – , + ) |
| III | ( – , – ) |
| IV | ( + , – ) |
Angles in Each Quadrant
The angles in the first quadrant or QI lie between 0° and 90°.
The angles in the second quadrant or QII lie between 90° and 180°.
The angles in the third quadrant or QIII lie between 180° and 270°.
The angles in the fourth quadrant or QIV lie between 270° and 360°.
The signs of the six trigonometric functions in each quadrant are displayed in the table below.
| TrigonometricFunction | Quadrants | |||
| I | II | III | IV | |
| sin | positive | positive | negative | negative |
| cos | positive | negative | negative | positive |
| tan | positive | negative | positive | negative |
| cot | positive | negative | positive | negative |
| sec | positive | negative | negative | positive |
| csc | positive | positive | negative | negative |
Frequently Asked Questions on All Four Quadrants ( FAQs )
What is meant by quadrants in a coordinate system?
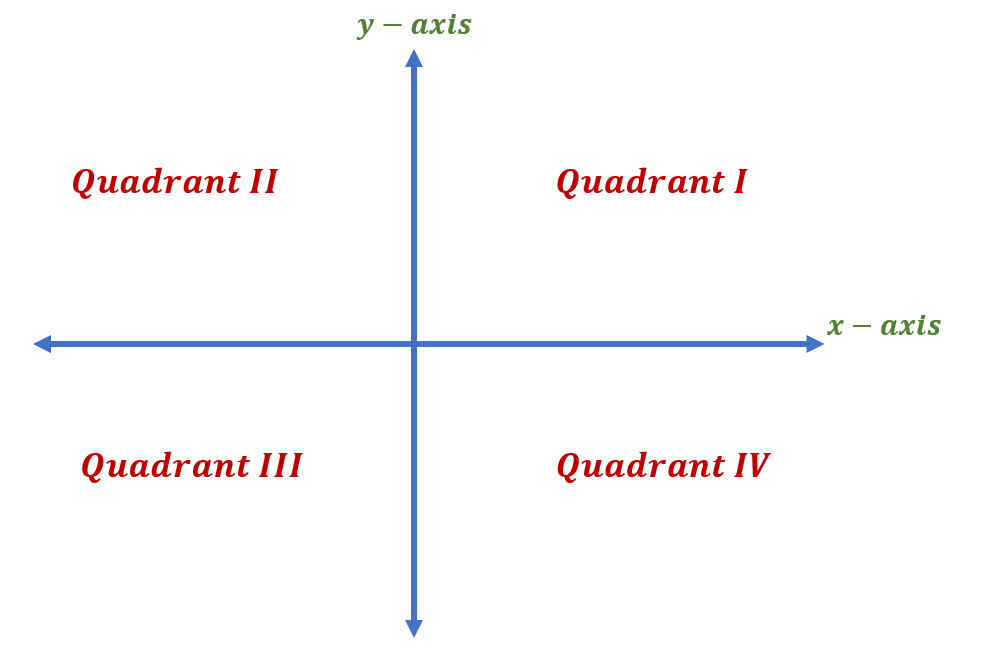
The rectangle coordinate system is split into four equal parts by the intersection of the x – axis and the y – axis. The x – axis is the horizontal number line, while the y – axis is the vertical number line. Each one-quarter region of the entire coordinate system is a quadrant. The quadrants are called the first quadrant ( QI ), second quadrant ( QII ), third quadrant ( QIII ), and fourth quadrant ( QIV ).
The image below shows the four quadrants in a coordinate system.
What is a coordinate system?
Any point can be located using a Cartesian coordinate system or coordinate system, and that point can be displayed as an ordered pair (x, y). The x and y are known as the coordinates of the ordered pair. The origin, indicated by the letter “O,” is the place where the two number lines intersect. The horizontal number line is known as the x – axis, while the vertical number line is known as the y – axis.
Where is the origin in the coordinate system?
The coordinates coordinate system’s origin is the intersection of the x – and y – axis. It is point ( 0, 0 ) as an ordered pair.
How do you identify the quadrant of a point?
A coordinate system has four quadrants. Each quadrant has its properties and is frequently labeled using Roman numerals.
Quadrant I, or the first quadrant, is the upper right quadrant. Both the x – axis and y – axis have positive numbers in Quadrant I.
Quadrant II, or the second quadrant, is the upper left quadrant. In Quadrant II, the x – axis has negative numbers while the y – axis has positive numbers.
Quadrant III, or the third quadrant, is the bottom left quadrant. Both the x – axis and y – axis have negative numbers in Quadrant III.
Quadrant IV, or the fourth quadrant, is the bottom right quadrant. In Quadrant IV, the x – axis has positive numbers while the y – axis has negative numbers.
| Quadrant | x- coordinate | y-coordinate | Ordered Pair |
| I | Positive | Positive | ( + , + ) |
| II | Negative | Positive | ( – , + ) |
| III | Negative | Negative | ( – , – ) |
| IV | Positive | Negative | ( + , – ) |
The signs of the coordinates for each quadrant are displayed in the table below.
What are the measures of the angles in each quadrant?
The coordinate system is split into four quadrants, I, II, III, and IV. If we are referring to angles in standard position, they have different measures depending on the location of the terminal side in the coordinate system.
As shown below, 0°, 90°, 180°, 270°, and 360° lie along the axes, and they are considered as quadrantal angles. Note that the labels below are for angles in standard position with positive rotations.
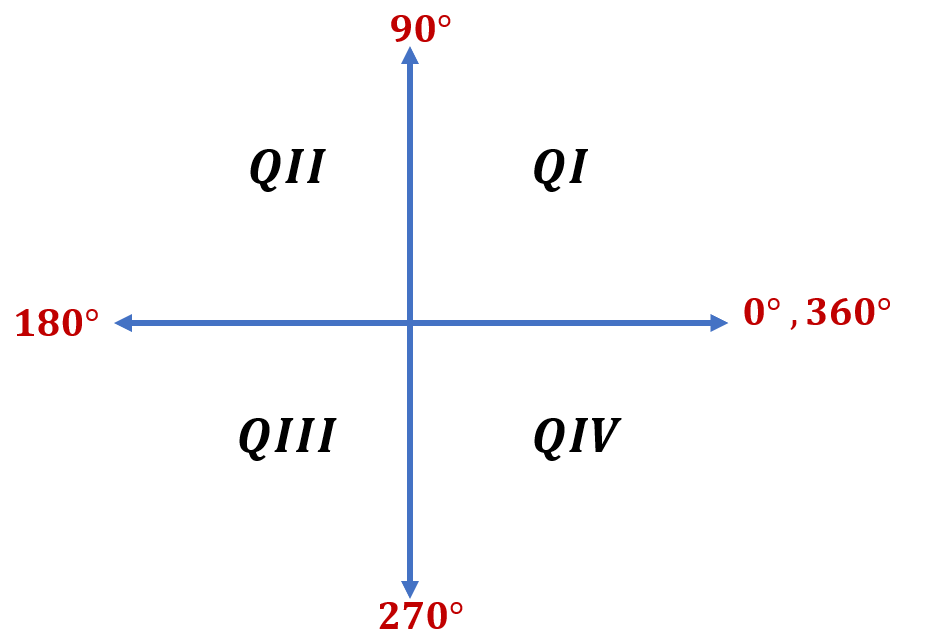
The angles in the first quadrant or QI lie between 0° and 90°.
The angles in the second quadrant or QII lie between 90° and 180°.
The angles in the third quadrant or QIII lie between 180° and 270°.
The angles in the fourth quadrant or QIV lie between 270° and 360°.
What are the sign conventions for the coordinates in quadrants?
The signs of the coordinates for each quadrant are displayed in the table below.
| Quadrant | Signs of the Coordinates |
| I | ( + , + ) |
| II | ( – , + ) |
| III | ( – , – ) |
| IV | ( + , – ) |
What are the trigonometric values in each quadrant?
All six trigonometric functions are positive in the first quadrant or Quadrant I since both x- and y – coordinates are positive.
In the second quadrant or Quadrant II, since y – coordinate is positive and x – coordinate is negative, only sine and cosecant are positive.
In the third quadrant or Quadrant III, since both x- coordinate and y – coordinate are negative, only tangent and cotangent are positive.
In the fourth quadrant or QIV, since x – coordinate is positive and y – coordinate is negative, only cosine and cosecant are positive.
The signs of the six trigonometric functions in each quadrant are displayed in the table below.
| TrigonometricFunction | Quadrants | |||
| I | II | III | IV | |
| sin | positive | positive | negative | negative |
| cos | positive | negative | negative | positive |
| tan | positive | negative | positive | negative |
| cot | positive | negative | positive | negative |
| sec | positive | negative | negative | positive |
| csc | positive | positive | negative | negative |
What are all four quadrants in order?
The movement of the label from Quadrant I to IV follows an anti-clockwise rotation starting from the upper right quadrant to the bottom right quadrant.
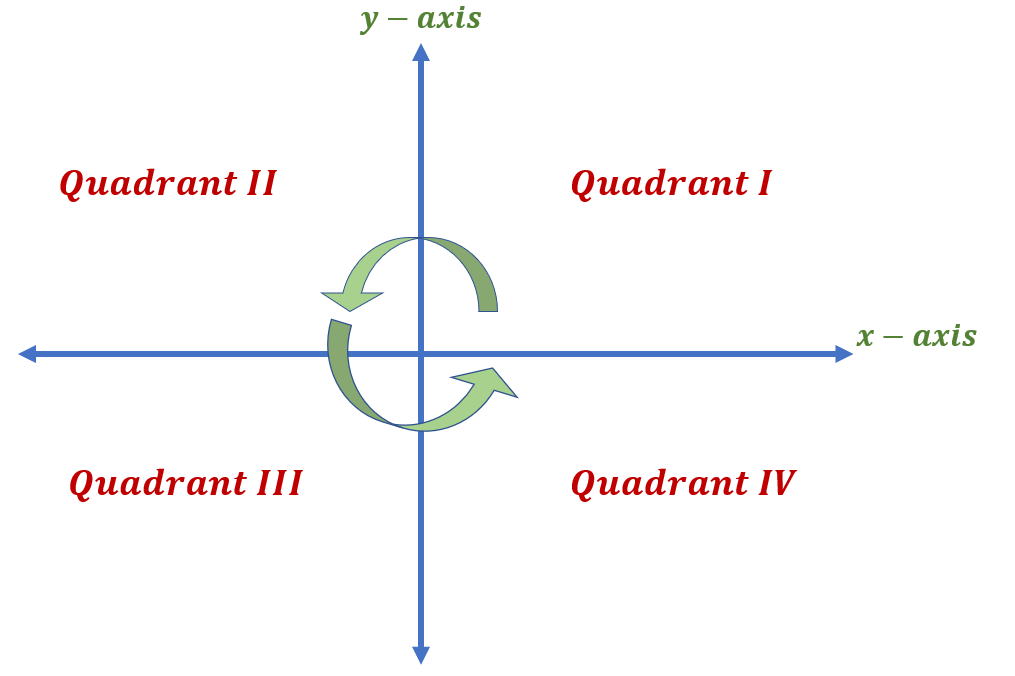
Quadrant I, or the first quadrant, is the upper right quadrant. Both the x – axis and y – axis have positive numbers in Quadrant I.
Quadrant II, or the second quadrant, is the upper left quadrant. In Quadrant II, the x – axis has negative numbers while the y – axis has positive numbers.
Quadrant III, or the third quadrant, is the bottom left quadrant. Both the x – axis and y – axis have negative numbers in Quadrant III.
Quadrant IV, or the fourth quadrant, is the bottom right quadrant. In Quadrant IV, the x – axis has positive numbers while the y – axis has negative numbers.
Recommended Worksheets
Number Lines and Coordinate Planes 6th Grade Math Worksheets
Cartesian Coordinate Plane (Adventure Themed) Worksheets
Graphing Points on the Coordinate Plane 5th Grade Math Worksheets









