What is Multiplication?
The process of finding out the product between two or more numbers is called multiplication. The result thus obtained is called the product. Suppose, you bought 6 pens on one day and 6 pens on the next day. Total pens you bought are now 2 times 6 or 6 + 6 = 12.
This can also be written as 2 x 6 = 12
Not the symbol used for multiplication. The symbol (x) is generally used to represent multiplication. Other common symbols that are used for multiplication are the asterisk (*) and dot (.)
Important terms in the multiplication
Some important terms used in multiplication are:
Multiplicand – The number to be multiplied is called the multiplicand.
Multiplier – The number with which we multiply is called the multiplier.
Product – The result obtained after multiplying the multiplier and the multiplicand is called the product.
The relation between the multiplier, multiplicand and the product can be expressed as:
Multiplier × Multiplicand = Product
Let us understand this using an example.
Suppose we have two numbers 9 and 5. We wish to multiply 9 by 5.
So, we express it as 9 x 5 which gives us 45.
Therefore, 9 x 5 = 45
Here, 9 is the multiplicand, 5 is the multiplier and 45 is the product.
Methods of multiplication
There are two methods of multiplying the numbers, namely the expanded notation method and the column method.
Expanded Notation Method
In the expanded notation method we expand the multiplicand as per the place values and then multiply each number by the multiplier. We then sum up all the results obtained to get our final answer. Let us understand it through an example.
For example, Multiply 1235 by 4
Solution
We will solve this step by step.
Step 1 – Write the number (multiplicand) in the expanded form. We get,
1235 = 1000 + 200 + 30 + 5
Step 2 – Multiply each number by the given number (multiplier) one by one. We get,
1000 x 4 + 200 x 4 + 30 x 4 + 5 x 4
= 4000 + 800 + 120 + 20
Step 3 – Add the results obtained. We get,
4000 + 800 + 120 + 20 = 4940 which is our final result
Hence, 1235 x 4 = 4940
This method, though simple, may not be suited for larger numbers. But it is used to understand the basic concepts of multiplication.
Column Method
In this method, we split the numbers into columns and multiply the numbers by the multiplicand one by one. There are two scenarios when using this method.
Let us understand them one by one
Multiplication without Regrouping
This method comes into force when we have smaller numbers that do not involve carrying forward any numbers to the digit at the next place value. Let us understand it through an example.
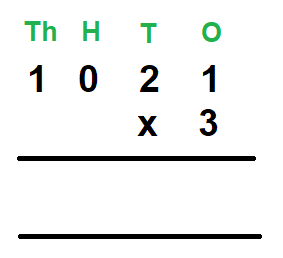
For example, Multiply 1021 by 3
Solution
We will use the following steps to obtain our result.
Step 1 – First we write the multiplicand and the multiplier in columns.
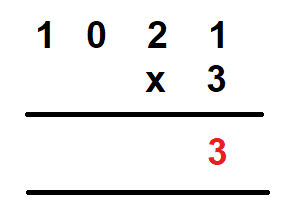
Step 2 – Now, we multiply the number at the one’s place by 3. We get
Step 3 – Now, we multiply the number at the ten’s place by 3. We get
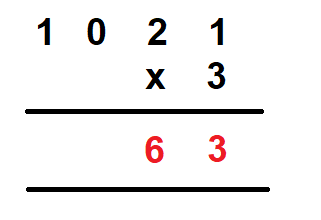
Step 4 – Next, we multiply the number at the hundred’s place by 3. We get
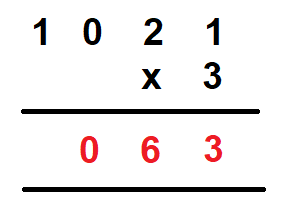
Step 5 – Last, we multiply the number at the thousand’s place by 3. We get
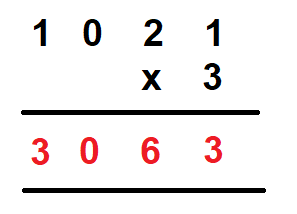
Therefore, 1021 x 3 = 3063
Multiplication with Regrouping
In the above case, we have small multiplications that did not involve two-digit results at any step. But in the case of larger numbers, there will be a need to carry forward the number to the number at the next place value. This is called Multiplication with Regrouping. Let us understand it through an example.
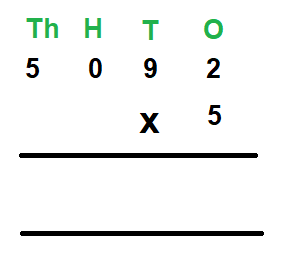
For example, Multiply 5092 by 5
Solution
We will use the following steps to obtain our result.
Step 1 – First we write the multiplicand and the multiplier in columns.
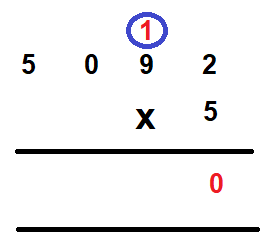
Step 2 – Multiply the one’s digit by 5. We have 2 x 5 = 10. Write 0 in the one’s column and carry over 1 to the ten’s column.
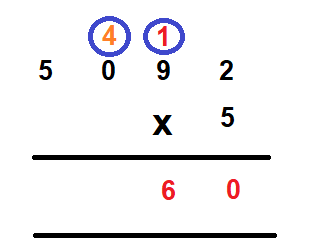
Step 3 – Multiply ten’s digit by 5. We get 9 x 5 = 45. Add 1 that was carried over to it to get 45 + 1 = 46. Now, write 6 in the ten’s column and carry over 4 to the hundred’s column.
Step 4 – Multiply the hundred’s digit by 5. We get 0 x 5 = 5. Now add 4 that was carried over to it and we get 4. Write 4 in the hundred’s column.
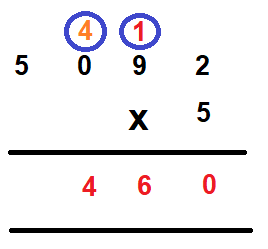
Step 5 – Multiply 5 with thousand’s digit. We get 5 x = 25. Write 5 in the thousand’s column and 2 in the ten thousand’s columns.
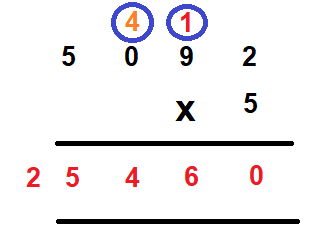
Hence, the final product is 25460.
Long Multiplication
Long multiplication is similar to the column method except for the fact that here we multiply the larger numbers. This method is used when the multiplicand is greater than 9, i.e. the multiplicand is more than a one-digit number. This method involves the following steps –
- First, we write the multiplicand and the multiplier in columns.
- First, multiply the number at the one’s place of the multiplier with all the numbers of the multiplicand and write them horizontally.
- Make sure you write numbers from right to left and each number below the corresponding place value of the multiplicand.
- Now, move to the next line.
- Place a 0 at the one’s place of this line.
- Now, look for the digit at the ten’s place of the multiplier. Multiply the number at the ten’s place of the multiplier with all the numbers of the multiplicand and write them horizontally in the line where you had marked 0.
- Again move to the next line.
- Place a 0 at the one’s as well as ten’s place of this line.
- Now, look for the digit at the hundred’s place of the multiplier. Multiply the number at the hundred’s place of the multiplier with all the numbers of the multiplicand and write them horizontally in the line where you had marked the two zeros.
- Continue in this manner by adding an extra zero in each line until you have reached the end of the multiplier
- Add the numbers vertically according to their place values.
- The number so obtained is your result.
Let us understand this by an example
For example, Multiply 132 by 13
Solution
1. First, we write the multiplicand and the multiplier in columns.

2. First multiply the number at the one’s place of the multiplier with all the numbers of the multiplicand and write them horizontally.
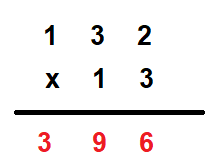
3. Place a 0 at the one’s place of the next line
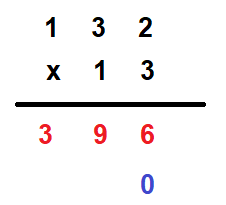
4. Now, look for the digit at the ten’s place of the multiplier. Multiply the number at the ten’s place of the multiplier with all the numbers of the multiplicand and write them horizontally in the line where you had marked 0.
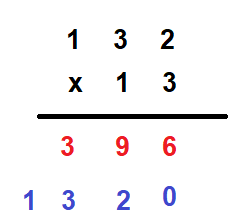
5. There is no more number in the multiplicand. Now, add the numbers vertically according to their place values.
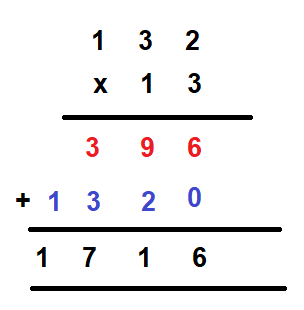
6. The final answer is 1716. Hence 132 x 13 = 1716
Let us see another example where we 3 digits in the multiplicand.
For example, Multiply 364 by 123
Solution
1. First we write the multiplicand and the multiplier in columns
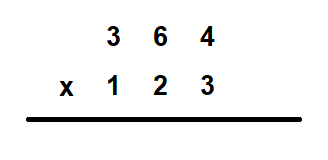
2. First multiply the number at the one’s place of the multiplier with all the numbers of the multiplicand and write them horizontally.
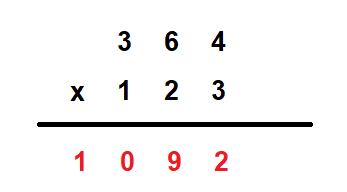
3. Place a 0 at the one’s place of the next line

4. Now, look for the digit at the ten’s place of the multiplier. Multiply the number at the ten’s place of the multiplier with all the numbers of the multiplicand and write them horizontally in the line where you had marked 0.
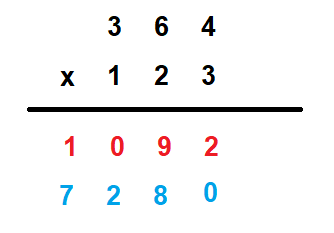
5. Place a 0 at the one’s as well as ten’s place of the next line.

6. Now, look for the digit at the hundred’s place of the multiplier. Multiply the number at the hundred’s place of the multiplier with all the numbers of the multiplicand and write them horizontally in the line where you had marked the two zeros.

7. There is no more number in the multiplicand. Now, add the numbers vertically according to their place values.
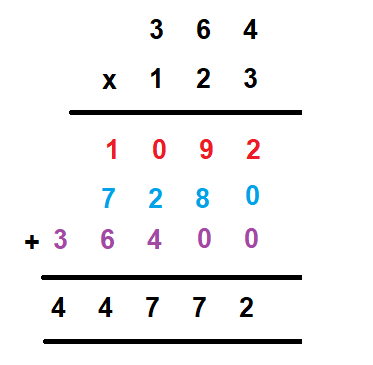
8. Hence the final product is 44,772. We can say that 364 x 123 = 44772
Multiplication by 10, 100 and 1000
- To multiply a number by 10, put 0 to the right of the number. For example, 435 x 10 = 4350
- To multiply a number by 100, put two zeros to the right of the number. For example, 435 x 100 = 43500
- To multiply a number by 1000, put three zeros to the right of the number. For example, 435 x 1000 = 435000
- To multiply a number by the product of 10, 100 and 1000 with the counting numbers, multiply the numbers with the non-zero numbers and then add the number of zeros to the result. For example, multiply 45 by 200. To solve this, we will first multiply 45 by 200. We get 45 x 2 = 90. Now we add 2 zeros ( as 200 had 2 zeros) to the right of 90. We get 9000.
- Hence, 45 x 20 = 9000
Properties of Multiplication
Commutative Property
Commutative Property states that when an operation is performed on two numbers, the order in which the numbers are placed does not matter. This means that if one number is multiplied with the other, it does not matter which number is marked as the multiplier and which number is marked as the multiplicand. Does this hold true for multiplication? Let us find out.
Let us take two numbers 8 and 5.
We first mark 8 as the multiplier and 5 as the multiplicand.
We get, 8 x 5 = 40.
Now let us reverse the order, i.e. 5 becomes the multiplier and 8 becomes the multiplicand.
Now, we get, 5 x 8 = 40.
Both the processes give us the same answer.
Therefore, we can say that multiplication satisfies the communicative property. We get
a x b = b x a
Hence, multiplication is communicative.
Associative Property
Associative Property states that when an operation is performed on more than two numbers, the order in which the numbers are placed does not matter. In the case of multiplication, this means that if we want to multiply 3 numbers, two of them can be chosen first, one as a multiplier and the second as a multiplicand. The result of the multiplication would serve as a multiplier and the third number as multiplicand to get the final answer. Is multiplication associative? Let us find out.
Let us take 3 numbers, 8, 5 and 2.
Let us take 8 and 5 first.
We first mark 8 as the multiplier and 5 as the multiplicand.
We get, 8 x 5 = 40.
Now, we multiply 40 by 2, we get 40 x 2 = 80
Now let us reverse the order and choose 5 and 2 first.
We get, 5 x 2 = 10
Now, we multiply this result by 8, we get, 10 x 8 = 80
Both the processes give us the same answer.
Therefore, we can say that multiplication satisfies the associative property. We get
(a x b) x c = a x (b x c)
Hence, multiplication is associative.
Multiplicative Property of “0”
The product of a number and 0 is always 0. For example,
45 x 0 = 0 x 45 = 0
Identity Property
A number is said to be an identity for multiplication, if, a number when multiplied by this identity number results in the number itself. Here, 1 is the identity element for multiplication. Let us see why?
4 x 1 = 4
15 x 1 = 15
20 x 1 = 20
Therefore, any number when multiplied by 1 number results in the number itself. This is the identity property of multiplication.
Multiplicative Inverse
A number is said to be multiplicative inverse if a number is multiplied by the multiplicative inverse, the result obtained is the identity of the operation, in this case, 1 ( 1 is the multiplicative identity of all numbers).
This means that for all non-zero numbers, the numbers when multiplied by their reciprocals will give the answer as 1, i.e.
4 x 1/4 = 1
Hence 1/a which is also written as a-1 is the multiplicative inverse of a.
Distributive Property of Multiplication over Addition / Subtraction
When two numbers are added or subtracted and the result is multiplied by another number, they can be multiplied separately.
Therefore, for any three numbers, a, b and c, distributive property of multiplication over addition states that
a x ( b + c) = (a x b) + (a x c)
Similarly, for any three numbers, a, b and c, the distributive property of multiplication over subtraction states that
a x ( b – c) = (a x b) – (a x c)
For example, let us first consider 10 x (18 + 12)
There are two ways to solve this.
First Method
First, we add 18 and 12, we get 30. Now we multiply, 30 and 10, we get 10 x 30 = 300
Second Method
Now, we use the distributive property of multiplication over addition.
We have 10 x (18 + 12)
= (10 x 18) + (10 x 12)
= 180 + 120
= 300
By both methods, we get the same answer. Hence,
10 x (18 + 12) = (10 x 18) + (10 x 12)
Now, let us consider 10 x (18 – 12)
Again let us solve this by both methods.
First method
We find out the difference between 18 and 12. We have 18 – 12 = 6
Now, we multiply 10 and 6. We get 10 x 6 = 60.
Second Method
Now, we use the distributive property of multiplication over subtraction.
We have 10 x (18 – 12)
= (10 x 18) – (10 x 12)
= 180 – 120
= 60
By both methods, we get the same answer. Hence,
10 x (18 – 12) = (10 x 18) – (10 x 12)
Multiplication in Real Life
We use multiplication in solving our day to day problems. Let us see some of the examples.
Example 1: There are 287 rows in a stadium. How many students can be seated in this stadium if each row has 165 seats to be occupied?
Solution
We are given that,
Number of rows in a stadium = 287
Number of seats in each row = 165
Total number of students that can be seated in the stadium = 287 x 165 = 47335.
Example 2: Henry bought 15 packets of cookies. Each packet contains 35 cookies. How many cookies in all does Henry have?
Solution
We are given that
Number of packets of cookies bought by Henry = 15
Number of cookies in each packet = 35
Total number of cookies that Henry has = 15 x 35 = 525
Recommended Worksheets
Multiplication and Division Problem Solving (Halloween Themed) Math Worksheets
Multiplication of Rational Algebraic Expressions with the Same Denominators (Pharmacy Themed) Worksheets
Multiplication of Integers with Unlike Signs (Banking and Finance Themed) Worksheets









