What is an inequality?
Inequality is a term derived from the word unequal. This means that inequality between two equations or expressions refers to the condition when they are not equal to each other. Inequality, can therefore be defined as – A statement involving variable ( s ) and the sign of inequality i.e. < , > , ≥, or ≤ is called an inequation or an inequality. In other words, If two real numbers or the algebraic expressions are related by the symbols “>”, “<”, “≥”, “≤”, then the relation is called an inequality.
An inequality may contain one or more variables. Also, it may be linear or quadratic or cubic inequation or an inequality.
Let us consider some examples that are inequalities –
- 3 x – 2 < 0
- 2 x + 3 > 0
- 5 x – 3 > 0
- 4x – 6y < 1
- 2 x + 5 y ≥ 0
- 2 x 2 + 3 x + 4 < 0
- x 2 + 3 x + 2 ≥ 5
- x 3 – 6 x 2 + 5 x – 8 < 0
- x 3 + 9 x 2 – 7 x – 9 ≤ 0
- – 2 x 2 + 9 x + 5 < 0
Linear inequalities in one variable
Let “ a “ be a non – zero real number and x be a variable. Then inequalities of the form a x + b < 0, a x + b > 0, a x + b ≤ 0 and a x + b ≥ 0 are known as linear inequalities in one variable x.
Let us understand it through some examples.
9 x + 5 < 0, 5 x – 7 > 0, – 5 x + 9 ≤ 0 and – 2 x + 7 ≥ 0 are known as linear inequalities in one variable x.
Linear inequalities in two variables
Let “ a “ and “ b “ be a non – zero real numbers and x and y be variables. Then inequalities of the form a x + b y < c, a x + b y > c, a x + b y ≤ c and a x + b y ≥ c are known as linear inequalities in two variables x and y.
Let us understand it through some examples.
9 x + 5 y < 7, 5 x – 7 y > – 4, – 5 x + 9 y ≤ 1 and – 2 x + 7 y ≥ – 8 are known as linear inequalities in two variables x and y.
Quadratic inequalities
Let “ a “ be an non –zero real number. Then an inequality of the form a x 2 + b x + c < 0, a x 2 + b x + c > 0, a x 2 + b x + c ≤ 0 and a x 2 + b x + c ≥ 0 are known as quadratic inequalities.
Inequality symbols
The symbols of “ not equal to ( ≠ ) “ is the most common symbol of an inequality. This can further be divided into two categories –
- Strict inequality
- Slack inequality
Let us understand them one by one.
Strict Inequality
The less than symbol ( < ) and the greater than symbol ( > ) are the two symbols that represent strict inequality. These symbols mean that a number is strictly less than or greater than another number. Let us understand this by some examples.
We know that 2 < 5 . This means that the number 2 is strictly less than the number 5. Similarly, 9 > 3 means that the number 9 is strictly greater than the number 3.
Slack Inequality
The less than or equal to symbol ( ≤ ) and the greater than or equal to symbol ( ≥ ) are the two symbols that represent slack inequality. These symbols mean that a number is less than or equal to or greater than or equal to another number. Let us understand this by an example.
2 x ≥ 17 means that the value of the variable x is such that 2 x is always greater than or equal to 17.
3 x ≤ – 8 means that the value of the variable x is such that 3 x is always less than or equal to 17.
Solving Inequalities
Solving an inequality is similar to solving any other linear equation. However, there are some rules that need to be kept in mind while solving these inequalities. These rules are –
- Same number may be added to ( or subtracted from ) both sides of an inequality without changing the sign of an inequality.
- Both sides of an inequality can be multiplied ( or divided ) by the same positive real number without changing the sign of an inequality. However, the sign of inequality is reversed when both sides of an inequality are multiplied or divided by a negative number.
- Any term of an inequality may be taken to the other side with its sign changed without affecting the sign of inequality.
Algorithm for solving an inequality
The following steps need to be followed when solving a linear inequality –
- Obtain the linear inequality
- Collect all terms involving the variable on one side of the inequality and the constant terms on the other side.
- Simplify both sides of the inequality in their simplest forms to reduce the inequality in the form a x < b or a x > b or a x ≥ b or a x ≤ b.
- Solve the inequality obtained in the previous step by dividing both sides of the inequality by the coefficient of the variable.
- Write the solution set obtained in the previous step in the form of an interval on the real line.
Let us understand it by an example.
Example
Solve the following inequality
2 x – 4 ≤ 0
Solution
We have been given the inequality 2 x – 4 ≤ 0. Let us use the steps defined above to solve this inequality. We will have
2 x – 4 ≤ 0
⇒ (2 x – 4 ) + 4 ≤ 0 + 4
⇒ 2 x ≤ 4
⇒ x ≤ 2
Hence, any real number less than or equal to 2 is a solution of the given inequality.
Graphing Linear Inequalities
We know how to graph a linear equation. But, how do we plot a linear inequality. Let us find out.
Let us consider the inequality x ≤ 2. The graph of this inequality will be –
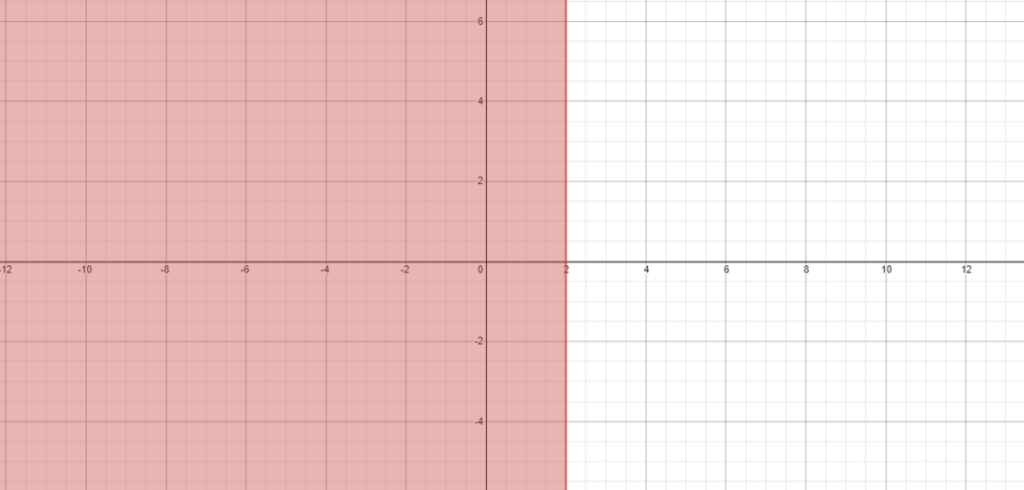
The shaded region represents the inequality x ≤ 2. The same graph can also be presented on a number line. the following will be the representation of x ≤ 2 on a number line.
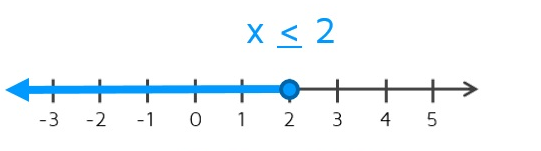
Let us consider some more examples.
Example
Plot the inequality x > 4 on a number line
Solution
The following will be the graphical representation of the inequality x > 4 on a number line –

Example
Plot the inequality x < 7 on a number line
Solution
The following will be the graphical representation of the inequality x < 7 on a number line –

Notice the open circles at one end. What do these signify? They represent the intervals of the inequality. Let us learn more about them.
An interval is a range of numbers between two given numbers and includes all of the real numbers between those two numbers.
Intervals and Inequalities
Intervals can be written using inequalities as well. Let us recall that math inequalities are the symbols that stand for less than, less than or equal to, greater than, and greater than or equal to. So we have
< symbol for less than
> symbol for greater than
≥ symbol for greater than or equal to
≤ symbol for less than or equal to
A helpful way to remember what each symbol means is to look at the size of each side. As shown below, the value that is on the larger side is greater and the value on the smaller side is less.
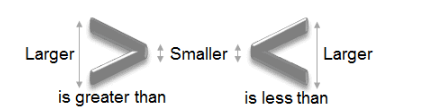
How can the above symbols be used to represent inequalities as intervals? Let us find out.
Closed Interval
As the name suggests, a closed interval is a closed group where the end points are included in the interval. Therefore, if we consider the above example, it would be a closed interval if we consider its end points as 0 and 9. So, we can say that, the interval X = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 } or X = { 0, 1 …………, 9 }. How do you represent it mathematically? Let us find out
Notation of a Closed Interval
The values in a closed interval are presented between square brackets, [ ]. This means that a square bracket is used to represent an interval when both the endpoints are included in the set. For instance, in the above example where we have an interval X that contains, whole numbers less than 10, we can represent it as –
X = [0, 9]
The expansion of this interval will be X = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 }
Now, let us see how to represent a closed interval on a number line.
Representation of a Closed Interval on a Number Line
We know how to represent numbers on a number line. How, do we represent the interval of a specific group of numbers?
Let us again consider the same example, where we have X = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 } and plot this interval on the number line. We will get,

Note the closed circles at the end points of the interval. This means that the said values are included in the interval and hence is a closed interval.
Open Interval
As the name suggests, a closed interval is an open group where the end points are not included in the interval. Therefore, if we consider the above example, it would be an open interval if we consider its end points as -1 and 10. How do you represent it mathematically? Let us find out
Notation of an Open Interval
The values in a closed interval are presented between square brackets, ( ). This means that a round bracket is used to represent an interval when both the endpoints are not included in the set. For instance, in the above example where we have an interval X that contains, whole numbers less than 10, we can represent it as –
X = ( -1, 10 ), where x W
The above representation means that X includes all numbers between -1 and 10 but not including these two end points.
The expansion of this interval will still be X = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 }
Now, let us see how to represent an open interval on a number line.
Representation of an Open Interval on a Number Line
Let us again consider the same example, where we have X = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 } and plot this as an open interval on the number line. We will get,

Note, the open circles at the end points -1 and 10. This represents that -1 and 10 are excluded from the interval but all numbers between -1 and 10 are included. Now, since the there is no whole number between -1 and 0 and between 9 and 10, the first and the last numbers to be included will be 0 and 10. So the end points -1 and 10 have been shown on the number line but in an open circle form indicating their exclusion from the interval. Therefore, this is how we represent an open interval on the number line.
Following steps should be considered while plotting an inequality on a number line or determining its interval –
- Determine the interval notation after graphing the solution set on a number line.
- The numbers in interval notation should be written in the same order as they appear on the number line, with smaller numbers in the set appearing first.
- If there is any inclusive inequality, which means that one of the end points is included in the interval, you denote with a square bracket.
- If there is any non-inclusive inequality, which means that one of the end points is not included in the interval, you denote with a round bracket.
- The symbol ( ) is read as infinity and indicates that the set is unbounded to the right on a number line. Interval notation requires a parenthesis to enclose infinity.
- Infinity is an upper bound to the real numbers but is not itself a real number: it cannot be included in the solution set.
Key Facts and Summary
- A statement involving variable ( s ) and the sign of inequality i.e. < , > , ≥, or ≤ is called an inequation or an inequality. In other words, If two real numbers or the algebraic expressions are related by the symbols “>”, “<”, “≥”, “≤”, then the relation is called an inequality.
- Let “ a “ be a non – zero real number and x be a variable. Then inequalities of the form a x + b < 0, a x + b > 0, a x + b ≤ 0 and a ≥ x + b 0 are known as linear inequalities in one variable x.
- Let “ a “ and “ b “ be a non – zero real numbers and x and y be variables. Then inequalities of the form a x + b y < c, a x + b y > c, a x + b y ≤ c and a x + b y ≥ c are known as linear inequalities in two variables x and y.
- Let “ a “ be an non –zero real number. Then an inequality of the form a x 2 + b x + c < 0, a x 2 + b x + c > 0, a x 2 + b x + c ≤ 0 and a x 2 + b x + c ≥ 0 are known as quadratic inequalities.
- The symbols of “ not equal to ( ) “ is the most common symbol of an inequality. This can further be divided into two categories – Strict inequality and Slack inequality.
- The less than symbol ( < ) and the greater than symbol ( > ) are the two symbols that represent strict inequality. These symbols mean that a number is strictly less than or greater than another number.
- The less than or equal to symbol ( ≤ ) and the greater than or equal to symbol ( ≥ ) are the two symbols that represent slack inequality. These symbols mean that a number is less than or equal to or greater than or equal to another number.
- Same number may be added to ( or subtracted from ) both sides of an inequality without changing the sign of an inequality.
- Both sides of an inequality can be multiplied ( or divided ) by the same positive real number without changing the sign of an inequality. However, the sign of inequality is reversed when both sides of an inequality are multiplied or divided by a negative number.
- Any term of an inequality may be taken to the other side with its sign changed without affecting the sign of inequality.
- Intervals can be written using inequalities as well.
Recommended Worksheets
Graphing Linear Inequalities (Civil Rights Movement Themed) Math Worksheets
One-variable Inequalities (Time Themed) Worksheets
Solving Word Problems Involving Linear Equations and Linear Inequalities 7th Grade Math Worksheets









