Introduction

Every time working with numbers, mathematicians want to increase the number of properties that these numbers have.

First, people learned to count and use natural numbers for counting. Then people noticed that the set of natural numbers is not closed under the subtraction, and so arrived negative numbers, which together with natural numbers and zero formed the set of integers. But integers are not closed under the division, the quotient of two non-zero integers could be a fraction. By adding fractional numbers to the set of integers, mathematicians introduced rational numbers.

We know that for two give integers, m and n, their sum m + n, product m x n and the difference m – n are always integers. However, it may not always be possible for a given integer to exactly divide another integer. In other words, the result of the division of an integer by a non-zero integer may or may not be an integer. For example, when 9 is divided by 4, the result is not an integer. In fact, $\frac{9}{4}$ is a fraction. Thus we need to extend the system of integers so that it may also be possible to divide any given integer by any other given integer different from zero. That is where we get the concept of rational numbers. Let us learn what are rational numbers and their importance and uses in Mathematics.

What are Rational Numbers?

Let’s remind which numbers we knew so far.

The most common numbers we come across are natural numbers (numbers used in counting). Counting numbers 1, 2, 3, …,n-1, n, n+1, … form a set of natural numbers.

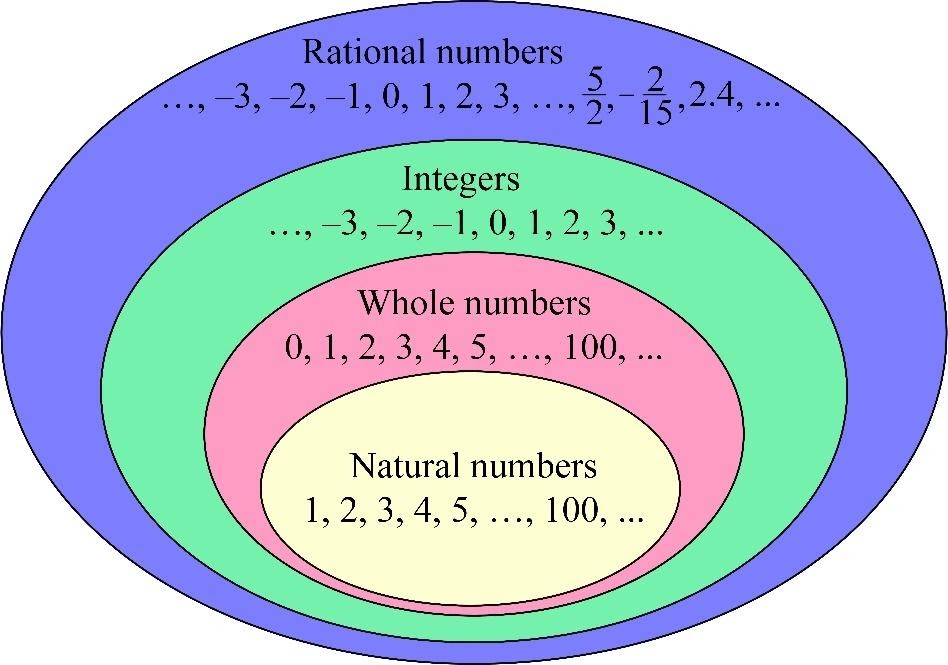
If we add 0 to the set of natural numbers, we get the set of whole numbers. So, all whole numbers are numbers of the form 0, 1, 2, 3, …, n-1, n, n+1, …

By adding opposite to natural numbers, we get the set of integer numbers or simply integers. All integers are numbers of the form …, -n, …, -2, -1, 0, 1, 2, …, n, … Notice that number 0 is the only number whose opposite is itself.

Extending the set of integers, we obtain a set of rational numbers. A rational number is a number that can be represented as a fraction pq of two integers such that denominator q≠0.

Rational numbers are A number of the form $\frac{p}{q}$ or a number that can be expressed in the form of $\frac{p}{q}$, where p and q are integers and q ≠ 0 is called a rational number.

In other words, a rational number is any number that can be expressed as the quotient of two integers with the condition that the divisor is not zero.

Examples of rational numbers include $-\frac{1}{7}, \,\frac{-5}{18}, \,\frac{11}{18}, \,\frac{-17}{9}$, etc.

In the rational number $\frac{p}{q}$, p is known as the numerator while q is known as the denominator.

Hence, if we can represent number as an arbitrary fraction with non-zero denominator, then this number is a rational number. For example,

Number	Number as a fraction	Rational?
15	$\frac{15}{1}$	Yes
-45	-$\frac{90}{2}$	Yes
0	$\frac{0}{7}$	Yes
√2	–	No
0.1111…	$\frac{1}{9}$	Yes
$\pi$	–	No

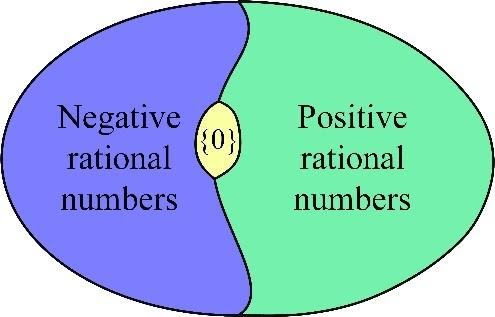
A rational number could be positive, zero or negative number.

If the numerator and denominator of a rational number are of the same sign (both positive or negative), then the rational number is positive.
If the numerator and denominator are of different signs, then the rational number is negative.
If the numerator is zero, the rational number is zero too. This number is neither positive, nor negative.

Positive Rational Number – A rational number is said to be positive if its numerator and denominator are either both positive integers or both are negative integers. For example, $\frac{5}{7}$ and $\frac{-5}{-7}$ are both positive rational numbers.

Negative Rational Number – A rational number is said to be negative if either its numerator or its denominator is a negative integer. For example, $\frac{-5}{7}$ and $\frac{5}{-7}$ are both negative rational numbers.

If the numerator and denominator of a rational number are multiplied or divided by a non-zero integer, we get a rational number which is equivalent to the given rational number. A rational number is said to be written in the standard form if the greatest common factor between numerator and denominator of the number is equal to 1. For example, rational number $\frac{1}{3}$ is written in the standard form, but equivalent to this number rational number $\frac{5}{15}$ is not written in the standard form.

Subsets of rational numbers

From what was said in the previous topic, we can conclude that set of integers is a subset of a set of rational numbers, a set of whole numbers is a subset of a set of integers, and a set of natural numbers is a subset of a set of whole numbers.

However, this is not the only way how we can interpret the set of rational numbers. We can consider that the set of rational numbers consists of three subsets: subset of positive rational numbers, subset of negative rational numbers and one-element subset zero.

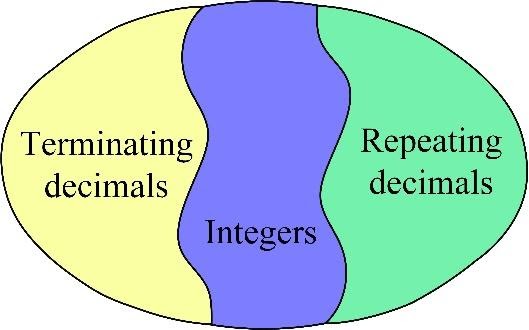
Or we can consider the set of rational numbers as the union of set of integers, set of repeating decimals and set of terminating decimals. Recall that a terminating decimal is a decimal that can be written as a fraction by using properties of place value (or simply decimal that has the end) and a repeating decimal is a decimal whose digits are periodic.

Properties of Rational Numbers

The properties of rational numbers are:

Every natural number is a rational number but a rational number may not be a natural number. This means that every natural number n can be written as $n=\frac{n}{1}$, such as we can write 5 as $\frac{5}{1}$, -9 as $\frac{-9}{1}$ and so on. However, every rational number cannot be written as a natural number such as $-\frac{-1}{7}, \,\frac{-5}{8}$ are rational numbers but they are not natural numbers.
Zero is a rational number. This is because 0 can be written in the form of $\frac{0}{1}$ which is a rational number.
Every integer is a rational number but a rational number need not be an integer. This is because every integer Z can be written in the form of $\frac{z}{q}$, such as $1=\frac{1}{1}\, -2=\frac{-2}{1}$, and so on. On the other hand, every rational number might not be an integer such as, $\frac{11}{18}, \,\frac{-17}{9}$, etc.
Every fraction is a rational number while every rational number is not a fraction. For example, $\frac{11}{-18}$ is a rational number while $\frac{11}{-18}$ is not a fraction as it has a negative sign in the denominator.
If $\frac{p}{q}$ is a rational number and m is an integer, then $\frac{p}{q}=\frac{p\times m}{q\times m}$
In other words, a rational number remains unchanged if we multiply its numerator and denominator by the same non-zero integer.
If $\frac{p}{q}$ is a rational number and m is an integer, then $\frac{p}{q}=\frac{p/m}{q/m}$ In other words, a rational number remains unchanged if we divide its numerator and denominator by the same non-zero integer.

PROPERTY 1: There is infinite number of rational numbers but all rational numbers can be counted.

Represent rational numbers as a rectangular table, where the row number is the numerator of the fraction, and the column number is the denominator of the fraction. There are infinite numbers of rows and columns as set of integers is infinite. So, there is infinite number of rational numbers.

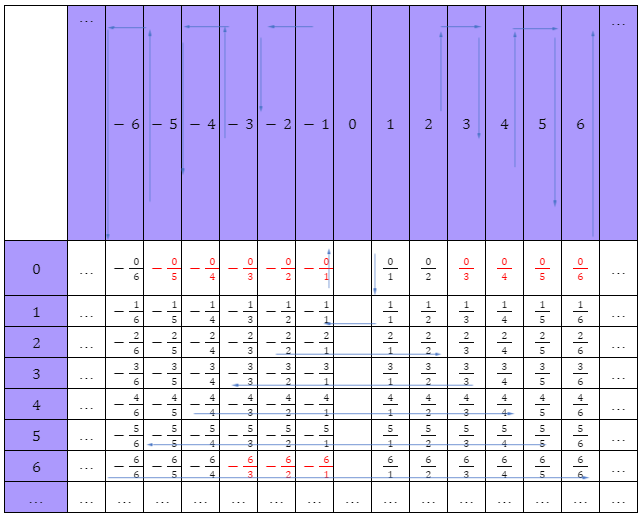
Move along the arrows and “number” the rational numbers:

$\frac{0}{1}$ is the 1^st number, $\frac{1}{1}$ is the 2^nd number, -$\frac{1}{1}$ is the 3^rd number, …,

discarding the equivalent fractions to those already numbered. In this way we can count all rational numbers.

A set, which elements can be “numbered” using natural numbers is called countable set. Therefore, the set of rational numbers is a countable set.

PROPERTY 2: There is always a rational number between any two rational numbers. Moreover, there is infinite number of rational numbers between any two rational numbers.

Let’s think a little about the first sentence. If we take two rational numbers of different signs, there will always be zero between them, so the statement is true. If we take two rational numbers of the same sign, for example two positive numbers, we can always find a rational number between them. Demonstrate this with some examples.

Take fractions with the same denominators $\frac{2}{7}$ and $\frac{4}{7}$, there is always a fraction $\frac{3}{7}$ between $\frac{2}{7}$ and $\frac{4}{7}$. But what if numerators of the fractions are consecutive integers?
Take fractions with the same denominators and consecutive numerators, $\frac{2}{7}$ and $\frac{3}{7}$. We can convert these two fractions to equivalent fractions, for example, with denominators 14. So, $\frac{2}{7}=\frac{2×2}{7×2}=\frac{4}{14}$ and $\frac{3}{7}=\frac{3×2}{7×2}=\frac{6}{14}$. Like in the first case, there is always fraction $\frac{5}{14}$ between $\frac{2}{7}$ and $\frac{3}{7}$. But what if denominators of the fractions are different?
Take arbitrary two fractions with different denominators, $\frac{2}{7}$ and $\frac{1}{6}$. We can convert these two fractions to equivalent fractions, for example, with denominators 6×7=42. So, $\frac{2}{7}=\frac{2×6}{7×6}=\frac{12}{42}$ and $\frac{1}{6}=\frac{1×7}{6×7}=\frac{7}{42}$. It is easy to see that there is at least one fraction between $\frac{7}{42}$ and $\frac{12}{42}$.

Using the algorithm illustrated in these examples, you can write a general rule for finding at least one fraction between two others. But what about infinite number of fractions between any two fractions? This can be explained very simply: if you increase the common denominator of two fractions each time, multiplying it by consecutive natural numbers, then more and more different numerators will be placed between the corresponding numerators each time.

Let us demonstrate it on fractions $\frac{2}{7}=\frac{12}{42}$ and $\frac{1}{6}=\frac{7}{42}$.

There are four different fractions between $\frac{1}{6}=\frac{7}{42}$ and $\frac{2}{7}=\frac{12}{42}$:

$\frac{7}{42},\: \frac{8}{42},\:\frac{9}{42},\:\frac{10}{42},\:\frac{11}{42},\:\frac{12}{42}$

Multiply the denominators by 2. There are nine different fractions between $\frac{1}{6}=\frac{14}{84}$ and $\frac{2}{7}=\frac{24}{84}$:

$\frac{14}{84},\: \frac{15}{84},\:\frac{16}{84},\:\frac{17}{84},\:\frac{18}{84},\:\frac{19}{84},\:\frac{20}{84},\:\frac{21}{84},\:\frac{22}{84},\:\frac{23}{84},\: \frac{24}{84}$

But four of them are equivalent to the fractions above, so there are five more additional different fractions between numbers $\frac{1}{6}$ and $\frac{2}{7}$. Multiply the denominators by 3. There are fourteen different fractions between $\frac{1}{6}=\frac{21}{126}$ and $\frac{2}{7}=\frac{36}{126}$:

$\frac{21}{126},\:\frac{22}{126},\:\frac{23}{126},\:\frac{24}{126},\:\frac{25}{126},\:\frac{26}{126},\:\frac{27}{126},\:\frac{28}{126},\:\frac{29}{126},\:\frac{30}{126},\:\frac{31}{126},\:\frac{32}{126},\:\frac{33}{126},\:\frac{34}{126},\:\frac{35}{126},\:\frac{36}{126}$

But four of them are equivalent to the fractions above, so, there are 10 more additional different fractions between numbers $\frac{1}{6}$ and $\frac{2}{7}$, 19 fractions in total.

Continuing in the same way, we get more and more fractions between two given rational numbers. This process will never end, because there is no largest possible denominator for two fractions.

CLOSURE PROPERTY: An operation is said to be closed on a set of rational numbers if the result of this operation belongs to the set of rational numbers.

If a and b are two rational numbers, then a*b is a rational number too.

Addition, subtraction and multiplication are closed operations on a set of rational numbers. Division of non-zero rational numbers is a closed operation on a set of non-zero rational numbers.

COMMUTATIVE PROPERTY: An operation is said to be commutative on a set of rational numbers if when we change the order of operation, the result remains unchanged.

If a and b are two rational numbers, then a*b=b*a.

Addition and multiplication are commutative operations.

Subtraction and division are not commutative operations. This can be seen from the following examples

$\frac{3}{2}-\frac{1}{2}=\frac{2}{2}=1$ but $\frac{1}{2}-\frac{3}{2}=-\frac{2}{2}=-1$

12÷6=2 but 6÷12=12

ASSOCIATIVE PROPERTY: An operation is said to be associative on a set of rational numbers if you can rearrange the parentheses without rearranging the numbers and the result remains the same.

If a, b and c are three rational numbers, then (a*b)*c=a*(b*c).

Addition and multiplication are associative operations.

Subtraction and division are not associative operations. This can be seen from the following examples

$\frac{5}{2}-(\frac{3}{2}-\frac{1}{2})=\frac{5}{2}-\frac{2}{2}=\frac{3}{2}$ but $(\frac{5}{2}-\frac{3}{2})-\frac{1}{2}=\frac{2}{2}-\frac{1}{2}=\frac{1}{2}$

(12÷6)÷2=2÷2=1 but 12÷(6÷2)=12÷3=4

DISTRIBUTIVE PROPERTY: when we multiply the sum (difference) of two or more rational numbers by a third number, then it will give same result as multiplying each number individually by the number and then adding (subtracting) each of the multiplication results.

If a, b and c are three rational numbers,

then a+b×c=a×c+b×c and a-b×c=a×c-b×c.

ADDITIVE IDENTITY: The set is said to have an additive identity if the sum of any number from the set and this additive identity is the number itself. Usually, we denote additive identity as 0.

If a is a rational number, then a+0=0+a=a.

MULTIPLICATIVE IDENTITY: The set is said to have a multiplicative identity if the product of any number from the set and this multiplicative identity is the number itself. Usually, we denote multiplicative identity as 1.

If a is a rational number, then a×1=1×a=a.

MULTIPLICATION BY ZERO: When a rational number is multiplied to 0, the result is always 0.

If a is a rational number, then a×0=0×a=0

INVERSE PROPERTY: A set has the inverse property under an arithmetic operation if every element of the set has an inverse element. An inverse of an element is another element in the set that, when combined on the right or the left through the operation, always gives the identity element as the result. An inverse under addition to element a usually is denoted as -a.

If a is a rational number, then a+-a=-a+a=0

An inverse under multiplication to element a usually is denoted as a-1.

If a is a non-zero rational number, then a×a^-1=a^-1×a=1

Actually, the inverse under the multiplication of non-zero rational number is its reciprocal.

DIVISION BY ZERO: Division of a rational number by 0 is not defined.

If x is a rational number then $\frac{x}{0}$ is not defined

Equivalent Rational Numbers

If $\frac{p}{q}$ is a rational number and m is a non-zero integer, then $\frac{p\times m}{q\times m}$ is a rational number equivalent to $\frac{p}{q}$.

For example, the equivalent of the rational number $\frac{3}{4}$ will be

$\frac{3\times 2}{4\times 2}=\frac{6}{8}, \,\frac{3\times 3}{4\times 3}=\frac{9}{12}$ and so on.

Standard Form of a Rational Number

We know that a number of the form $\frac{p}{q}$ or a number that can be expressed in the form of $\frac{p}{q}$, where p and q are integers and q ≠ 0 is called a rational number. So how do we define the standard form of a rational number?

Definition – A rational number $\frac{p}{q}$ is said to be in the standard form if q is positive and the integers p and q have no common divisor other than 1.

In order to express a given rational number in the standard form, the following steps should be followed:

Step 1 – Check whether the given number is in the form of $\frac{p}{q}$ . i.e. a rational number.

Step 2 – See whether the denominator of the rational number is positive or not. If it is negative, multiply or divide the numerator as well as the denominator by -1 so that the denominator becomes positive.

Step 3 – Find the greatest common divisor (GCD) of the absolute values of the numerator and the denominator.

Step 4 – Divide the numerator and the denominator of the given rational number by the GCD (HCF) obtained in step III. The rational number so obtained is the standard form of the given rational number.

Let us understand the above steps with the help of some examples.

Example 1: Express the following rational numbers in standard form

a) $\frac{-8}{28}$

b) $\frac{-12}{30}$

Solution

a) We have been given the rational number $\frac{-8}{28}$ and we need to express it in its standard form.

Let us find our answer using the above steps. We can see that the number is given to us in the form of $\frac{p}{q}$. Therefore, we can move to step 2.

The next step is to check whether the denominator of the rational number is positive or not. We can see that the number in the denominator is 28 which, is a positive number. In order to express it in standard form, we must divide its numerator and the denominator by the greatest common divisor of 8 and 28.

The greatest common divisor of 8 and 28 is 4.

Therefore,

Dividing the numerator and the denominator of $\frac{-8}{28}$ by 4, we get

$\frac{-8}{28}=\frac{-8/4}{28/4}=\frac{-2}{7}$

Hence, the standard form of $\frac{-8}{28}$ is $\frac{-2}{7}$

b) The number is given to us $\frac{-12}{-30}$

Again, we will find our answer using the above steps. We can see that the number is given to us in the form of $\frac{p}{q}$ . Therefore, we can move to step 2.

The next step is to check whether the denominator of the rational number is positive or not. We can see that the number in the denominator is -30 which, is a negative number.

Therefore, first, we will have to make the denominator positive. In order to do so, we will multiply the numerator as well as the denominator by -1.

Hence, multiplying the numerator and the denominator by -1 we get,

$\frac{p}{q}=\frac{(-12)\times (-1)}{(-30)\times(-1)}=\frac{12}{30}$

Now, we have a positive denominator; therefore let us move to the next step.

In order to express it in standard form, we must divide its numerator and the denominator by the greatest common divisor of 12 and 30.

The greatest common divisor of 12 and 30 is 6.

Therefore,

Dividing the numerator and the denominator of $\frac{12}{30}$ by 6, we get

$\frac{12}{30}=\frac{12/6}{30/6}=\frac{2}{5}$

Hence, the standard form of $\frac{-12}{-30}$ is $\frac{2}{5}$

Arithmetic Operations on Rational Numbers

If each rational number can be represented as a fraction, then arithmetic operations with rational numbers are arithmetic operations with fractions. Herewith, we remember that the result of an arithmetic operation is usually written as a fraction in a standard form.

Let us now learn how to perform different mathematical operations on two or more rational numbers.

Addition of Rational Numbers

The addition of rational numbers is carried out in the same way as that of fractions. If two rational numbers are to be added we first express each one of them as rational numbers with a positive denominator. For addition purposes, we divide the rational numbers into two categories, namely,

Rational Numbers with the same denominator
Rational Numbers with different denominator
Or we can use general rule of addition of fractions

Rational Numbers with the same denominator

Two rational numbers with the same denominators can be added by adding their numerators, keeping with the same denominator.

In order to add two rational numbers with the same denominator, we follow the following steps:

Obtain the numerators of the two given rational numbers and their common denominator
Add the numerators obtained in the first step.
Write a rational number whose numerator is the sum obtained in the second step and the denominator is the common denominator of the given rational numbers.

Let us understand this through an example.

Example 1:

Suppose we want to add the rational numbers $\frac{3}{5}$ and $\frac{13}{5}$

Solution

Here we can see that both the rational numbers have the same denominator, i.e. 5.

Therefore, we go by the above-defined steps.

We check the numerators of both the rational numbers. They are 3 and 13.

Then, we add these numerators and get 3 + 13 = 16.

Now, we write the sum of these rational numbers as $\frac{16}{5}$

Hence, $\frac{3}{5}+\frac{13}{5}=\frac{16}{5}$

Example 2:

$\frac{2}{7} + \frac{3}{7} = \frac{2+3}{7} = \frac{5}{7}$

Now, we have understood how to add two rational numbers having the same denominator. What if the denominators are different? Let us find out

Rational Numbers with different denominator

Two rational numbers with different denominators can be added by converting them to equivalent fractions with the same denominators and using the rule for rational numbers with the same denominators.

To find the sum of two rational numbers which do not have the same denominator, we will follow the following steps:

Obtain the rational numbers and see whether their denominators are positive or not. If the denominator of one ( or both ) of the numbers is negative, rewrite it so that the denominator becomes positive.
Obtain the denominators of the rational numbers in the first step.
Find the LCM of the denominator obtained in the previous step.
Express each one of the rational numbers in the first step so that the LCM obtained in step 2 becomes their common denominator.
Write a rational number whose numerator is equal to the sum of the numerators of the rational numbers obtained in the fourth step and denominators as the LCM obtained in the third step.
The rational number obtained in the fifth step is the required form.

Let us understand this through an example.

Example 1:

Suppose we want to add $\frac{5}{12}$ and $\frac{3}{8}$

Solution

We have been given two rational numbers $\frac{5}{12}$ and $\frac{3}{8}$

Here we can clearly see that the denominators of the given numbers are positive. Also, the denominators are different.

So, we take the LCM of the denominators i.e. LCM of 12 and 8.

We know that the LCM of the numbers 12 and 8 will be 24.

So, now we express $\frac{5}{12}$ and $\frac{3}{8}$ into the forms in which both of them have the same denominator 24. We get

$\frac{5}{12}=\frac{5\times 2}{12\times2}=\frac{10}{24}$

$\frac{3}{8}=\frac{3\times 3}{8\times3}=\frac{9}{24}$

Now, we can see that we have the denominators with the same denominator. So we add the numerators and get the rational numbers according to step 5. We now have,

$\frac{5}{12}+\frac{3}{8}=\frac{10}{24}+\frac{9}{24}=\frac{19}{24}$

Hence, $\frac{5}{12}+\frac{3}{8}=\frac{19}{24}$

Example 1:

$\frac{2}{9}+\frac{1}{6} = \frac{2×2}{9×2}+\frac{1×3}{6×3}=\frac{4}{18}+\frac{3}{18}=\frac{4+3}{18}=\frac{7}{18}$

General Rule of Addition of Fractions

We can use general rule of addition of fractions:

$\frac{a}{b}+\frac{c}{d}=\frac{ad+bc}{bd}$

Example:

$\frac{2}{9}+\frac{1}{6}=\frac{2×6+1×9}{9×6}=\frac{12+9}{54}=\frac{21}{54}=\frac{7×3}{18×3}=\frac{7}{18}$

Subtraction of Rational Numbers

If $\frac{a}{b}$ and $\frac{c}{d}$ are two rational numbers, then subtracting $\frac{c}{d}$ from $\frac{a}{b}$ means adding inverse (negative) of $\frac{c}{d}$ to $\frac{a}{b}$. The subtraction of $\frac{c}{d}$ from $\frac{a}{b}$ is written as $\frac{a}{b}-\frac{c}{d}$

Thus, we have

$\frac{a}{b}-\frac{c}{d}=\frac{a}{b}+(\frac{-c}{d})$ [because the additive inverse of $\frac{c}{d}$ is $\frac{-c}{d}$ ]

Let us understand this through an example.

Example

Subtract $\frac{3}{4}$ from $\frac{5}{6}$

Solution

The additive inverse of $\frac{3}{4}$ is $\frac{-3}{4}$

Therefore,

To find the value of $\frac{5}{6}-\frac{3}{4}$

We first make the denominators the same.

LCM of 6 and 4 is 12.

Therefore

$\frac{5}{6}=\frac{5\times 2}{6\times2}=\frac{10}{12}$ and

$\frac{3}{4}=\frac{3\times 3}{4\times3}=\frac{9}{12}$

Therefore,

$\frac{5}{6}-\frac{3}{4}=\frac{10}{12}-\frac{9}{12}=\frac{10-9}{12}=\frac{1}{12}$

Hence, $\frac{5}{6}-\frac{3}{4}=\frac{1}{12}$

Multiplication of Rational Numbers

Multiplication of rational numbers is similar to the multiplication of fractions. To obtain the product of two or more rational numbers, we multiply the numerators with the numerators and the denominator with the denominators. The following steps are involved in multiplying two or more rational numbers:

First, we need to multiply all the numerators.
Next, we need to multiply all the denominators
Lastly, we need to simplify the rational number, if required

Therefore, we can say that

Product of rational numbers = $\frac{Product\,of\,the\,Numerators}{Product\,of\,the\,denominators}$

Thus if $\frac{a}{b}$ and $\frac{c}{d}$ are two rational numbers then,

$\frac{a}{b}\times \frac{c}{d}=\frac{a\times c}{b\times d}$

Let us understand this through an example.

Example

Suppose we want to find the value of $\frac{3}{4}\times \frac{5}{7}$

Solution

We have to find the value of $\frac{3}{4}\times \frac{5}{7}$

According to the given formula for multiplication we have,

$\frac{3}{4}\times \frac{5}{7}=\frac{3\times 5}{4\times 7}=\frac{15}{28}$

Hence, $\frac{3}{4}\times \frac{5}{7}=\frac{15}{28}$

Reciprocal of a Non-zero Rational Number

What do we mean by reciprocal of a rational number? Let us find out.

For every, non-zero rational number $\frac{a}{b}$, there exists a rational number $\frac{b}{a}$ such that

$\frac{a}{b}\times\frac{b}{a}=1$

The rational number $\frac{b}{a}$ is called the multiplicative inverse or reciprocal of $\frac{a}{b}$ and is denoted by $(\frac{a}{b})^{-1}$

Division of Rational Numbers

If $\frac{a}{b}$ and $\frac{c}{d}$ are two rational numbers such that $\frac{c}{d}\neq 0$ then the result of dividing $\frac{a}{b}$ by $\frac{c}{d}$ is the rational number obtained on multiplying $\frac{a}{b}$ by the reciprocal of $\frac{c}{d}$.

$\frac{a}{b} / \frac{c}{d}=\frac{a}{b}\times\frac{d}{c}$

Let us understand it through an example

Example

Suppose we want to find the value of $\frac{3}{5} / \frac{4}{25}$

First, we will find the reciprocal of $\frac{4}{25}$ which is $\frac{24}{4}$

Therefore, $\frac{3}{5} / \frac{4}{25}=\frac{3}{5}\times\frac{25}{4}=\frac{15}{4}$

Hence, $\frac{3}{5} / \frac{4}{25}=\frac{15}{4}$

Rational numbers on the number line

We already know how integers are located on a number line.

Let’s look at specific examples how positive and negative proper and improper fractions can be located on a number line.

1) Positive proper fraction $\frac{3}{4}$.

Since each positive proper fraction is between 0 and 1, divide the unit interval (0, 1) into four congruent parts, count three such parts from zero to the right and place a mark that defines $\frac{3}{4}$.

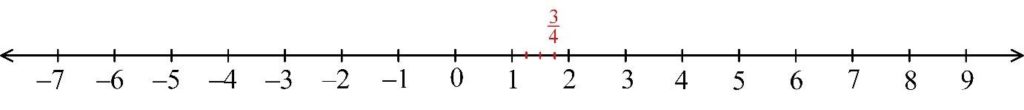
2) Negative proper fraction -$\frac{3}{4}$.

Complete the same steps for the interval (-1, 0), count three identical parts to the left and mark -$\frac{3}{4}$.

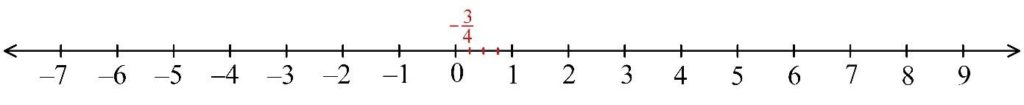
3) Positive improper fraction $\frac{13}{2}$.

First, convert the given rational fraction into mixed number to find between which two whole numbers the fraction lies on the number line.

$\frac{13}{2}=\frac{2×6+1}{2}=6+\frac{1}{2}=6\frac{1}{2}$

Mixed number 6$\frac{1}{2}$ is between 6 and 7 at $\frac{1}{2}$ of the interval.

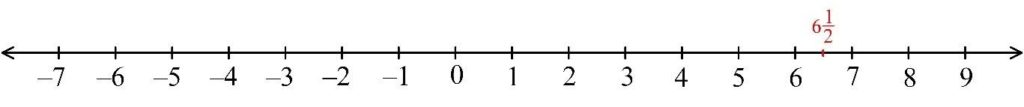
4) Negative improper fraction -$\frac{13}{2}$.

Complete the same steps for the interval (-7, -6), and mark -6$\frac{1}{2}$ at $\frac{1}{2}$ to the left of -6.

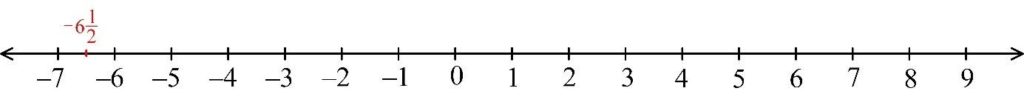
Rational numbers vs irrational numbers

All the numbers that are non-rational numbers are irrational numbers. A set of rational numbers and a set of irrational numbers together form a set of real numbers.

All rational numbers can be represented as fractions. Unlike rational numbers, which can be represented as fractions, irrational numbers cannot be represented as fractions. If an irrational number is represented as a decimal, it can never be a terminating or repeating decimal. The irrational number that most often occurs in mathematics can be written down as decimal 3.1415926535… This decimal is neither terminating nor repeating.

Rational number	Irrational number
Can be represented as a fraction	Cannot be represented as a fraction
Can be terminating decimals	Cannot be terminating decimals
Can be repeating decimals	Cannot be repeating decimals
Contains natural numbers, whole numbers and integers	Does not contain any of the other sets of numbers
Square roots of perfect square numbers are rational	Square roots of non-perfect square numbers are irrational

Quiz

In each statement, change one word to get the correct statement.
- Each rational number cannot be represented as a repeating decimal.
- Subtraction of rational numbers is a commutative operation.
- Each rational number is the ratio of two non-zero whole numbers.

SOLUTION: a) Actually, each rational number can be represented as a repeating decimal. So, replacing cannot with can or rational with irrational, the statement a) becomes true.

b) Subtraction of rational numbers is not commutative. There are two commutative operations on the set of rational numbers: addition and multiplication. So, change subtraction with addition or multiplication.

c) The ratio of two non-zero whole numbers is always a positive number, it rejects all negative rational numbers. Therefore, in this case you need to change the word whole with the word integer.

ANSWER: a) cannot with can or rational with irrational b) subtraction with addition or multiplication c) whole with integer

Which statement is true?
- Between any two rational numbers there is always an integer.
- Between any two integers there is always infinite number of rational numbers.
- The set of integers contains the set of rational numbers.
- 0 is irrational number.

SOLUTION: a) This statement is false. Between rational numbers 0.5 and 0.6 there are no integers.

b) This statement is true; it is essentially a property 2.

c) This statement is false. The set of rational numbers contains the set of integers but not vice versa.

d) This statement is false, zero is rational number, it can be represented as a fraction with zero numerator and an arbitrary non-zero denominator.

ANSWER: a) False b) True c) False d) False

Identify which number is rational and which is not.

$-1.76,\:\sqrt[3]{4},\:1.939393…,\:\sqrt{2500},\:\frac{30}{4},\:2^{-3},\:3+\pi$

SOLUTION: Number -1.76 has the end, so it is a terminating decimal and is a rational number.

It is impossible to get the cube root of a number 4, so $\sqrt[3]{4}$ is an irrational number.

Number 1.939393… is a repeating decimal, it can be represented as $\frac{31}{33}$, so it is a rational number.

Number $\sqrt{2500}$ is an integer as $\sqrt{2500}$=50, s it is a rational number too.

Number $\frac{30}{4}$ is a rational number by definition.

Number 2^-3 can be rewritten as $\frac{1}{2^3}=\frac{1}{8}$ and is a rational number by definition too.

Number is an irrational number, therefore, number 3+π is an irrational number too.

ANSWER: Rational numbers: $-1.76,\: 0.939393…,\: \sqrt{2500},\: \frac{30}{4}, 2^{-3};\: Irrational\: numbers:\: \sqrt[3]{4}, 3+\pi$

Find at least 7 different rational numbers between $\frac{1}{2}$ and $\frac{2}{3}$.

SOLUTION: First, rewrite fractions $\frac{1}{2}$ and $\frac{2}{3}$ with 6 in denominator:

$\frac{1}{2}=\frac{1×3}{2×3}=\frac{3}{6}$ and $\frac{2}{3}=\frac{2×2}{3×2}=\frac{4}{6}$

There are no fractions with denominator of 6 between these two fractions. Take quite large multiple of 6, for example 60. Then

$\frac{1}{2}=\frac{1×30}{2×30}=\frac{30}{60}$ and $\frac{2}{3}=\frac{2×20}{3×20}=\frac{40}{60}$

Fractions $\frac{31}{60},\:\frac{32}{60},\:\frac{33}{60},\:\frac{34}{60},\:\frac{35}{60},\:\frac{36}{60},\:\frac{37}{60},\:\frac{38}{60},\:\frac{39}{60}$ lie between fractions $\frac{30}{60}=\frac{1}{2}$ and $\frac{40}{60}=\frac{2}{3}$.

It was possible to take a smaller or even a larger denominator, and get at least seven different rational numbers between given fractions. Therefore, the solution to this problem is not the only one.

POSSIBLE ANSWER: $\frac{31}{60},\:\frac{32}{60},\:\frac{33}{60},\:\frac{34}{60},\:\frac{35}{60},\:\frac{36}{60},\:\frac{37}{60},\:\frac{38}{60},\:\frac{39}{60}$

Come up with two irrational numbers a and b for which:
- a+b is a rational number;
- a-b is a rational number;
- a×b is a rational number;
- a÷b is a rational number.

SOLUTION: a) a=√2, b=-√2, then

a+b=√2+(-√2)=0

b) a= b=√2, then

a-b=√2-√2=0

c) a= b=√2, then

axb=√2x√2=2

d) a= b=√2, then

a÷b=√2÷√2=1
ANSWER: b) and d)

Solved Examples

Example 1

The product of two rational numbers is $\frac{-28}{81}$. If one of the numbers is $\frac{14}{27}$, find the other.

Solution

We have been given that the product of two rational numbers is $$ and one of the numbers is $$.

Let the other number be “p”. Therefore, we will have

$p\times\frac{14}{27}=\frac{-28}{81}$

$p=\frac{-28}{81} /\frac{14}{27}$

$p=\frac{-28}{81}\times\frac{27}{14}=\frac{-2}{3}$

Hence, the other number is $\frac{-2}{3}$

Example 2

The sum of two rational numbers is $\frac{-3}{5}$. If one of the numbers is $\frac{-9}{20}$, find the other.

Solution

We have been given that the sum of two rational numbers is $\frac{-3}{5}$ and one of the numbers is $\frac{-9}{20}$.

Let the other number be “p”.

Therefore,

$p+\frac{-9}{20}=\frac{-3}{5}$

⇒ $p=\frac{-3}{5}-(\frac{-9}{20})$

⇒ $p=\frac{-3}{5}+\frac{9}{20}$

⇒ $p=\frac{(-3)\times4+(9\times1)}{20}$

⇒ $p=\frac{(-12)+9}{20}$

⇒ $p=\frac{-3}{20}$

Hence, the other number is $\frac{-3}{20}$

Remember

A number of the form $\frac{p}{q}$ or a number that can be expressed in the form of $\frac{p}{q}$, where p and q are integers and q ≠ 0 is called a rational number.
If $\frac{p}{q}$ is a rational number and m is a non-zero integer, then $\frac{p\times m}{q\times n}$ is a rational number equivalent to $\frac{p}{q}$.
A rational number $\frac{p}{q}$ is said to be in the standard form if q is positive and the integers p and q have no common divisor other than 1.
The addition of rational numbers is carried out in the same way as that of fractions.
If $\frac{a}{b}$ and $\frac{c}{d}$ are two rational numbers, then subtracting $\frac{c}{d}$ from $\frac{a}{b}$ means adding inverse ( negative ) of $\frac{c}{d}$ to $\frac{a}{b}$. The subtraction of $\frac{c}{d}$ from $\frac{a}{b}$ is written as $\frac{a}{b}-\frac{c}{d}$
To obtain the product of two or more rational numbers, we multiply the numerators with the numerators and the denominator with the denominators.
Product of rational numbers = $\frac{Product\, of\, the\, Numerators}{Product\,of\,the\,denominators}$
The rational number $\frac{b}{a}$ is called the multiplicative inverse or reciprocal of $\frac{a}{b}$ and is denoted by $(\frac{a}{b})^{-1}$
If $\frac{a}{b}$ and $\frac{c}{d}$ are two rational numbers such that $\frac{c}{d}\neq 0$ then the result of dividing $\frac{a}{b}$ by $\frac{c}{d}$ is the rational number obtained on multiplying $\frac{a}{b}$ by the reciprocal of $\frac{c}{d}$.
$\frac{a}{b}/\frac{c}{d}=\frac{a}{b}\times \frac{d}{c}$

Recommended Worksheets

Solving Word Problems Involving Rational Numbers 7th Grade Math Worksheets
Converting Rational Numbers to Decimals Using Long Method 7th Grade Math Worksheets
Solving Linear Equations in One Variable Integral Coefficients and Rational Coefficients 8th Grade Math Worksheets

Browse All Worksheets

We spend a lot of time researching and compiling the information on this site. If you find this useful in your research, please use the tool below to properly link to or reference Helping with Math as the source. We appreciate your support!