What are Irrational numbers?

We have learnt about decimal numbers. We also know that decimal numbers can be terminating or non-terminating. But are there any other decimal numbers other than these two categories? Let us find out.

Suppose we have a number 0.101001000100001…….

If we observe this number, we will find out in this decimal expression, on the right of the decimal point there are either 1’s or 0’s and that the 1’s are separated respectively by one zero, two zeros, three zeros and so on. Thus the number of zeros separating two successive 1’s goes on increasing by one. It can be seen that we can go on writing this number in an endless manner. This shows that the expansion of this decimal is non-terminating as well as non-repeating. Hence, it cannot be represented as a rational number as a rational numbr is either terminating or non-terminating and non-recurring.

So, what do we call such numbers?

There are infinitely many decimal numbers of the type that has been discussed above such as 0.121121112…….., 0.020020002…….m 0.3000300003……… which are non-terminating and non-recurring decimals. We say that the decimal expansion which is non-terminating and non-repeating, by definition, represents an “irrational number”.

Thus, a number is irrational if and only if its decimal representation is non-terminating and non-repeating.

 Do you know that the numbers such as , $\sqrt{2}, \,\sqrt{3}$ etc. are all irrational numbers. For example, $\sqrt{2}$ = 1.4142135…….., $\sqrt{3}$ = 1.7320508……. An irrational number is a non-terminating and non-recurring decimal, that is, it cannot be written in the form of $\frac{p}{q}$, where p and q are both integers and q ≠ 0.

Now, let us find the square root of 2.

We can see that $\sqrt{2}$ has non-terminating and non0recirring decimal expansion and it is given by 1.4142135…….

Now let us find the square root of 3.

Similarly, $\sqrt{5}, \,\sqrt{6}$ and other such square roots can also be expressed as non-terminating and non-repeating decimals and therefore they are all irrational numbers.

It is important to note here that an irrational number can be approximated as closely as we like by rational numbers.

The process of finding the square root of 2 by the division method can give us the decimal representation of $\sqrt{2}$. This can also be done using the following elementary method:

 We know that 1² = 1 < 2 < 4 = 2²

Taking positive square roots, we get 1 < $\sqrt{2}$ < 2

Next, (1.4)² = 1.96 < 2 < 2.25 = (1.5)²

Taking positive square roots again we get 1.4 < $\sqrt{2}$ < 1.5

Further, (1.41)² = 1.9881 < 2 < 2.0.164 = (1.42)²

Again, taking positive square roots we get 1.41 < $\sqrt{2}$ < 1.42

By continuing in this manner, the next step leads us to the following inequalities:

1.414 < $\sqrt{2}$ < 1.415

If we proceed in this manner, every step will give us a closer decimal approximation of $\sqrt{2}$ than in the previous step. The eighth step will give us the following inequalities:

(1.4142315)² = 1.99999982358225 < 2 < 2.00000010642496 = (1.4142316)²

This is a very close approximation of $\sqrt{2}$. Since V is not a rational number, this process will not terminate and will lead to decimal expansion, which will be non-terminating and non-repeating. Hence, the non-repeating decimal expansion of $\sqrt{2}$ will be given by $\sqrt{2}$ = 1.4142135…. where the dots indicate that this decimal representation will not terminate.

Hence,

$\sqrt{2}$ = 1.4142135……

Similarly, we can find the value of other square roots which are irrational numbers.

Notation for Irrational Numbers

The common number sets such as the natural numbers, whole numbers, real numbers etc. all have standard symbols that are used to denote them. For instance, we use N for natural numbers, R for real numbers, W for whole numbers, Z for integers and so on. Do we have such a notation of irrational numbers?

There is no standard notation for the set of irrational numbers, but the notations where the bar, minus sign, or backslash indicates the set complement of the rational numbers over the reals R could all be used such as (R – Q).

Surds

When we can’t simplify a number to remove a square root (or cube root etc,) then it is a surd. For example, √2 (square root of 2) can’t be simplified further so it is a surd.

Properties of Irrational Numbers

Irrational numbers are known to have the following properties:

1. Negative numbers of an irrational number is an irrational number.
2. If r is a rational number and s is an irrational number, then r + s and r – s are irrational numbers and rs and r/s are also irrational numbers. This means that any operation between a rational and an irrational number, be it addition, subtraction, multiplication or divisions will always result in an irrational number only.
3. If r is one irrational number and s is another irrational number, then r + s and r – s may or may not be irrational numbers and rs and r/s are may or may not be irrational numbers. This means that any operation between two irrational numbers, be it addition, subtraction, multiplication or divisions will not always result in an irrational number.
4. If a and b are two distinct positive rational numbers such that ab is not a perfect square of a rational number, then $\sqrt{ab}$ is an irrational number lying between a and b.
5. If a and b are two distinct positive irrational numbers, then $\sqrt{ab}$ is an irrational number lying between a and b.
6. Irrational numbers are always real numbers.
7. Irrational numbers consist of non-terminating and non-recurring decimals.
8. For any two irrational numbers, their least common multiple (LCM) may or may not exist.

Famous Irrational Numbers

Some irrational numbers are quite famous as they are used in everyday calculations and in basic mathematics as well. Let us learn about these famous irrational numbers.

1. The first such famous irrational number is Pi (π). People have calculated Pi to over a quadrillion decimal places and still, there is no pattern. The first few digits look like this: 3.1415926535897932384626433832795. It is defined in Euclidean geometry as the ratio of a circle’s circumference to its diameter, and also has various equivalent definitions. The number appears in many formulas in all areas of mathematics and physics. The earliest known use of the Greek letter π to represent the ratio of a circle’s circumference to its diameter was by Welsh mathematician William Jones in 1706.[1] It is also referred to as Archimedes’s constant.

• Another famous irrational number is e (Euler’s number).  The first few digits of e are 2.7182818284590452353602874713527. Euler’s number is the base of a natural logarithm. This number was first introduced in 1731 by the Swiss mathematician Leonhard Euler. It is also known as Napier Number which is frequently used in trigonometry as well as logarithms.
• The Golden Ratio number is another famous irrational number. The symbol for the golden ratio number is the Greek letter “phi” Φ. It is a special number approximately equal to 1.618.
• $\sqrt{2}$ that is so commonly sued in everyday calculations is another famous irrational number. It is also known as Pythagoras’s constant.

Commonly used Irrational Numbers

Below we have a list of commonly sued irrational numbers and their approximate values that prove helpful for mathematical calculations.

Irrational Number	Approximate Value
$\sqrt{2}$	1.414
$\sqrt{3}$	1.732
$\sqrt{5}$	2.236
π	3.14
e	2.718
$\sqrt{7}$	2.645

Difference between Rational and Irrational Numbers

Now that we know about both rational well as irrational numbers, we can clearly explain the difference between them. Some of the major differences between rational and irrational numbers include –

Rational Numbers	Irrational Numbers
Rational numbers can be expressed in the form of a fraction or ratio i.e. p/q, where q ≠ 0.	Irrational numbers cannot be expressed in the form of a fraction or ratio.
Rational numbers refer to a number that can be expressed in a ratio of two integers.	An irrational number is one that can’t be written as a ratio of two integers.
Rational numbers include perfect squares	Irrational numbers include Surds
Rational numbers are finite or recurring decimals. This means that The decimal expansion is terminating or non-terminating recurring (repeating)	Irrational numbers are non-finite or non-recurring decimals. This means that The decimal expansion is non-terminating and non-recurring at any point.
Example  – 5/8, 0.65	Example $-\sqrt{2}, \sqrt{3}$,
In rational numbers, both numerator and denominator are whole numbers, where the denominator is not equal to zero.	An irrational number cannot be written in a fraction.

Fun Facts about Irrational Numbers

1. It was Hippasus who was one of the students of Pythagoras who discovered irrational numbers. He discovered it when he was trying to write the square root of 2 as a fraction which is believed that he was doing it using geometry. While doing it, instead he proved the square root of 2 could not be written as a fraction, and therefore should be termed as irrational. However, the other followers of Pythagoras could not accept the existence of irrational numbers, and it is said that Hippasus was drowned at sea as a punishment from the gods!
2. Greek mathematicians termed this ratio of incommensurable magnitudes alogos, or inexpressible. However, Hippasus was not credited or appreciated for his explanation.
3. Theodorus of Cyrene did prove the irrational nature of the surds but it could do so only up to the whole number 17.

Rationalisation

Now we understand both rational and irrational numbers. We are aware of the techniques to solve compute values using rational numbers. If irrational numbers are present in the numerator of a fraction, we can do the calculations. But when these irrational numbers exist in denominators of fractions, they make calculations more difficult and complicated. To avoid such complications in the numeric calculations, we use the method of rationalization. Hence, rationalization can be defined as the process by which we eliminate radicals present in the denominators of fractions. So, how do calculate when we have irrational numbers in the denominator?

It is important to note here that If a surd or surd with rational numbers is present in the denominator of an equation, to simplify it or to omit the surds from the denominator, rationalization of surds is used. Surds are irrational numbers but if multiply surd with a suitable factor, the result of multiplication will be a rational number. This is the basic principle involved in the rationalization of surds.

In other words, the process of reducing a given surd to a rational form after multiplying it by a suitable surd is known as rationalization.

So, what are the steps involved in rationalisation? Let us find out.

Before understanding the steps, it is important to understand the meaning of the term “conjugate”. A conjugate is a similar surd but with a different sign. For example, the conjugate of $\sqrt{2}+\sqrt{3}$ would be $\sqrt{2}-\sqrt{3}$. Similarly,

1. The conjugate of (5 + 7–√7) is (5 – 7–√7)
2. The conjugate of (5 – 7–√7) is (5 + 7–√7)
3. The conjugate of (10 + 3–√3) is (10 – 3–√3)
4. The conjugate of (10 – 3–√3) is (10 + 3–√3)

We now understand what conjugates are, let us check how we are supposed to rationalise an irrational number.

There are two methods of rationalisation of irrational numbers. These two methods are:

1. Conjugate Method
2. Long Division Method

Let us now understand these two methods in detail.

Conjugate method

This method comes into place when we have an irrational number in the denominator. The following steps are followed for rationalising in this case:

1. Our first step is to remove the radicals from the denominator. To do this, we multiply the numerator and the denominator by a suitable conjugate.
2. Next, we need to make sure that all the surds in the given fraction are in their simplified form.
3. The last step of rationalisation is to simplify the fraction if required.

Let us understand this through an example

Example

Suppose we want to rationalise $\frac{1}{4+\sqrt{2}}$.

Solution

Let us perform the steps that have been listed above for rationalisation.

First, we need to find the conjugate of the denominator.

The denominator is $4+\sqrt{2}$. Its conjugate will be $4-\sqrt{2}$. Therefore, we will multiply both the numerator and the denominator by $4-\sqrt{2}$. We will get:

$\frac{1}{4+\sqrt{2}}\times \frac{4-\sqrt{2}}{4-\sqrt{2}}=\frac{4-\sqrt{2}}{4^{2}-\sqrt{2}^{2}}$

$=\frac{4-\sqrt{2}}{16-2}$

$=\frac{4-\sqrt{2}}{14}$

Therefore, the required rationalized number is $\frac{4-\sqrt{2}}{14}$ which is in its simplest form.

Long Division Method

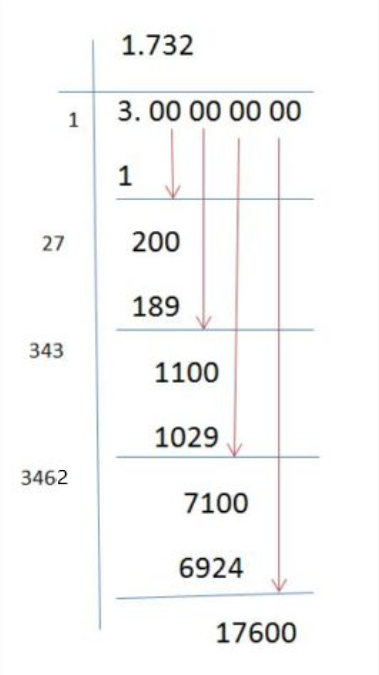
The Long Division method is the same method we use to find the square root of a number, whether rational or irrational. A limitation of this method is that it is only checking an irrational number that has the power of $\frac{1}{2}$.

So, we recall the long division we have just done for checking whether $\sqrt{3}$ is a rational or an irrational number.

Solved Examples

Example 1    

Prove that √5 is an irrational number.

Solution              

Let us prove this by the method of contradiction-
Say, √5 is a rational number. It can be expressed in the form p/q where p,q are co-prime integers.

⇒√5=p/q
⇒5=p²/q²  {Squaring both the sides}
⇒5q²=p²  (1)
⇒p² is a multiple of 5. {Euclid’s Division Lemma}
⇒p is also a multiple of 5. {Fundamental Theorem of arithmetic}
⇒p=5m
⇒p²=25m²   (2)

From equations (1) and (2), we get,

5q²=25m²
⇒q²=5m²
⇒q² is a multiple of 5. {Euclid’s Division Lemma}
⇒q is a multiple of 5. {Fundamental Theorem of Arithmetic}

Hence, p,q have a common factor 5. which contradicts that they are co-primes.  Therefore, p/q is not a rational number.

This proves that √5 is an irrational number. 

Example 2    

Find an irrational number between $\sqrt{2}$ ​and $\sqrt{3}$.

Solution              

An irrational number between $\sqrt{2}$​ and $\sqrt{3}$ is $\sqrt{\sqrt{2\times \sqrt{3}}}=\sqrt{\sqrt{6}}=6^{\frac{1}{4}}$

Example 3    

Rationalize $\frac{1}{\sqrt{5}}$.

Solution              

Since √5 is an irrational number and is present in the denominator of the fraction. So, we first need to rationalize it. This can be done by multiplying both numerator and denominator by √5.

We will get

$\frac{1}{\sqrt{5}}\times \frac{sqrt{5}}{sqrt{5}}$

$\frac{sqrt{5}}{5}$

Hence, the rationalised form of $\frac{1}{\sqrt{5}}$ is $\frac{sqrt{5}}{5}$.       

Remember

1. A number is irrational if and only if its decimal representation is non-terminating and non-repeating.
2. There is no standard notation for the set of irrational numbers, but the notations where the bar, minus sign, or backslash indicates the set complement of the rational numbers over the reals R could all be used such as (R – Q).
3. A conjugate is a similar surd but with a different sign.
4. The conjugate or the rationalizing factor of (√a +√b) is (√a -√b).
5. Each irrational number can be expressed as an infinite decimal expansion with no regularly repeating digit or group of digits. Together with the rational numbers, they form the real numbers.
6. Irrational numbers are always real numbers.
7. Irrational numbers consist of non-terminating and non-recurring decimals.
8. For any two irrational numbers, their least common multiple (LCM) may or may not exist.

Recommended Worksheets

Understanding Irrational Numbers 8th Grade Math Worksheets
Rounding Whole Numbers and Decimals (Basketball Themed) Worksheets
Solving Word Problems Involving Rational Numbers 7th Grade Math Worksheets