Prime Numbers | Definition, Examples, Properties, Gaps, Patterns

Introduction

One of the branches of mathematics, namely number theory, deals with the properties of numbers. The origins of number theory date back to antiquity, when ancient scientists mostly worked only with natural numbers. For example, anyone who is at least remotely familiar with mathematics has heard of the Pythagorean theorem and the Pythagorean triples. Many famous problems in number theory are still relevant. Number theory also studies the properties of prime numbers. To date, there are many open problems related to prime numbers, the solution of which will bring worldwide fame. So, let’s get acquainted with prime numbers.

Definition of prime and composite numbers

A prime number is a natural number that is evenly divisible only by 1 and the number itself. If a number is evenly divisibly by more than two natural numbers, then this number is a composite number.

Recall that a factor of a number is the number that divides evenly the given number. Often, if a number has only two factors, 1 and itself, it is said the number has only two trivial factors. So, all prime numbers have only two trivial factors.

Number 1 has the only one factor, so that is why it is neither prime, nor composite number. The smallest prime number is the number 2. This prime number is the only one even prime number.

EXAMPLE: 7, 17, 27, 43, 53, 63, 73, 77

Write the numbers in the table below. Explain each step.

Prime numbers	Composite numbers

SOLUTION: Let’s check which number has only trivial factors and which does not. It’s easy to see that

27=3×9

63=7×9

77=7×11

So, these numbers are composite numbers.

Dividing by all consecutive natural numbers that do not exceed this number, we can see that numbers 7, 17, 43, 53, 73 are prime numbers – they have only two factors, 1 and the number itself.

Prime numbers	Composite numbers
7, 17, 43, 53, 73	27, 63, 77

So far, we have solved this example more intuitively. Even for the number 43, it becomes difficult to check whether it is prime or composite. Is there an easier way to determine whether a number is a prime number or not?

The Sieve of Eratosthenes

Nearly 2200 years ago, ancient scientist Eratosthenes designed a clever way to find all the prime numbers up to a given number. His method of finding prime numbers is based on the idea of sieving the composite numbers from the prime numbers and is called the Sieve of Eratosthenes.

Write down all prime numbers up to 100 sifting composite numbers. Start with the rectangular table of natural numbers from 2 to 100. Circle the first prime number 2 and cross out all even numbers (numbers evenly divisible by 2).

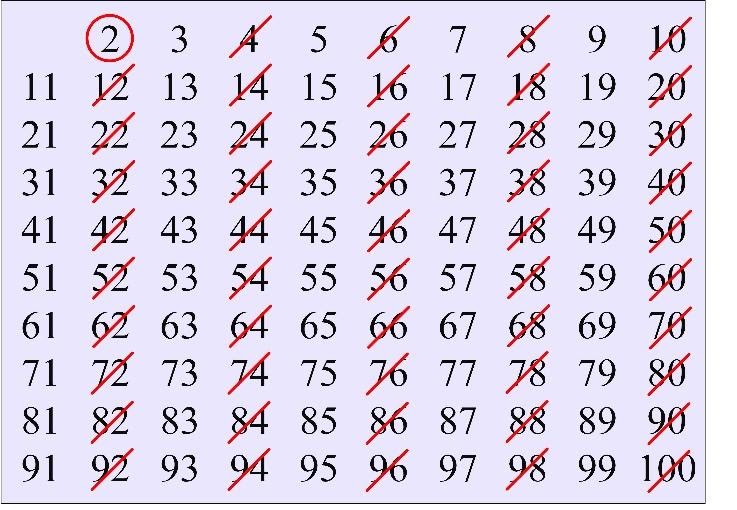
Circle the next not circled number 3 and cross out all numbers evenly divisible by 3 (every third number after 3). If it happens that the number is already crossed out (for example, the even number 6), then just skip it and move on to the next number evenly divisible by 3.

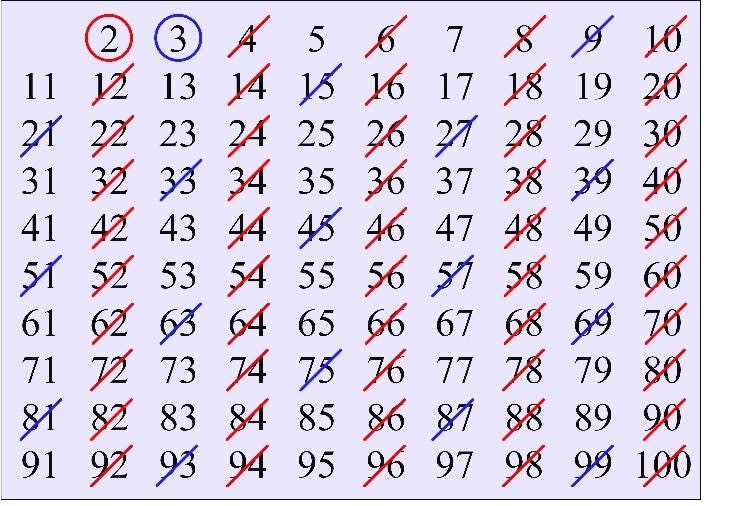
Now, circle the next not circled number 5 and cross out all numbers evenly divisible by 5 (every fifth number after 5). If it happens that the number is already crossed out (for example, the numbers 10 and 15), then just skip them and move on to the next number evenly divisible by 5.

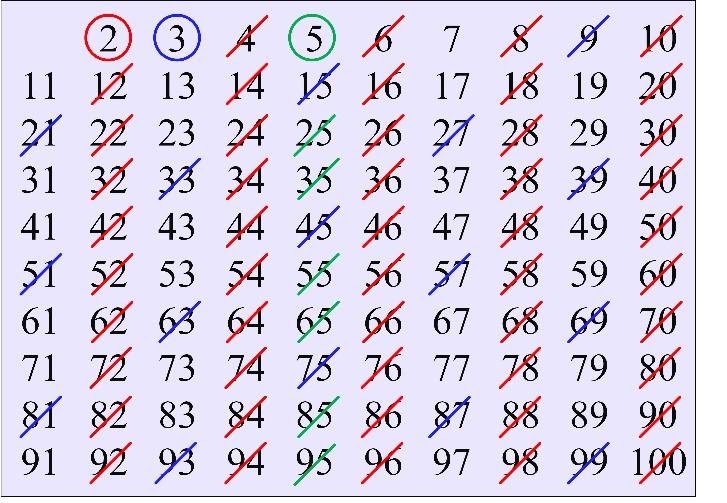
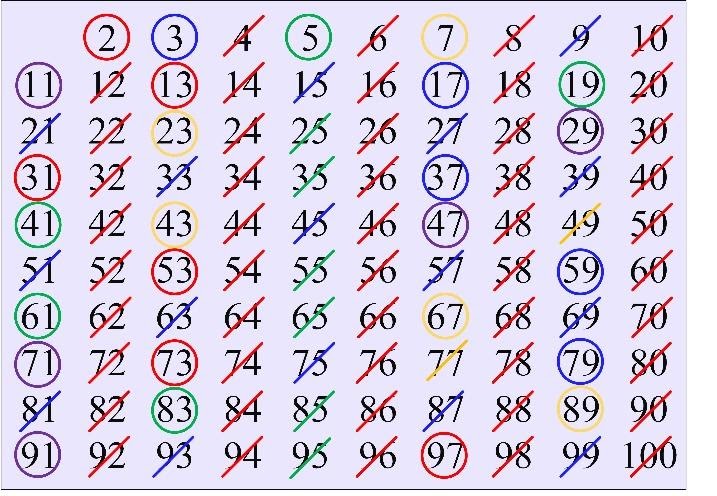
Continue crossing numbers until all numbers appear to be circled or crossed out. Circled numbers are prime and numbers crossed out are composite numbers from 1 to 100.

Prime numbers up to 1,000

By sieving composite numbers, we can write down larger prime numbers too. In fact, this has long been done and recorded in the following table.

Table of prime numbers up to 1,000

	2	3	5	7	11	13	17	19	23
29	31	37	41	43	47	53	59	61	67
71	73	79	83	89	97	101	103	107	109
113	127	131	137	139	149	151	157	163	167
173	179	181	191	193	197	199	211	223	227
229	233	239	241	251	257	263	269	271	277
281	283	293	307	311	313	317	331	337	347
349	353	359	367	373	379	383	389	397	401
409	419	421	431	433	439	443	449	457	461
463	467	479	487	491	499	503	509	521	523
541	547	557	563	569	571	577	587	593	599
601	607	613	617	619	631	641	643	647	653
659	661	673	677	683	691	701	709	719	727
733	739	743	751	757	761	769	773	787	797
809	811	821	823	827	829	839	853	857	859
863	877	881	883	887	907	911	919	929	937
941	947	953	967	971	977	983	991	997

This table makes it easy to determine whether a number is a prime or composite – just look for it among the numbers listed:

if it is present in the table – it is a prime number,

if it is absent in the table – it is a composite number.

For example, number 677 is a prime number (it is in the table) and number 899 is a composite number (it is not in the table). In fact, it is a little difficult to verify whether 899 is a prime number because it is a product of two quite large prime numbers 899=29×31, so if we started dividing by all the prime factors from 2 to the first factor of 899, it would take a long time. So, if you have a table of prime numbers – do not hesitate to use it. You use calculators or other achievements in mathematics, don’t you?

How many prime numbers are?

Nearly 2300 years ago, Euclid supposed that “Every natural number can be written as a product of prime numbers.” This statement proves another mathematical fact “There are infinitely many prime numbers”.

Let’s try to explain why this is true. Suppose there is a finite number of prime numbers. If there is a finite number of prime numbers, then there must be the greatest number. Let n be the greatest prime number. Denote m the number 2×3×5×….×n+1 – a number greater than the product of all prime numbers by 1. Divide number m by all prime numbers 2, 3, …, n.

Divide m by 2. Since the product 2×3×5×….×n is evenly divisible by 2, then the remainder from the division of the number m by 2 is 1.
Divide m by 3. Since the product 2×3×5×….×n is evenly divisible by 3, then the remainder from the division of the number m by 3 is 1.
…
Divide m by n. Since the product 2×3×5×….×n is evenly divisible by n, then the remainder from the division of the number m by n is 1.

This means that the number m is not evenly divisible by any prime number, so the number m is a prime number too, and our assumption that the number of prime numbers is finite is incorrect.

Gaps between prime numbers

If we look at the table of prime numbers, we can see quite large gaps between two adjacent prime numbers. For example, the distance between 509 and 521 is 12, the distance between 839 and 853 is 14. Are there any restrictions on the size of these gaps? Can the gaps be as large as we want?

Let’s try to do such a trick. Take some natural number n and consider the following natural numbers

n!+2, n!+3, …, n!+n,

where n!=1×2×3×…×n.

Number n!+2=1×2×3×…×n+2 is evenly divisible by 2;
Number n!+3=1×2×3×…×n+3 is evenly divisible by 3;
…
Number n!+n=1×2×3×…×n+n is evenly divisible by n.

This means all consecutive n-1 natural numbers n!+2, n!+3, …, n!+n are composite numbers and there are no prime numbers among these natural numbers. So, we constructed the interval which does not contain prime numbers (“gap” between two prime numbers). By taking n as large as we need, we will have the gap between prime numbers of the needed length.

Properties of prime numbers

FUNDAMENTAL THEOREM OM MATHEMATICS: Every natural number n>1 can be expressed as the product of one or more prime numbers, uniquely up to the order in which they appear.

From this theorem follows several important corollaries, which we will write in the form of properties of prime numbers.

PROPERTY 1: Every natural number n>1 has at least one prime factor.

PROOF: For every natural number n>1 there are two possibilities:

The number is prime.
The number is composite.

If the number is prime, then it has the only one prime factor – the number itself. If the number is composite, then it can be expressed as a product of prime factors and therefore has at least one prime factor different than the number itself.

PROPERTY 2: Every composite natural number n has at least one prime factor p such that p≤√n.

PROOF: Since number n is a composite number, then n can be expressed as a product of two or more prime non-trivial factors. Assume n=ab. Both of these factors cannot be greater than √n because then n=ab>√n√n=n. So, one of these factors is less than √n and we do not need to find factor b as these two factors form a factor pair.

This property allows us to reduce the number of steps needed to find non-trivial prime factors of a natural number n. If all prime numbers that do not exceed √n are not factors of number n, then all prime numbers greater than √n are not factors of number n too.

PROPERTY 3: If a prime number p divides a product ab of two natural numbers a and b, then it divides at least one of the factors a, b.

PROOF: This property is also known as Euclid’s lemma. Let us explain why this property holds as Euclid explained it.

Prove this property by contradiction. Assume that a prime number p that divides a product ab of two natural numbers a and b, divides neither a, nor b. If prime number p does not divide number a, then the greatest common factor between these numbers is 1 and by Euclid’s algorithm, there exist such numbers s and t that

sa+tp=1

Similarly, there exist such numbers x and y for which

xb+yp=1

Multiply these two equalities:

(sa+tp)(xb+yp)=1

sxab+syap+txbp+typ2=1

(sx)ab+(sya+txb+typ)p=1

We obtain there exist two such numbers M=sx and N=sya+txb+typ for which

Mab+Np=1

This means the greatest common factor between numbers ab and p is 1 that is a contradiction.

Why this property is helpful? Suppose we have number 27 405. Using divisibility rules, we know this number is evenly divisible by 5 (end with 5) and by 9 (the sum of the digits 2+7+4+0+5=18 is evenly divisible by 9). So, at least one of the factors of number 27 405 is evenly divisible by 5 and one is evenly divisible by 9.

Patterns with prime numbers

Many mathematicians from ancient times to the present have studied prime numbers. As a result, many interesting facts about prime numbers have been discovered. For example, is it possible to describe all prime numbers by a single formula? Are there any patterns in the appearance of prime numbers?

FACT 1: Leonard Euler proved that for all natural numbers from 1 to 40, the numbers described by a quadratic trinomial x2+x+41 are prime. Don’t you believe? Try to substitute some number from 1 to 40, or even all numbers in turn, and make sure it will. For example, we will demonstrate it for number 13:

13²+13+41=169+13+41=223

Number 223 is in the table of prime numbers, so it is a prime number.

Oh, you can say it appears prime because number 13 is prime. Then try to substitute some composite number, for example 24:

24²+24+41=576+24+41=641

Not surprisingly, this number is also in the table of prime numbers, so it is a prime number too.

But if you substitute the number 41 in this quadratic polynomial, the result will be a composite number. In general, many scientists have investigated whether a polynomial can describe the set of all prime numbers. It is currently proven that there is no non-constant polynomial that will take only prime values, but it is still not proven whether there is a non-linear polynomial, among the values of which will be an infinite number of prime numbers.

One might think that polynomials of the form x²+x+p, where p is prime, always take prime values for all natural numbers less than p, but this is not true. For example, for a polynomial x²+x+47, if we take x=12, the result

12²+12+47=144+12+47=203=7×29

is a composite number.

FACT 2: All prime numbers can be found among the natural numbers given by formulas 6n-1 or 6n+1. Interesting fact? Let’s check some prime numbers. Start with the small numbers:

7=6+1

11=6⋅2-1

Good, now check some greater numbers:

41=6⋅7-1

97=6⋅16+1

And two large numbers:

619=6⋅103+1

941=6⋅157- 1

This fact is very well graphically illustrated for all prime numbers from 2 to 100.

PATTERN 1: Write the numbers from 2 to 100 in six columns as shown in the figure. At the beginning of each column, circle the number if it is prime and cross out the whole column if the number at the beginning is composite. Cross out the columns under numbers 2 and 3. Also cross out all numbers standing on the diagonals that are evenly divisible by 5 and 7. Al remaining numbers are prime numbers. Numbers under 7 are of the form

6n+1 and numbers under 5 are of the form 6n-1.

On a sample of numbers this diagram shows that not all numbers of the form 6n+1 or 6n-1 are prime, but there are no other prime numbers.

PATTERN 2: Once, during a boring report, Stanislav Ulam had

fun drawing natural numbers in a spiral and circling only prime

numbers. It turned out that there is a certain pattern in the placement

of prime numbers. Now this pattern is called Ulam spiral.

For the first 100 numbers this spiral is shown in the diagram below.

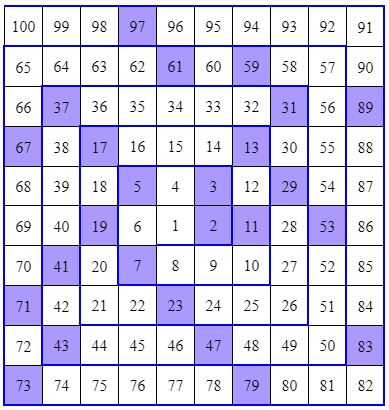
When Ulam began to study this pattern, he noticed that for a large number of prime numbers, the spiral becomes more visible.

Picture taken from online calculator

There is one wonderful feature in Ulam spiral – you can find quite long chain of prime numbers located diagonally. One of these chains is shown in the figure below – this is part of the table above.

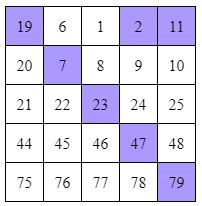
In general, prime numbers are very good at “drawing patterns”. It is possible that you will be able to invent some personal pattern of prime numbers.

Quiz

Which of the following numbers are prime?

2322, 3407, 7777

SOLUTION: It is easy to see that numbers 2322 and 7777 are composite numbers.

Number 2322 is an even number, so it is a composite number.

Since number 7777=7×1111 has the prime factor 7, then this number is a composite number too.

To check whether the number √3407 is a prime number, you need to check its divisibility by all prime numbers up to 3407≈58.

3407÷2=1703 r.1

3407÷3=1135 r.2

3407÷5=681 r.2

3407÷7=486 r.5

3407÷11=309 r.8

3407÷13=262 r.1

3407÷17=200 r.7

3407÷19=179 r.6

3407÷23=148 r.3

3407÷29=117 r.14

3407÷31=109 r.28

3407÷37=92 r.3

3407÷41=83 r.4

3407÷43=79 r.10

3407÷47=72 r.23

3407÷53=64 r.15

Therefore, number 3407 is not evenly divisible by any prime number from 2 to √3407 and is a prime number.

ANSWER: Numbers 2322 and 7777 are composite numbers, number 3407 is a prime number

Construct an interval of length at least 12 that does not contain prime numbers.

SOLUTION: From the article we know that interval from n!+2 to n!+n does not contain prime numbers and has the length of n-1. So, if n-1=13, then between numbers 13!+2 and 13!+13 has no prime numbers. Actually,

13!=1×2×…×13=6 227 020 800

So, between numbers 6 227 020 802 and 6 227 020 813 there no prime numbers.

Note, you can find another interval without prime number in different way. For example, between prime numbers 839 and 853 (the length of this gap is 13) there are no prime numbers too. However, the algorithm used is universal.

Find the smallest composite number of the form n²-n+17.

SOLUTION: Start from the smallest natural number and finfish when the value of the quadratic polynomial is prime.

n=1: 1²-1+17=17 – prime

n=2: 2²-2+17=19 – prime

n=3: 3²-3+17=23 – prime

n=4: 4²-4+17=29 – prime

n=5: 5²-5+17=37 – prime

n=6: 6²-6+17=47 – prime

n=7: 7²-7+17=59 – prime

n=8: 8²-8+17=73 – prime

n=9: 9²-9+17=89 – prime

n=10: 10²-10+17=107 – prime

n=11: 11²-11+17=127 – prime

n=12: 12²-12+17=149 – prime

n=13: 13²-13+17=173 – prime

n=14: 14²-14+17=199 – prime

n=15: 15²-15+17=227 – prime

n=16: 16²-16+17=257 – prime

Obviously, for n = 17 it will already be a composite number, because

17²-17+17=17²

is a perfect square.

ANSWER: 17

If p is a prime number, can the numbers p, p+3, p+6 be prime at the same time?

SOLUTION: If p=2, then three listed numbers are 2, 5, 8. Number 8 is a composite number, so in this case numbers p, p+3, p+6 cannot be prime at the same time.

If p>2, then p is an odd number and number p+3 is an even number greater than 2. So, p+3 is a composite number. Hence, in this case numbers p, p+3, p+6 cannot be prime at the same time too.

This means for all prime numbers p, three numbers p, p+3 and p+6 are never prime at the same time.

ANSWER: No

If p>2 is a prime number, prove that p²-9 is evenly divisible by 8.

SOLUTION: If a prime number p is greater than 2, then p is an odd number.

Consider number p²-9. We know that p²-9=(p-3)(p+3). If p is odd umber, then p-3 and p+3 are both even numbers.

Writhe the list of consecutive natural numbers from p-3 to p+3:

p-3, p-2, p-1, p, p+1, p+2, p+3

(even, odd, even, odd, even, odd, even)

One of the two numbers p-3 and p-1 is evenly divisible by 4 because one of two consecutive numbers is always evenly divisible by 4. If this number is p-3, then the product (p-3)(p+3) is evenly divisible by 4×2=8. If number p-3 is not evenly divisible by 4, then number p-1 is evenly divisible by 4 and the next even number evenly divisible by 4 is number p+3. Therefore, the product p-3(p+3) is evenly divisible by 2×4=8 too.

Conclusions

A prime number has only two factors – number 1 and the number itself.
A composite number always has more than two factors.
Number 1 is not a prime number.
The smallest prime number is 2.
The only even prime number is number 2.
Prime numbers are still of interest to mathematicians. Some of the open problems called “hypotheses” are related to prime numbers. Whoever solves such an open problem, will get $1,000,000.
Prime numbers have great practical application: computer algorithms, cybersecurity, cryptocurrency – all this is based on the theory of prime numbers.

Recommended Worksheets

Prime Numbers (Diwali Themed) Math Worksheets
Prime and Composite Numbers (Halloween Themed) Worksheets
Prime and Composite Numbers 4th Grade Math Worksheets

Browse All Worksheets

We spend a lot of time researching and compiling the information on this site. If you find this useful in your research, please use the tool below to properly link to or reference Helping with Math as the source. We appreciate your support!