Introduction
When you started counting, the numbers you used—1, 2, 3, 4, 5, and so on—were natural numbers. They are called “natural” because they come naturally when we count objects or perform basic arithmetic. The basic concepts of natural numbers and their use in mathematics will be discussed in this article.
Grade Appropriateness
The concept of natural numbers is introduced in the early stages of learning, typically around 1st grade or kindergarten. However, the topic remains relevant throughout your educational journey, as natural numbers lay the foundation for other mathematical concepts like whole numbers, integers, fractions, and even more complex topics.
Math Domain
Natural numbers fall under the domain of Numbers and Operations in Base Ten. They form the foundation of arithmetic operations, number systems, algebra, and more.
Applicable Common Core Standards
The understanding and usage of natural numbers align with several Common Core Standards. Some relevant standards include:
CCSS.MATH.CONTENT.1.NBT.B.2: Understand that the two digits of a two-digit number represent amounts of tens and ones.
CCSS.MATH.CONTENT.2.NBT.A.1: Understand that the three digits of a three-digit number represent amounts of hundreds, tens, and ones.
CCSS.MATH.CONTENT.3.NBT.A.2: Fluently add and subtract within 1000 using strategies and algorithms based on place value, properties of operations, and/or the relationship between addition and subtraction.
Definition of the Topic
Natural numbers include the set of positive integers beginning from 1 and extending to infinity. It means natural numbers have 1, 2, 3, 4, 5, and so on, without end. Natural numbers do not include zero, fractions, decimals, or negative numbers.
Key Concepts
The key concepts related to natural numbers include counting, addition, subtraction, multiplication, and division. Since natural numbers are fundamental to these concepts, they also underpin more complex mathematical operations.
Discussion with Illustrative Examples
Natural numbers range from 1 to infinity and are all positive integers. As they are used to count objects, they are also known as counting numbers. 0 and negative integers are not considered to be natural numbers.
The number line below shows the set of natural numbers, which starts from 1 extending to infinity.

Let’s illustrate the concept of natural numbers:
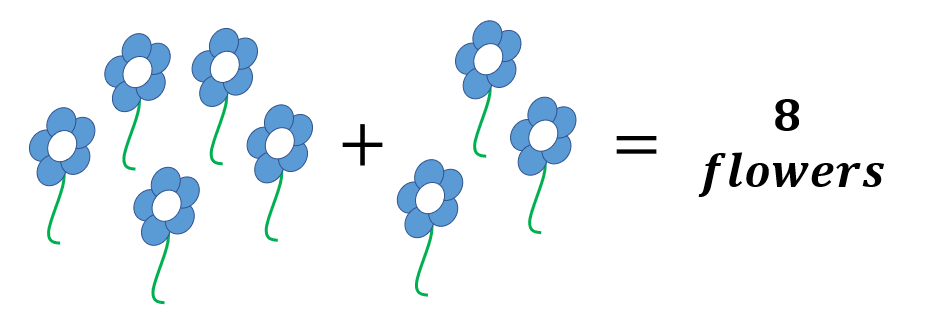
If you have five flowers and you get three more, you now have eight flowers. The numbers 5, 3, and 8 are all natural numbers.
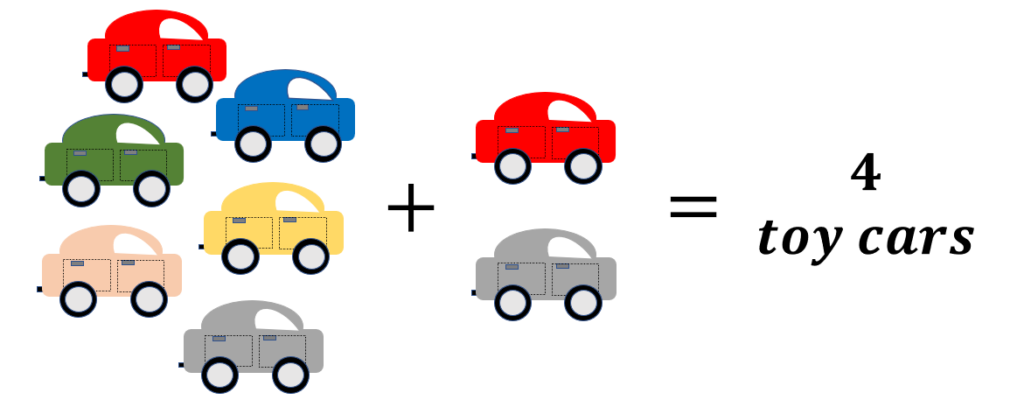
Suppose you have six toy cars and give 2 to your friend. You are now left with four toy cars. Here, 6, 2, and 4 are natural numbers.
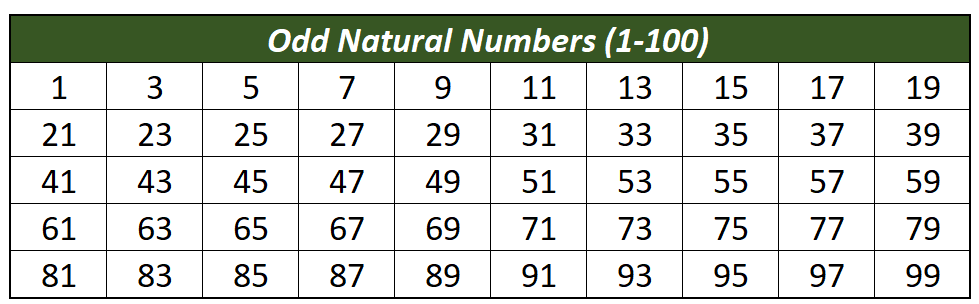
Odd Natural Numbers
Positive numbers that are not divisible by two are called odd natural numbers.
Below is a list of odd natural numbers from 1-100.
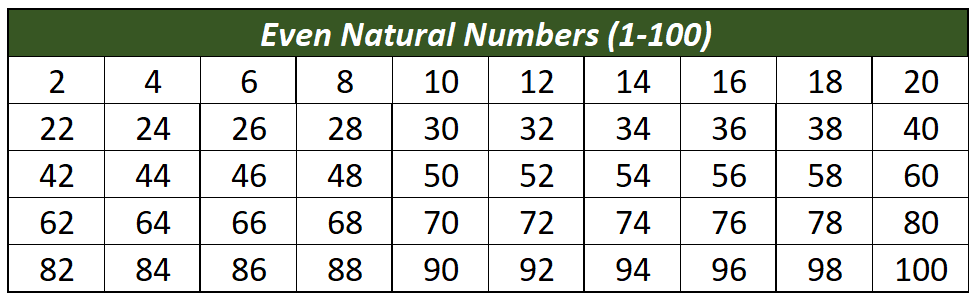
Even Natural Numbers
Positive numbers that are divisible by two are referred to as even natural numbers.
Below is a list of even natural numbers from 1-100.
Properties of Natural Numbers
The set of natural numbers includes the following properties:
Closure Property
Associative Property
Commutative Property
Distributive Property
Closure Property
The closure property of natural numbers applies only to addition and multiplication. The result will always be a natural number when you add or multiply two natural numbers.
Examples
The sum of natural numbers is a natural number.
3+4=7
5+7=12
6+11=17
The product of natural numbers is a natural number.
2×6=12
5×7=35
8×11=88
The closure property does not hold for subtraction and division since subtracting and dividing natural numbers will not always result in a natural number.
Say, for example,
8-10=-2
12÷5=2.4
Notice that -2 and 2.4 are not natural numbers.
Commutative Property
The commutative property of natural numbers applies only to addition and multiplication. The commutative property states that the sum or product of two natural numbers does not change even if we change the order of numbers.
Examples
Commutative Property of Addition
3+2=5 and 2+3=5
1+8=9 and 8+1=9
Commutative Property of Multiplication
5×2=10 and 2×5=10
3×4=12 and 4×3=12
The commutative property does not hold for the division and subtraction of natural numbers.
Associative Property
The associative property of natural numbers applies only to addition and multiplication. The sum or product natural numbers do not change even if we change the grouping of numbers.
Examples
Associative Property of Addition
(4+2)+3=9 and 4+(2+3)=9
(3+4)+6=13 and 3+(4+6)=13
Associative Property of Multiplication
(2×3)×4=24 and 2×(3×4)=24
(5×6)×2=60 and 5×(6×2)=60
For the division and subtraction of natural numbers, the associative property does not apply.
Distributive Property
The distributive property of natural numbers has the distributive law of multiplication over addition and multiplication over subtraction.
The distributive law of multiplication of natural numbers over addition states that if we multiply the sum of two natural numbers by a natural number or multiply each natural number individually and then add them, the result is the same.
Examples
3×(2+6)=(3×2)+(3×6)=24
5×(3+4)=(5×3)+(5×4)=35
The distributive law of multiplication of natural numbers over subtraction states that if we multiply the difference of two natural numbers by a natural number or multiply each natural number individually and then subtract them, the result is the same.
Examples
4×(5-2)=(4×5)-(4×2)=12
6×(7-4)=(6×7)-(6×4)=18
Examples with Solutions
Example 1
Find the sum of the natural numbers 4 and 5.
Solution
The sum is calculated by addition, so 4 + 5 = 9.
Example 2
Find the product of the natural numbers 7 and 3.
Solution
The product is calculated by multiplication, so 7 × 3 = 21.
Example 3
Which property of natural numbers holds for 5 + (4+7) = (5+4) + 7?
Solution
The associative property of addition of natural number holds for 5 + (4+7) = (5+4) + 7.
Example 4
Which property of natural numbers holds for 5×(3+7)=(5×3)+(5×7)?
Solution
The distributive property of multiplication of natural numbers over addition holds for 5×(3+7)=(5×3)+(5×7).
Real-life Application with Solution
Natural numbers play a significant role in our day-to-day lives.
For example, suppose you are saving up to buy a new video game that costs \$50. If you save \$10 each week, how many weeks will it take you to save enough money?
Solution
Divide the total amount needed (\$50) by the amount saved each week (\$10).
So, 50 ÷ 10 = 5. It will take five weeks to save enough money, where 50 and 10 are natural numbers.
Practice Test
1. Add 8 and 7.
2. Subtract two from 10.
3. Multiply three by 4.
4. Divide 20 by 5.
5. Add 12, 7, and 3.
6. Sam has ten marbles, and his friend gives him four more. How many marbles does Sam have now?
7. Lucy had 15 apples. She gave five apples to her friend. How many apples does Lucy have left?
Answers
1. 8 + 7 = 15
2. 10 – 2 = 8
3. 3 × 4 = 12
4. 20 ÷ 5 = 4
5. 12 + 7 + 3 = 22
6. 10 + 4 = 14
7. 15 – 5 = 10
Frequently Asked Questions (FAQs)
Is zero a natural number?
No, zero is not considered a natural number. The set of natural numbers starts from 1.
Are there any negative natural numbers?
No, natural numbers are always positive. They do not include any negative numbers.
Do natural numbers include fractions or decimals?
No, natural numbers do not include fractions or decimals. They are always whole numbers.
How are natural numbers used in daily life?
Natural numbers are used daily, from counting objects to calculating costs, measuring time, etc.
What comes after natural numbers in the number system?
After natural numbers, we introduce zero and create a set called whole numbers. Further, by including negative counterparts of whole numbers, we get integers.
Recommended Worksheets
Natural Numbers (Arbor Day Themed) Math Worksheets
Even and Odd Numbers (Ages 6-8) Worksheets (Labor Day Themed)
Consecutive Numbers (Diwali Themed) Math Worksheets









