Introduction
The study of mathematics includes numbers and the different patterns in which they can be represented. This means that when we think of mathematics, the first thing that comes to our mind is numbers. We are aware of different kinds of numbers that have been defined such as natural numbers, whole numbers, decimals, fractions and so on. Each set of a number has its own unique characteristic that makes it a set. For instance, the set of even numbers comprises of all numbers that are divisible by 2. Similarly, prime numbers are the numbers that are not completely divisible by any other number other than themselves and the number 1. By seeing these examples can we say that the numbers can be put in a sort of a pattern? Let us find out.
What are Number Patterns?
Number patterns are sequences of numbers that repeat themselves. In other words, patterns are a set of numbers arranged in a sequence such that they are related to each other in a specific rule.
How to Identify Number Patterns?
We are aware of the four operations of mathematical operators, namely, addition, subtraction, multiplication and division. Most of the number patterns are based on these four mathematical operations only. However, there are some patterns that involve a combination of these operations.
Let us understand this by an example.
Suppose, we have been given the number pattern 1, 3, 5, 7, 9, ………….
What arithmetic pattern is followed by the above sequence? Let us find out.
Observe each of the terms carefully. We can see that –
First Term = 1 = 2 x 0 + 1
Second Term = 3 = 2 x 1 + 1
Third Term = 5 = 2 x 2 + 1
Fourth Term = 7 = 2 x 3 + 1
Fifth Term = 9 = 2 x 4 + 1 and so on.
Therefore, we can identify the number pattern in the given sequence as 2 n + 1, where n ≥1. We can clearly see that this sequence involved a combination of two operators, “ x “ and “ + “.
Through this example, we have learnt that a number of different combinations of operators can be used to define the number pattern in a sequence.
What is a Sequence?
In mathematics, a sequence is a chain of numbers (or other objects) that usually follows a particular pattern. The individual elements in a sequence are called terms. In other words, a sequence is an ordered list of numbers (or other elements like geometric objects), that often follow a specific pattern or function. Sequences can be both finite and infinite. The terms of a sequence are all its individual numbers or elements.
Types of Number Sequences
Following are the different types of patterns that are most commonly in use when we define a sequence of numbers–
- Growing Sequence – As the name suggests, the growing sequence is the number pattern where the numbers are present in an increasing order.
- Reducing Sequence – Again, as the name signifies, a reducing sequence is the number pattern in which the numbers are present in the decreasing order.
- Recurring Sequence – In the recurring sequence of numbers, the same set of numbers keep repeating themselves to form a pattern of numbers.
Importance of Rules in Number Patterns and Sequences
There are a certain set of rules that the number patterns and sequences follow. These rules define the terms that are contained in a number pattern. We need to understand these rules in order to understand the number sequence. The understand of these rules is extremely important as without them we cannot find a missing term in the sequence or know the pattern in which the number sequence has been made.
Let us understand this by an example. Consider the following number sequence –
1, 4, 9, 16, 25, 36, ?
Now, if we wish to find which term comes after 36, we must first understand the rule that defines this number sequence.
To find rule the rule that has determined the terms of the sequence, we should observe the terms carefully. We can observe the following –
- Every term is a product of itself.
- The numbers that have been multiplied by themselves are natural numbers.
This means that –
1 = 1 x 1
4 = 2 x 2
9 = 3 x 3
16 = 4 x 4
25 = 5 x 5
36 = 6 x 6
By this order, the next term should be a multiple of 7 multiplied by itself. Therefore, we have,
7 x 7 = 49 will be the next term of the given number sequence.
Simple Sequences
Even and Odd Number Sequences
We are aware of natural numbers. Natural numbers are the numbers that begin from 1 and go on up to infinity. They are in the form of 1 , 2 , 3, 4 and so on. Natural numbers simply form two types of patterns, depending upon the fact whether they are odd or even. Recall that odd numbers are the numbers which when divided by 2 will leave 1 as a remainder. In other words, odd numbers are the numbers that are not divisible by 2. So, how is the pattern of odd numbers defined? The number pattern of odd numbers is defined by the numbers starting from 1 ,3 , 5 , 7 , 9 and so on. Mathematically, this pattern for natural numbers can also be represented as the following on a number line.
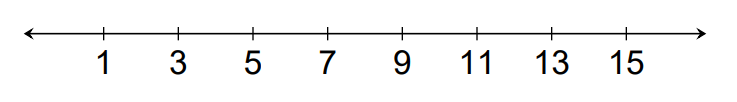
Therefore, the pattern of odd natural numbers is 1, 3, 5, 7, 9, 11 and so on.
Similarly, let us recall what we mean by even numbers. Even numbers are the numbers which when divided by 2 will leave 0 as a remainder. In other words, even numbers are the numbers that are completely divisible by 2. So, how is the pattern of even numbers defined? The arithmetic pattern of even numbers is given by 2, 4, 6, 8, 10 and so on. Mathematically, this pattern for natural numbers can also be represented on a number line as –
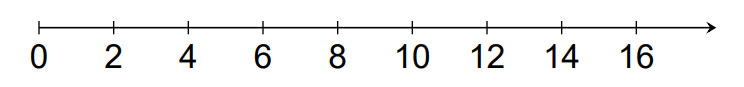
Therefore, the pattern of even natural numbers is 2, 4, 6, 8, 10, 12 and so on.
Now, let us learn about special sequences of numbers.
Sequence of Triangular Numbers
A number sequence of triangular numbers is the pattern that has triangular numbers. But, what are these triangular numbers? Let us find out. Triangular numbers are generated from a pattern of dots / boxes that form a triangle. In other words, the triangular number sequence is the representation of the numbers in the form of an equilateral triangle. The pattern formed by the triangular numbers is such that the sum of the previous number and the order of the succeeding number results in the sequence of triangular numbers. This arrangement is represented as below –
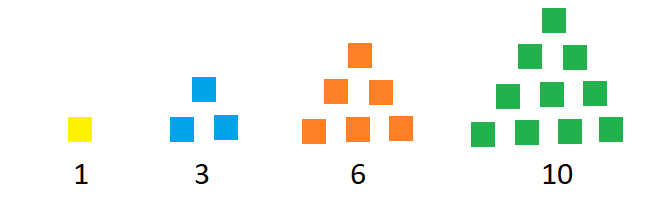
Arithmetic Number Sequences
There are two most common arithmetic sequences –
- Number Sequence of Square Numbers
- Number Sequence of Cube Numbers
Let us learn about them one by one.
Number Sequence of Square Numbers
A number sequence of square numbers is a pattern that has square numbers. But, what are these square numbers? Let us find out. Square numbers are the numbers obtained when a number is multiplied by itself. For instance 2 x 2 = 4, therefore, 4 is the square of 2. Similarly, 3 x 3 = 9, therefore, 9 is the square of 3. The number sequence of square numbers is given by 1, 4, 9, 16, 25, 36 and so on. Now, though we can easily identify the first few numbers of this pattern, how do we find a number on any position of the pattern? Can we define a formula to help us identify the number at a particular position in the number? The formula for defining the pattern of square numbers is given by
Arithmetic pattern of Square Numbers = n 2, where n ≥ 1.
Let us verify the above formula for obtaining the pattern of numbers.
If we put n = 1 in the above formula, we will get 1 2 = 1 x 1 = 1
If we put n = 2 in the above formula, we will get 2 2 = 2 x 2 = 4
If we put n = 3 in the above formula, we will get 3 2 = 3 x 3 = 9
If we put n = 4 in the above formula, we will get 4 2 = 4 x 4 = 16
If we put n = 5 in the above formula, we will get 5 2 = 5 x 5 = 25 and so on.
So, we can see that just by putting the value of the position of the number in the above formula, we can obtain the number in the pattern of square numbers.
Number Sequence of Cube Numbers
A number sequence of cube numbers is the pattern that has cube numbers. But, what are these cube numbers? Let us find out. Cube numbers are the numbers obtained when a number is multiplied twice with itself. For instance 2 x 2 x 2 = 8, therefore, 8 is the cube of 2. Similarly, 3 x 3 x 3 = 27, therefore, 27 is the cube of 3. The number sequence of cube numbers is given by 1, 8, 27, 12, 64, 125 and so on. Now, though we can easily identify the first few numbers of this pattern, how do we find a number on any position of the pattern? Can we define a formula to help us identify the number at a particular position in the number? The formula for defining the pattern of cube numbers is given by
Arithmetic pattern of Cube Numbers = n 3, where n ≥ 1.
Let us verify the above formula for obtaining the pattern of numbers.
If we put n = 1 in the above formula, we will get 1 3 = 1 x 1 x 1 = 1
If we put n = 2 in the above formula, we will get 2 3 = 2 x 2 x 2 = 8
If we put n = 3 in the above formula, we will get 3 3 = 3 x 3 x 3 = 27
If we put n = 4 in the above formula, we will get 4 3 = 4 x 4 x 4 = 64
If we put n = 5 in the above formula, we will get 5 3 = 5 x 5 x 5 = 125 and so on.
So, we can see that just by putting the value of the position of the number in the above formula, we can obtain the number in the pattern of cube numbers.
Fibonacci Number Sequences
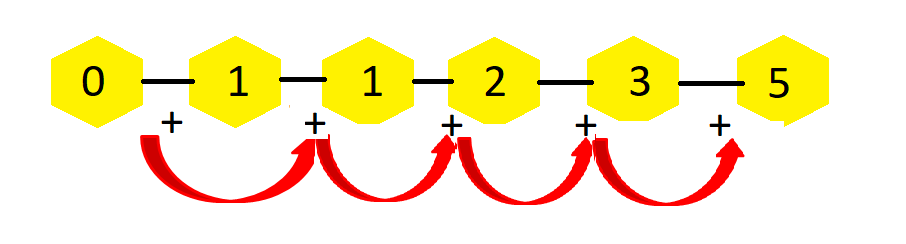
The Fibonacci number sequence is named for Leonardo Fibonacci, born in 1170 in Pisa, Italy. The Fibonacci number sequence is a sequence of numbers in which each number in the sequence is obtained by adding the two previous numbers together. The sequence starts with 0 and 1. The importance of this number sequence lies in the fact that it can be found in many things in nature such as plant leafing patterns, spiral galaxy patterns, and the chambered nautilus’ measurements. The series is thus defined as –
| First Number | 0 |
| Second Number | 1 |
| Third Number | 0 + 1 = 1 |
| Fourth Number | 1 + 1 = 2 |
| Fifth Number | 1 + 2 = 3 |
| Sixth Number | 2 + 3 = 5 and so on |
Geometric Number Sequences
In a Geometric Number Sequence each term is found by multiplying the previous term by a constant. Let us understand the geometric number sequence by an example.
Consider the following number sequence –
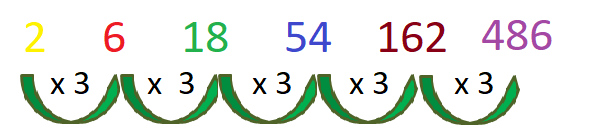
2, 6, 18, 54, 162, 486, ……..
Let us analyse each term of this number sequence. We have,
| First Term | 2 |
| Second Term | 6 = 2 x 3 |
| Third Term | 18 = 6 x 3 |
| Fourth Term | 54 = 18 x3 |
| Fifth Term | 162 = 54 x3 |
| Sixth Term | 486 = 162 x 3 |
We can notice from the above arrangement that in order to obtain the next term of the number sequence we are multiplying the previous term by 3. This means that a term when multiplied by 3 will give us the next term of the number sequence. Since, this sequence involves multiplying the previous term by a constant to obtain the next term; therefore, it is a geometric sequence.
Another important observation in the above number sequence is that every two consecutive terms share the same ratio. This means that –
$\frac{6}{2}$ = 3
$\frac{18}{16}$ = 3
$\frac{54}{18}$ = 3
$\frac{162}{54}$ = 3
$\frac{486}{162}$ = 3
Thus, we can say that there exists a common ratio between every two consecutive terms in a geometric sequence.
Solved Examples
Example 1 Determine the value of A and B in the following pattern.
15, 22, 29, 36, 43, A, 57, 64, 71, 78, 85, B.
Solution We have been given the number sequence
15, 22, 29, 36, 43, A, 57, 64, 71, 78, 85, B and we need to find the values of A and B
Let us observe each term carefully.
| First Term | 15 |
| Second Term | 22 = 15 + 7 |
| Third Term | 29 = 22 + 7 |
| Fourth Term | 36 = 29 + 7 |
| Fifth Term | 43 = 36 + 7 |
| Sixth Term | A |
Now, going by the above pattern, A should be 43 + 7 = 50
Hence, sixth term = A = 50
Now,
Similarly, B will the 7 added to the previous term.
This means that B = 85 + 7 = 92
Hence, we have, A = 50 and B = 92
Example 2 Find the missing value in the geometric pattern: 120, 60, __, 15, __.
Solution We have been given a geometric pattern and we need to find the missing terms. Let the missing terms be A and B. so, we have the number sequence as –
120, 60, A, 15, B
Now, we know that since it is a geometric sequence, therefore, the ratio of any two consecutive terms will be the same. Therefore, let us find the ratio of the first two terms. We will have,
$\frac{120}{60}$ = 2
Similarly,
$\frac{60}{A}$ = 2
A = $\frac{60}{2}$ = 30
Also,
$\frac{15}{B}$ = 2
B = $\frac{15}{2}$ = 7.5
Hence, A = 60 and B = 7.5 which completes the number sequence as
120, 60, 30, 15, 7.5
Key Facts and Summary
- Number patterns are sequences of numbers that repeat themselves.
- A sequence is a chain of numbers (or other objects) that usually follows a particular pattern.
- The individual elements in a sequence are called terms.
- Natural numbers simply form two types of patterns, depending upon the fact whether they are odd or even.
- Triangular numbers are generated from a pattern of dots/boxes that form a triangle.
- Square numbers are the numbers obtained when a number is multiplied by itself.
- Cube numbers are the numbers obtained when a number is multiplied twice with itself.
- The Fibonacci number sequence is a sequence of numbers in which each number in the sequence is obtained by adding the two previous numbers together. The sequence starts with 0 and 1.
- In a Geometric Number Sequence each term is found by multiplying the previous term by a constant.
- There exists a common ratio between every two consecutive terms in a geometric sequence.









