Composite Numbers

Introduction

Mathematics is a world of numbers. We have different types of numbers such as natural numbers, whole numbers, decimal numbers, fractions etc. that are based on certain characteristics of numbers. We use numbers in our day to day life. They are often called numerals. Without these numbers, it would be impossible to even count things. Different arithmetic operations can be performed using these numbers. Numbers can be categorised as prime as composite numbers, except 1 which is neither prime nor even. Let us learn more about composite numbers.

Definition

Composite numbers are numbers with more than two factors. In other words, composite numbers are those natural numbers that have more than 2 factors. 

What are Composite Numbers?

The number of factors that a number has is one of the manners in which the classification of numbers has been done. The numbers are classified as composite or prime based on the number of factors they have.

Every number has at least 2 factors. The first is the number 1 while the other is the number itself. For numbers that have factors other than these two, we call them composite numbers. For instance, consider the number 4. How many factors does 4 have? The factors of 4 are – 1, 2 and 4. So the number 4 has 3 factors. Therefore, 4 is a composite number. Let us consider another number, say 3. How many factors does 3 have? The factors of 3 are – 1 and 3. So the number 3 has only 2 factors. Therefore, it is not a composite number. This means that not every number is a composite number. What do we call numbers that are not composite? Let us find out.

The numbers that have only two factors, i.e. 1 and the number itself are called prime numbers. For example, consider the number 5. How many factors does the number 5 have? The factors of 5 are 1 and 5. This means that 5 has only two factors, 1 and the number 5 itself. Hence, it is a prime number.

It is important to note here that composite numbers are always natural numbers. Hence, there is no composite number which is a fraction or a decimal. Similarly, prime numbers are also always natural numbers. Hence, there is no prime number which is a fraction or a decimal.

How many Composite Numbers are there?

It can be said that there are infinitely many composite numbers. This is because we have an endless counting system and there is always a number greater than a number we can think of. Therefore, we can always have a composite number no matter how large the number is. 

List of Composite Numbers from 1 to 100

When looking at the numbers from 1 to 100, we can say that there are 74 composite numbers between 1  – 100.

Let us have a look at them – 

Composite Numbers between 1 and 10 are 4, 6, 8, 9 and 10 which makes it five composite numbers between the numbers 1 to 10.

Composite Numbers between 11 and 20 are 12, 14, 15, 16, 18 and 20 which makes it six composite numbers between the numbers 11 to 20.

Composite Numbers between 21 and 30 are 21, 22, 24, 25, 26, 27, 28 and 30 which makes it eight composite numbers between the numbers 21 and 30.

Composite Numbers between 31 and 40 are 32, 33, 34, 35, 36, 38, 39 and 40 which makes it eight composite numbers between the numbers 31 and 40.

Composite Numbers between 41 and 50 are 42, 44, 45, 46, 48, 49 and 50 which makes it seven composite numbers between the numbers 41 and 50.

Composite Numbers between 51 and 60 are 51, 52, 54, 55, 56, 57, 58 and 60 which makes it eight composite numbers between the numbers 51 and 60.

Composite Numbers between 61 and 70 are 62, 63, 64, 65, 66, 68, 69 and 70 which makes it eight composite numbers between the numbers 51 and 60.

Composite Numbers between 71 and 80 are 72, 74, 75, 76, 77, 78 and 80 which makes it seven composite numbers between the numbers 71 and 80.

Composite Numbers between 81 and 90 are 81, 82, 84, 85, 86, 87, 88 and 90 which makes it eight composite numbers between the numbers 81 and 90.

Composite Numbers between 91 and 100 are 91, 92, 93, 94, 95, 96, 98, 99 and 100 which make it nine composite numbers between the numbers 91 and 100.

Putting the above information in tabular form we have – 

Range of Numbers	Composite Numbers	Total Composite Numbers
1 – 1 0	4, 6, 8, 9, 10	5
1 1 – 2 0	12, 14, 15, 16, 18, 20	6
2 1 – 3 0	21, 22, 24, 25, 26, 27, 28, 30	8
3 1 – 4 0	32, 33, 34, 35, 36, 38, 39, 40	8
4 1 – 5 0	42, 44, 45, 46, 48, 49, 50	7
5 1 – 6 0	51, 52, 54, 55, 56, 57, 58, 60	8
6 1 – 7 0	62, 63, 64, 65, 66, 68, 69, 70	8
7 1 – 8 0	72, 74, 75, 76, 77, 78, 80	7
8 1 – 9 0	81, 82, 84, 85, 86, 87, 88, 90	8
9 1 – 1 0 0	91, 92, 93, 94, 95, 96, 98, 99, 100	9

Composite Numbers Chart

In the following chart, the numbers highlighted in yellow are composite numbers while the numbers highlighted in blue are prime numbers. As stated above, 1 is neither prime nor composite.

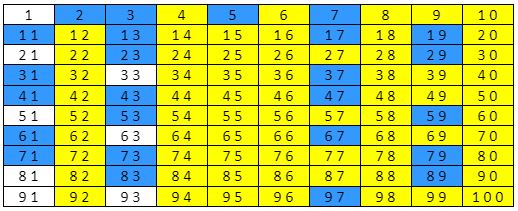
How do we differentiate between prime numbers and composite numbers? Let us find out.

Composite Numbers and Prime numbers 

The following are the differences between the composite numbers and prime numbers – 

Composite Numbers	Prime Numbers
A number that has more than two factors is called a composite number	A number having only two factors is called a prime number
Composite numbers can be both odd and even, with the only condition being that they have more than 2 factors.	Prime numbers are all odd numbers with the only exception being 2 which is an even number
The smallest composite natural number is 4	The smallest natural prime number is 2
Examples of composite numbers are 4, 6, 8 and 9	Examples of Prime Numbers are 2, 3, 5 and 7

Types of Composite Numbers

Composite Numbers can further be divided into two types – 

1. Odd Composite Numbers
2. Even Composite Numbers

Odd composite numbers are numbers that are not divisible by 2, and always leave a remainder 1 when divided by 0. For instance, in the example above, 1 , 3 , 5 , 7 and 9 are odd numbers.

Even composite numbers are numbers that are divisible by 2, leaving a remainder 0. For instance, in the example above, 2 , 4 , 6 , 8  and 10 are even numbers.

Properties of Composite Numbers

Composite Numbers have the following properties – 

1. Composite Numbers have more than 2 factors. For example, if we consider the number 12, its factors are 1, 2, 3, 4, 6 and 12. Clearly it has more than f factors. Similarly, the factors of the composite number 8 are 1, 2, 4 and 8 which is again more than 2 factors.
2. Each composite number is a factor of itself. This is because each composite number can be written as a product of 1 and the number itself. For instance, we can write 14 as 14 x 1. Similarly, 18 can be written as 18 x 1 = 18  
3. Composite numbers are evenly divisible by their factors. For instance, 6 can be written as 2 x 3 or 6 x 1.
4. The smallest composite number is 4. This is because the first counting number 1 is neither prime nor composite. The next counting numbers 2 and 3 are prime numbers. That leaves us with the number 4 which is the first composite number.
5. There is no largest composite number. This means that there is always a larger composite number than another composite number.
6. Each composite number has at least one prime number as a factor. For example, the factors of 6 are 1, 2, 3 and 6 out of which 2 and 3 are prime numbers.
7. When we add or subtract two even composite numbers, the result is always an even composite number. For example, when we add 8 and 6 we will get 8 + 6 = 14 which is an even composite number. Similarly, when we subtract 24 from 36, we will get 36 – 24 = 12. 
8. When we add an even composite number and an odd composite number, the result is always an odd composite number. For example, if we add 3, which is an odd composite number and 6 which is an even composite number, we will get, 3 + 6 = 9 which is an odd composite number. Similarly, if we add 9 which is an odd composite number and 16 which is an even composite number we will get 9 + 16 = 25 which is an odd composite number. 
9. When we multiply two even composite numbers, the result is always an even composite number. For example, if we multiply 6 which is an even composite number by 12 which is again an even composite number, the result will be 6 x 12 = 78 which is again an even composite number. Similarly, if we multiply 4 which is an even composite number by 8 which is again an even composite number, the result will be 4 x 8 = 32 which is again an even composite number.
10. When we add or subtract two odd composite numbers, the result is always an even composite number. For example, when we add 7 and 15 we will get 7 + 15 = 22. Similarly, when we subtract 21 from 37, we will get 37 – 21 = 16 which is an even composite number.
11. When we multiply two odd composite numbers, the result is always an odd composite number. For example, if we multiply 3 which is an odd composite number by 5 which is again an odd composite number, the result will be 3 x 5 = 15 which is again an odd composite number. Similarly, if we multiply 7 which is an odd composite number by 9 which is again an odd composite number, the result will be 7 x 9 = 63 which is again an odd composite number.
12. When we multiply an even composite number and an odd composite number, the result is always an even composite number. For example, if we multiply 3 which is an odd composite number by 6 which is an even composite number, the result will be 3 x 6 = 18 which is an even composite number. Similarly, if we multiply 9 which is an odd composite number by 4 which is an even composite number, the result will be 9 x 4 = 36 which is an even composite number.

Prime Factorisation of Composite Numbers

We have seen that there are more than 2 factors of every composite number. For instance, the factors of 6 are 1 ,2 , 3 and 6. This means that 6 can be written as  – 

6 = 2 x 3 or

6 = 6 x 1

From above we can see that there are different ways to represent the factorisation of a composite number. One such manner in which a composite number can be factorised is by means of representing it as a product of prime numbers. Let us check the factorisation of composite numbers up to 50 and see whether they can be represented a product of prime numbers.

Composite Number	Prime Factorisation
4	2 x 2
6	2 x 3
8	2 x 2 x 2
9	3 x 3
1 0	2 x 5
1 2	2 x 3 x 2
1 4	2 x 7
1 5	3 x 5
1 6	2 x 2 x 2 x 2
1 8	2 x 3 x 3
2 0	2 x 5 x 2
2 1	3 x 7
2 2	2 x 11
2 4	2 x 3 x 2 x 2
2 5	5 x 5
2 6	13 x 2
2 7	3 x 3 x 3
2 8	2 x 7 x 2
3 0	2 x 3 x 5
3 2	2 x 2 x 2 x 2 x 2
3 3	3 x 11
3 4	2 x 17
3 5	5 x 7
3 6	2 x 3 x 3 x 2
3 8	19 x 2
3 9	13 x 3
4 0	2 x 2 x 2 x 5
4 2	2 x 3 x 7
4 4	2 x 2 x 11
4 5	3 x 5 x 3
4 6	2 x 23
4 8	2 x 2 x 2 x 2 x 3
4 9	7 x 7
5 0	5 x 5 x 2

Key Facts and Summary

1. Composite numbers are numbers with more than two factors.
2. The numbers that have only two factors, i.e. 1 and the number itself are called prime numbers.
3. Composite Numbers have more than 2 factors.
4. Each composite number is a factor of itself.
5. Composite numbers are evenly divisible by their factors.
6. The smallest composite number is 4.
7. There is no largest composite number. This means that there is always a larger composite number than another composite number.
8. Each composite number has at least one prime number as a factor. For example, the factors of 6 are 1, 2, 3 and 6 out of which 2 and 3 are prime numbers.
9. Odd composite numbers are numbers that are not divisible by 2, and always leave a remainder 1 when divided by 0.
10. Even composite numbers are numbers that are divisible by 2, leaving a remainder 0.
11. When we add or subtract two even composite numbers, the result is always an even composite number.
12. When we add an even composite number and an odd composite number, the result is always an odd composite number. 
13. When we multiply two even composite numbers, the result is always an even composite number. 
14. When we add or subtract two odd composite numbers, the result is always an even composite number. 
15. When we multiply two odd composite numbers, the result is always an odd composite number. 
16. When we multiply an even composite number and an odd composite number, the result is always an even composite number.

Recommended Worksheets

Composite Numbers (Christmas Day Themed) Math Worksheets
Prime and Composite Numbers (Halloween Themed) Worksheets
Prime and Composite Numbers 4th Grade Math Worksheets