Introduction
Fractions are fundamental concepts in mathematics that students encounter early in their education. Decomposing fractions is an essential skill that helps students break down and simplify complex problems, making them more manageable. This article will comprehensively overview decomposing fractions, including grade appropriateness, applicable math domains and common core standards, key concepts, and examples with solutions. We will also discuss real-life applications and provide practice tests to solidify understanding.
Grade Appropriateness
Decomposing fractions is typically introduced in 4th grade and remains relevant throughout middle and high school as students study more advanced math concepts.
Math Domain
Decomposing fractions fall under the Number and Operations-Fractions domain in mathematics.
Applicable Common Core Standards
Decomposing fractions is aligned with the following Common Core Standards:
4.NF.B.3: Understand a fraction a/b with a > 1 as a sum of fractions 1/b.
5.NF.A.1: Add and subtract fractions with unlike denominators by replacing given fractions with equivalent fractions.
Definition of the Topic
Decomposing fractions refers to breaking down a fraction into a sum of simpler fractions. The goal is to express the original fraction in an equivalent form that makes computation or conceptual understanding easier.
Key Concepts
Equivalent fractions: Fractions with different numerators and denominators but represent the same value.
Simplifying fractions: The process of reducing a fraction is by taking its numerator and denominator and dividing them by their greatest common factor.
Least Common Denominator (LCD): The smallest multiple that two or more denominators share, used to find equivalent fractions with common denominators.
Discussion with Illustrative Examples
Decompose means ‘breaking apart’, ‘splitting up’, or ‘dividing into smaller parts’. Decomposing a fraction into smaller fractions adds all the smaller parts together, resulting in the initial fraction.
Decomposing Fractions into Unit Fractions
A unit fraction is a fraction with one as a numerator. For example, $\frac{1}{3}$,$\frac{1}{5}$,$\frac{1}{7}$,$\frac{1}{9}$, etc.
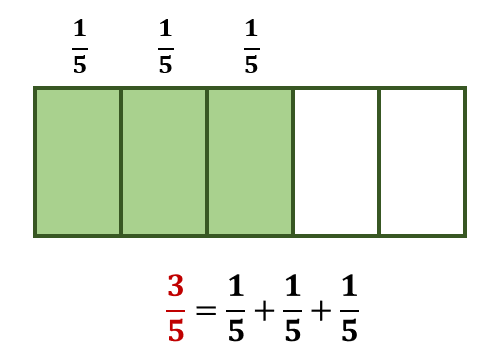
When we break a fraction into unit fractions, we split it into equal parts. Let us say, for example, $\frac{3}{5}$=$\frac{1}{5}$+$\frac{1}{5}$+$\frac{1}{5}$, which is the same as three times the unit fraction $\frac{1}{5}$.
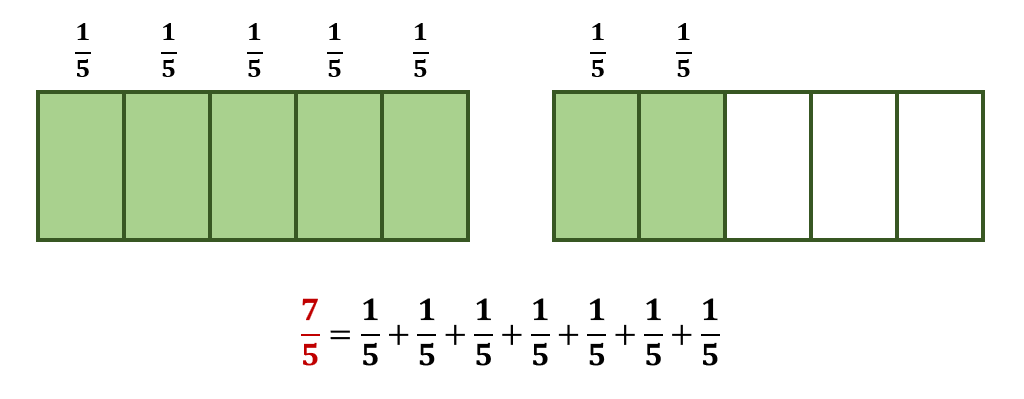
Let us consider another fraction, say $\frac{7}{5}$; we can decompose it into a sum of unit fractions, as shown below.
Decomposing Fractions into Different Denominators
This method decomposes a fraction into smaller fractions with different denominators. We express the fraction as the sum of fractions which are not all unit fractions.
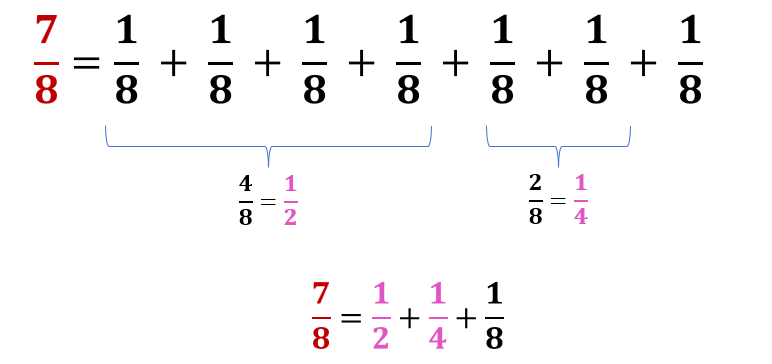
Let us consider the fraction $\frac{7}{7}$ and decompose it into the sum of three fractions with different denominators. As shown below, by getting the sum of unit fractions, we can simplify fractions and obtain $\frac{7}{8}$=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$.
Examples with Solution
Example 1
Decompose $\frac{5}{6}$ into a sum of unit fractions (fractions with a numerator of 1).
Solution
To decompose $\frac{5}{6}$ into a sum of unit fractions, we must have the sum of five one-sixths.
$\frac{5}{6}$ =$\frac{1}{6}$ +$\frac{1}{6}$ +$\frac{1}{6}$ +$\frac{1}{6}$ +$\frac{1}{6}$
Example 2
Decompose $\frac{9}{11}$ as the sum of three equal fractions.
Solution
If we split the number into three equal parts, we have 9=3+3+3. Therefore,
$\frac{9}{11}$=$\frac{3}{11}$+$\frac{3}{11}$+$\frac{3}{11}$
Example 3
Using two smaller fractions with different denominators, decompose $\frac{8}{15}$.
Solution
Since we must obtain two smaller fractions with different denominators, we have,
$\frac{1}{15}$+$\frac{1}{15}$+$\frac{1}{15}$=$\frac{3}{15}$=$\frac{1}{15}$ and
$\frac{1}{15}$+$\frac{1}{15}$+$\frac{1}{15}$+$\frac{1}{15}$+$\frac{1}{15}$=$\frac{1}{15}$=$\frac{1}{3}$.
Therefore, $\frac{8}{15}$=$\frac{1}{5}$+$\frac{1}{3}$.
Real-life Application with Solution
Problem 1
Imagine that you and two friends want to share $\frac{6}{7}$ of a pizza equally. You can decompose the fraction into three equal parts to determine how much pizza each person will receive.
Solution
$\frac{6}{7}$÷3=($\frac{1}{7}$+$\frac{1}{7}$+$\frac{1}{7}$+$\frac{1}{7}$+$\frac{1}{7}$)÷3
=($\frac{1}{7}$+$\frac{1}{7}$)+($\frac{1}{7}$+$\frac{1}{7}$)+($\frac{1}{7}$+$\frac{1}{7}$)
=$\frac{2}{7}$+$\frac{2}{7}$+$\frac{2}{7}$
Each person will receive $\frac{2}{7}$ of the pizza.
Problem 2
Maria, Martin, and Mario ate $\frac{3}{8}$ of the pie. Write an equation to show how much of the pie each ate.
Solution
Dividing the numerator into three equal parts, we have 3=1+1+1. So,
$\frac{3}{8}$=$\frac{1}{8}$+$\frac{1}{8}$+$\frac{1}{8}$
Hence, each of them ate $\frac{1}{8}$ of the pie.
Practice Test
1. Decompose $\frac{3}{4}$ into a sum of unit fractions.
2. Decompose $\frac{2}{7}$ into a sum of smaller fractions with the same denominators.
3. Decompose $\frac{11}{12}$ into a sum of unit fractions.
4. Decompose $\frac{9}{24}$ into a sum of three smaller fractions with different denominators.
5. Decompose $\frac{6}{8}$ into a sum of unit fractions.
6. Decompose $\frac{13}{15}$ into a sum of unit fractions.
Answers:
1. $\frac{3}{4}$ =$\frac{1}{4}$ +$\frac{1}{4}$ +$\frac{1}{4}$
2. $\frac{6}{7}$=$\frac{2}{7}$ +$\frac{2}{7}$ +$\frac{2}{7}$
3. $\frac{11}{12}$ =$\frac{1}{12}$ +$\frac{1}{12}$ +$\frac{1}{12}$ +$\frac{1}{12}$ +$\frac{1}{12}$ +$\frac{1}{12}$ +$\frac{1}{12}$ +$\frac{1}{12}$ +$\frac{1}{12}$ +$\frac{1}{12}$ +$\frac{1}{12}$
4. $\frac{9}{24}$ =$\frac{1}{12}$ +$\frac{1}{8}$ +$\frac{1}{6}$
5. $\frac{6}{8}$ =$\frac{1}{8}$ +$\frac{1}{8}$ +$\frac{1}{8}$ +$\frac{1}{8}$ +$\frac{1}{8}$ +$\frac{1}{8}$
6. $\frac{13}{15}$ =$\frac{1}{15}$ +$\frac{1}{15}$ +$\frac{1}{15}$ +$\frac{1}{15}$ +$\frac{1}{15}$ +$\frac{1}{15}$ +$\frac{1}{15}$ +$\frac{1}{15}$ +$\frac{1}{15}$ +$\frac{1}{15}$ +$\frac{1}{15}$ +$\frac{1}{15}$ +$\frac{1}{15}$
Frequently Asked Questions (FAQs)
What is the purpose of decomposing fractions?
Decomposing fractions helps students understand the concept of fractions, simplifies complex problems and makes computation easier.
Can all fractions be decomposed into unit fractions?
Yes, all fractions can be decomposed into a sum of unit fractions.
Can you decompose fractions with unlike denominators?
Yes, you can decompose fractions with unlike denominators by finding a common denominator or by using a combination of different denominators.
Why is decomposing fractions important in math?
Decomposing fractions is important because it helps students develop a strong foundation in understanding fractions, which is crucial for more advanced math concepts. It also makes solving problems involving fractions easier by breaking them down into simpler components.
How can decomposing fractions help with the addition and subtraction of fractions?
Decomposing fractions can help students find equivalent fractions with common denominators, which is necessary for adding and subtracting fractions with unlike denominators.
Recommended Worksheets
Decomposing Fractions (Gardening Themed) Math Worksheets
Decomposing Money (World Animals Day Themed) Math Worksheets
Decomposing Numbers within 20 1st Grade Math Worksheets









