Introduction
Equal groups enable a visual representation of solving problems that involve multiplication. If a group contains the same number of items as all the other groups, it is considered to be equal. The multiplication sign, ×, denotes multiplication, which signifies “equal groupings of.”
To describe the equal group models, it is important to count the number of groups shown and the number of items or objects in each group. This article will discuss the definition of equal groups, how to illustrate equal groups and show multiplication using equal groups.
What are equal groups?
Definition
The act of arranging various things or numbers in groups in the same quantities is known as an equal group.
If a group contains the same number of items as all the other groups, it is considered to be equal. The multiplication sign, ×, denotes multiplication, which signifies “equal groupings of.”
For example, 3 × 3 can be read as 3 equal groups of 3.
For another example, 5 × 5 can be read as 5 equal groups of 5.
The number of equal groups multiplied by the number of objects in each group forms the total.
Let us say we have 20 objects, and we will group these objects that form the number 20.
We have 1 group of 20, so we have 1 × 20 = 20.
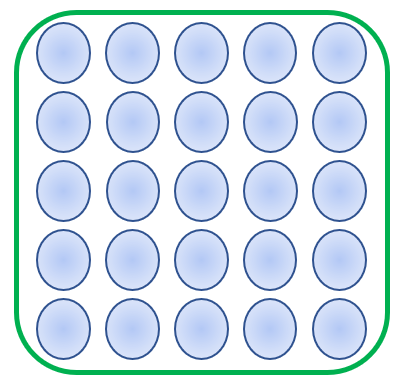
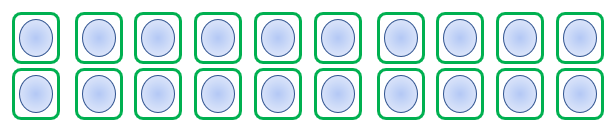
We have 20 equal groups of 1 object, so we have 20 × 1 = 20.
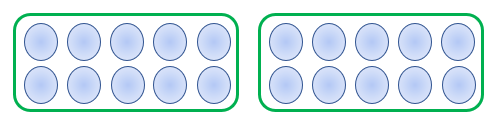
We have 2 equal groups of 10 objects, so we have 2 × 10 = 20.
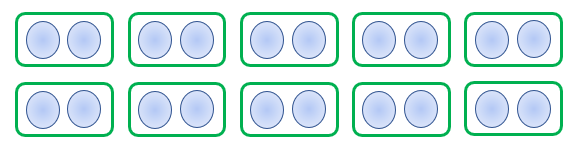
We have 10 equal groups of 2 objects, so we have 10 × 2 = 20.
We have 4 equal groups of 5 objects, so we have 4 × 5 = 20.
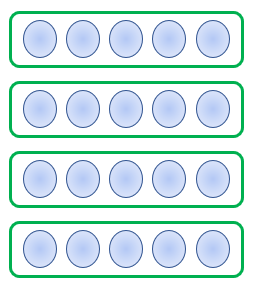
We have 5 equal groups of 4 objects, so we have 5 × 4 = 20.

The number of equal groups multiplied by the number of objects in each group forms our times multiplication tables.
Equal Groups Models
To describe the equal group models, it is important to count the number of groups shown and the number of items or objects in each group.
Let us say refer to the image below as an example.

In the given figure, there are 5 equal groups with 3 objects in each. It may be noted as 5 groups of 3. Using multiplication, this is expressed as 5 × 3 = 15.
For more examples, let us answer the following group models.
Directions: Give details about the equal group models in the blanks.
1. 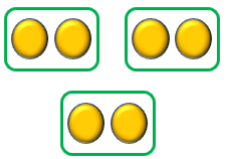 | ___ equal groups of _______ × ___ = ___ |
2.  | ___ equal groups of _______ × ___ = ___ |
3. 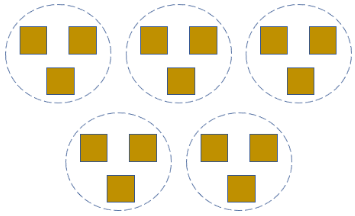 | ___ equal groups of _______ × ___ = ___ |
4. 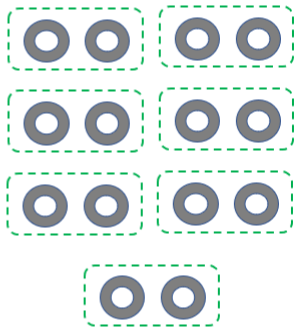 | ___ equal groups of _______ × ___ = ___ |
5. 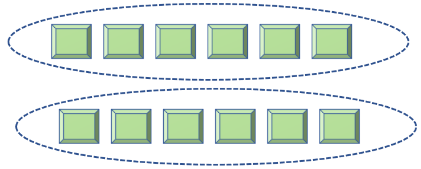 | ___ groups of _______ × ___ = ___ |
Answers:
1. 3 equal groups of 2 3 × 2 = 6
2. 4 equal groups of 6 4 × 6 = 24
3. 5 equal groups of 3 5 × 3 = 15
4. 7 equal groups of 2 7 × 2 = 14
5. 2 equal groups of 6 2 × 6 = 12
How to Count Equal Groups?
Since equal groups have the same number of items or objects in each group, we can use equal groups to find how many objects in all.
Let us say, for example, there are 3 equal groups of 4 stars. It means that there are 3 equal groups with 4 stars in each group. We can skip count by fours to find how many stars there are, so we have 4, 8, and 12.

Therefore, in 3 equal groups of 4 stars, there are 12 stars in all.
As for another example, let us have 6 equal groups of 5 squares. It means that there are 6 groups with 5 squares in each group. Using skip counting by five, we have 5, 10, 15, 20, 25, and 30.
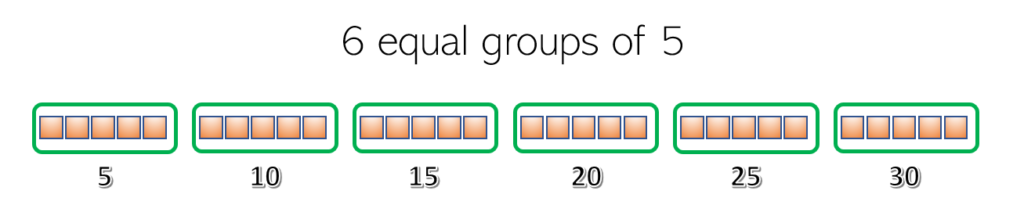
Thus, in 6 equal groups of 5 squares, there are 30 squares.
How to Count Equal Groups to Find a Total?
We can use equal groups to find how many in all. Equal groups have the same number of objects in each group. We can skip count to find how many objects in all.
Let us say, for example, 4 equal groups of 5. Since there are 4 equal groups of 5, it means that there are 4 equal groups with 5 objects in each group.
We can say there are 4 fives and skip count by five. Hence, we have 5, 10, 15, and 20. The image below shows an illustration of the given.
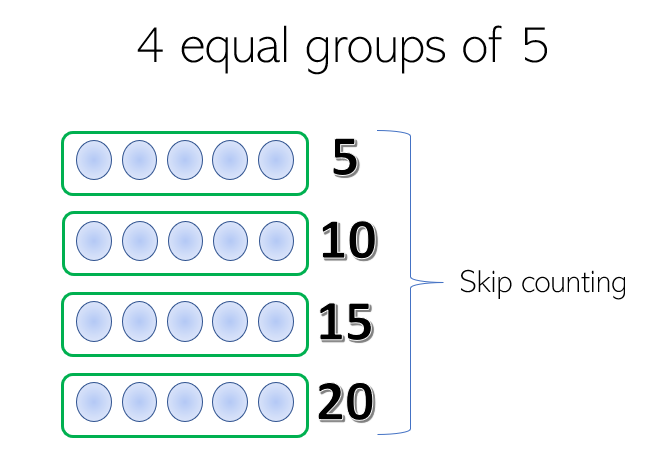
Therefore, there are 20 objects in all.
What if we had 5 equal groups of 4? Would our answer change?
In 5 groups of 4, there are 5 equal groups with 4 items in each group. We can also say that there are 5 fours. To find the total objects, we can skip count by fours.
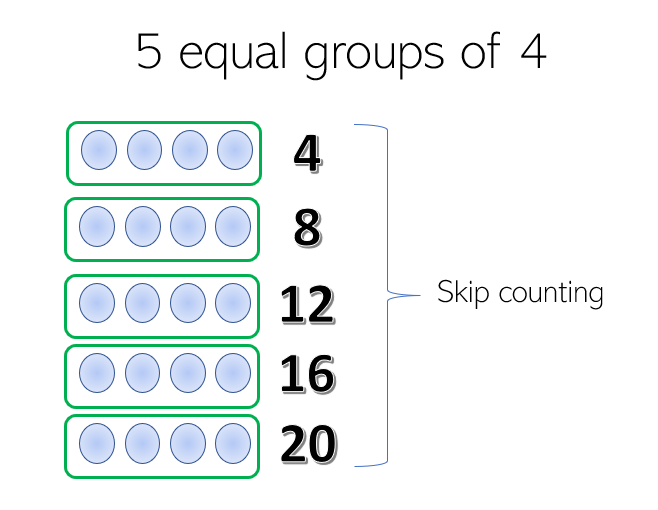
Thus, there are 20 objects in all.
The illustration below shows the comparison of 4 equal groups of 5 and 5 equal groups of 4.
4 groups of 54 × 5 = 20 | 5 groups of 45 × 4 = 20 |
| The answer stays the same. |
As for another example, let us have 3 equal groups of 6. Since there are 3 equal groups of 6, it means that there are 3 equal groups with 6 objects in each group.
We can say there are 3 sixes, and we can skip count by six. Thus, we have 6, 12, and 18. The figure below shows an illustration of the given.
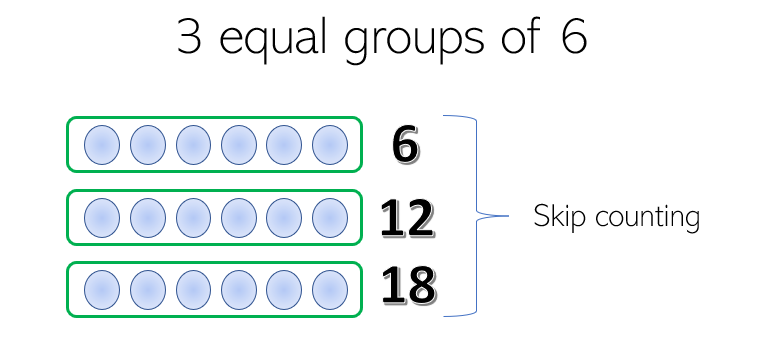
Therefore, there are 18 objects in all.
What if we had 6 groups of 3? Would our answer change?
In 6 groups of 3, there are 6 equal groups with 3 objects in each group. We can also say that there are 6 threes. To find the total objects, we can skip count by threes.
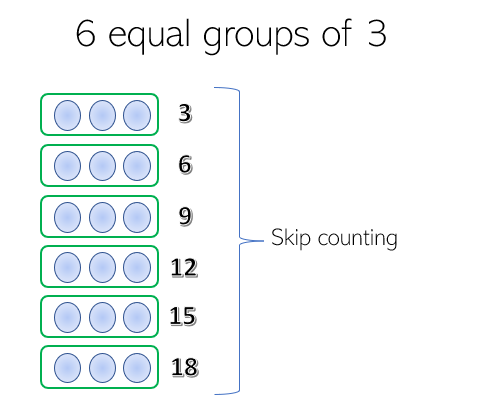
Thus, there are 18 objects in all.
The illustration below compares 3 groups of 6 and 6 groups of 3.
3 equal groups of 63 × 6 = 18 | 6 equal groups of 36 × 3 = 18 |
| The answer stays the same. |
Ways of Representing Equal Groups
There are several ways of representing equal groups: repeated addition, multiplication sentences, array, and division sentences.
Repeated Addition
Repeated addition can be used to determine the total number of objects if there are several equal groups.
Let us have the image below. There are 3 groups, each having 9 squares. If we add the number 9 three times, we can solve the total number of squares. Hence, we have 9 + 9 + 9 =27.
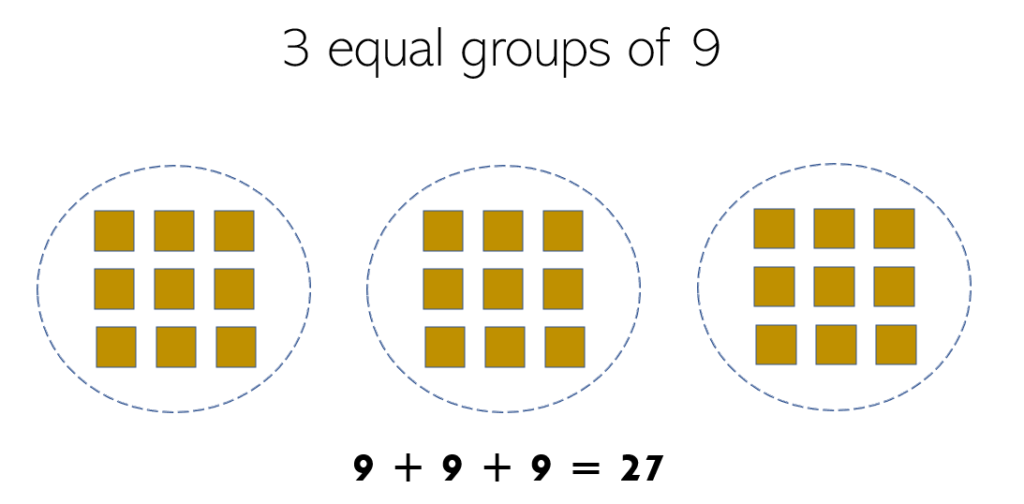
Multiplication Sentence
Equal groups can be represented as a multiplication statement, which can then be solved to give the solution.
Let us use the same groups of squares above. We have 3 equal groups of 9 squares. Using a multiplication sentence, it can be expressed as 3 × 9 = 27. Moreover, the total of 27 squares may also be expressed as 9 equal groups of 3, which is a mathematical statement is 9 × 3 = 27.
3 equal groups of 93 × 9 = 27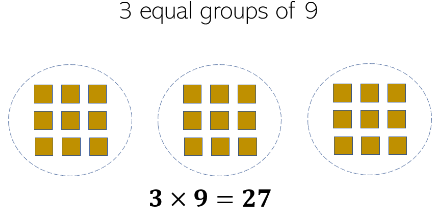 | 9 equal groups of 39 × 3 = 27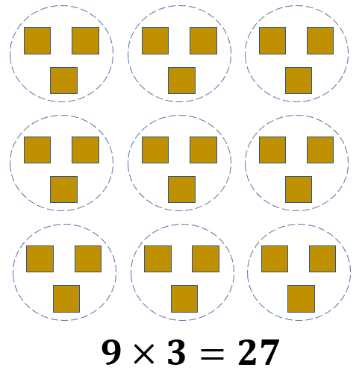 |
Arrays
Another way of representing equal groups is using arrays. Using arrays is visually organized with the use of columns and rows.
Let us say we have the same example, 3 equal groups of 9 squares. We may have 3 rows of 9 squares each or 3 columns of 9 squares each.
3 rows of 9 squares each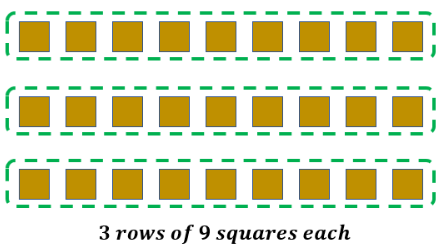 | 3 columns of 9 squares each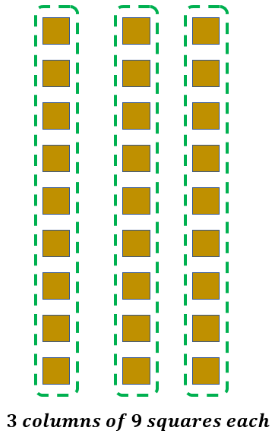 |
Division Sentence
Splitting objects into equal groups is the definition of division. We can therefore represent equal groups as a division expression. The quotient stands for either the number of groups or the number of items or objects in each group. Hence, we have,
Total number of objects ÷ Number of Equal Groups = number of objects in each group
Total number of objects ÷ number of objects in each group = Number of Equal Groups
27 squares in 3 groups of 9 squares each27 ÷ 3 = 9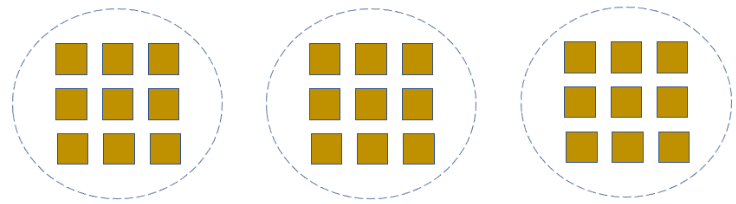 In total, there are 27 squares. There are three groups, each containing nine squares. |
27 squares in 9 groups of 3 squares each27 ÷ 9 = 3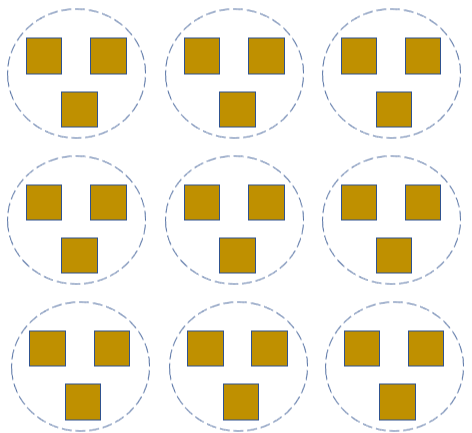 In total, there are 27 squares. There are nine groups, each containing three squares. |
Multiplication Using Equal Groups of Objects
Multiplication using equal groups of objects is a visual approach to introduce the concept of multiplication. Equal grouping is the act of arranging a variety of things, objects or numbers in groups in the same quantities.
Multiplication by grouping is used to introduce the times multiplication tables or the times tables. The idea of multiplication by grouping is to show multiplication as collecting equal groups of a specific number.
Let us use the objects below to show the idea of multiplication by grouping.

There is a total of 24 objects in the given figure. There are different ways to illustrate this as multiplication using equal groups.
We can group the total number of 24 into 4 equal portions.
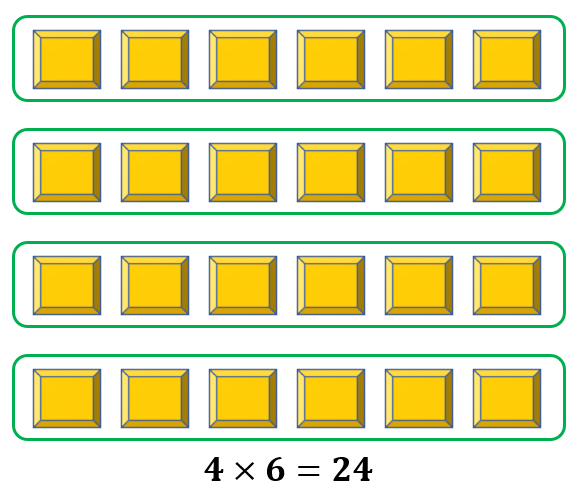
We now have 4 equal groups, with each containing 6 objects. This may also be expressed as 4 equal groups of 6. In math with a multiplication symbol, we may write this as 4 × 6 = 24.
The total number of objects, 24, may also be illustrated using 8 equal groups.

We now have 8 equal groups, with each containing 3 objects. This may also be expressed as 8 equal groups of 3. In math with a multiplication symbol, we may write this as 8 × 3 = 24.
Another way of showing a total of 24 objects using grouping is to have 2 equal portions.
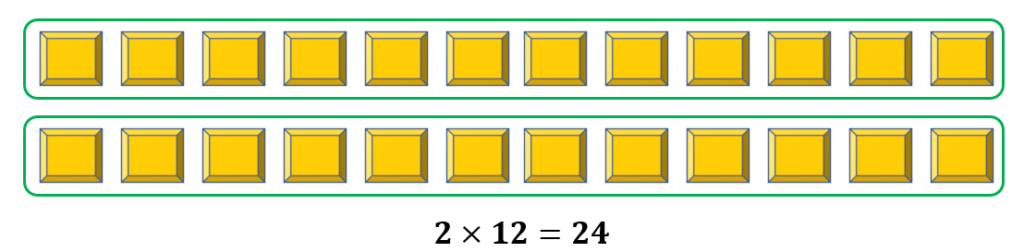
We now have 2 equal groups, with each containing 12 objects. This may also be expressed as 2 equal groups of 12. In math with a multiplication symbol, we may write this as 2 × 12 = 24.
The illustrations above are just 3 ways of multiplication using equal groups for the number 24. Moreover, it can also be expressed as 12 × 2 = 24, which means 12 equal groups of 2, 3 × 8 = 24, which means 3 equal groups of 8, and 6 × 4 = 24, which means 6 equal groups of 4.
More Examples
Example 1
Tess has 5 jars. Each jar has 3 candies. How many candies are there in all?
Solution
The image below shows the jars with 5 candies each.

There are 5 groups, with 3 candies in each group. Using groups, we can find the total number of candies by skip counting or multiplication.
If we skip count by threes, we have 3, 6, 9, 12, and 15. In math multiplication, we may express this as 5 × 3.
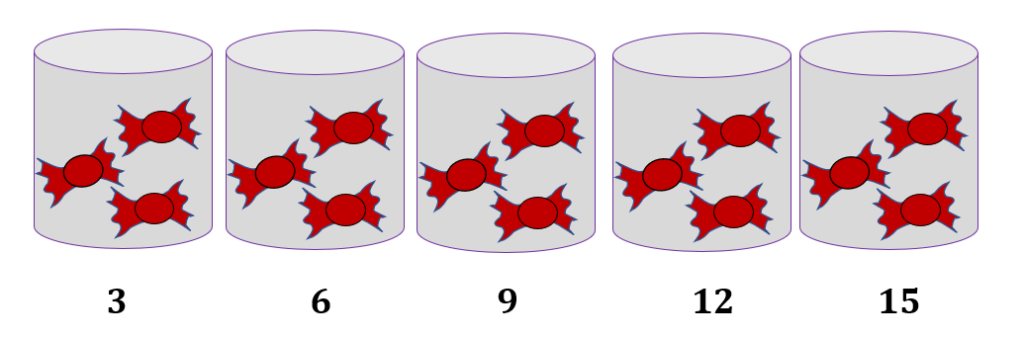
Therefore, there are 15 candies in all.
Example 2
Three girls each have 6 coins. How many coins are there altogether?
Solution
The illustration below shows the coins of each girl.

There are 3 groups, with 6 coins in each group. Using groups, we can find the total number of coins by skip counting or multiplication.
If we skip count by six, we have 6, 12, and 18. In math multiplication, we may express this as 3 × 6.
Therefore, there are 18 coins in all.
Example 3
Aunt Mary has 7 vases. If each vase has 3 flowers, how many are there?
Solution
The image below shows the vases with 3 flowers each.

There are 7 groups, with 3 flowers in each group. We can find the total number of flowers by skip counting or multiplication using groups.
If we skip count by three, we have 3, 6, 9, 12, 15, 18, and 21. In math multiplication, we may express this as 7 × 3.
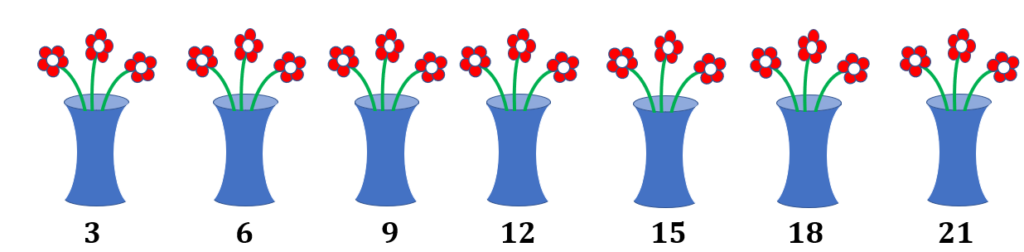
Therefore, there are 21 flowers in all.
Summary
The act of arranging various things or numbers in groups in the same quantities is known as an equal group.
If a group contains the same number of items as all the other groups, it is considered to be equal. The multiplication sign, ×, denotes multiplication, which signifies “equal groupings of.”
To describe the equal group models, it is important to count the number of groups shown and the number of items or objects in each group. Let us say, for example, there are 5 groups with 3 objects in each. This may be noted as 5 groups of 3. Using multiplication, this is expressed 5 × 3 = 15.
Multiplication using equal groups of objects is a visual approach to introduce the concept of multiplication. Equal grouping is the act of arranging a variety of things, objects or numbers in groups in the same quantities.
Multiplication by grouping is used to introduce the times multiplication tables or the times tables. The idea of multiplication by grouping is to show multiplication as collecting equal groups of a specific number.
Ways of Representing Equal Groups
There are several ways of representing equal groups, and these are
( a ) Repeated addition
( b ) Multiplication Sentences
( c ) Array
( d ) Division Sentences.
Frequently Asked Questions on Multiplication as Equal Groups
Why are equal groups important in multiplication?
A visual method of teaching multiplication is using equal groups of objects. The act of grouping different items, objects, or numbers in equal groupings is known as an equal grouping.
The times tables or times multiplication tables are introduced using multiplication by grouping. The concept behind multiplication by grouping is to represent multiplication as the collection of an exact number of equal groups.
The images below show that 4 × 5, 5 × 4, 1 × 20, 20 × 1, 10 × 2, and 2 × 10 have the same answer.
We have 1 group of 20, so we have 1 × 20 = 20. | We have 20 equal groups of 1 object, so we have 20 × 1 = 20. |
We have 2 equal groups of 10 objects, so we have 2 × 10 = 20. | We have 10 equal groups of 2 objects, so we have 10 × 2 = 20. |
We have 4 equal groups of 5 objects, so we have 4 × 5 = 20. | We have 5 equal groups of 4 objects, so we have 5 × 4 = 20. |
What is an equal group in a problem?
Equal groups are those that include the same number of objects. As a result, the number of items or objects in each group is equal.
Let us say, for example, that each jar will have the same number of chocolates; for instance, if there are 5 jars and 3 chocolates are placed in each one. Here, we state that there are 5 equal groups of 3, which means that each box contains 3 chocolates.
Equal groups are frequently used in problems that involve multiplication and skip counting.
What is an example of equal groups in math?
Equal grouping is the act of arranging a variety of things, objects, or numbers in groups in the same quantities. Equal groups are frequently used in problems that involve multiplication and skip counting.
Let us say, for example, 4 equal groups of 5. Since there are 4 equal groups of 5, it means that there are 4 equal groups with 5 objects in each group.
We can say there are 4 fives and skip count by five. Hence, we have 5, 10, 15, and 20. The image below shows an illustration of the given.
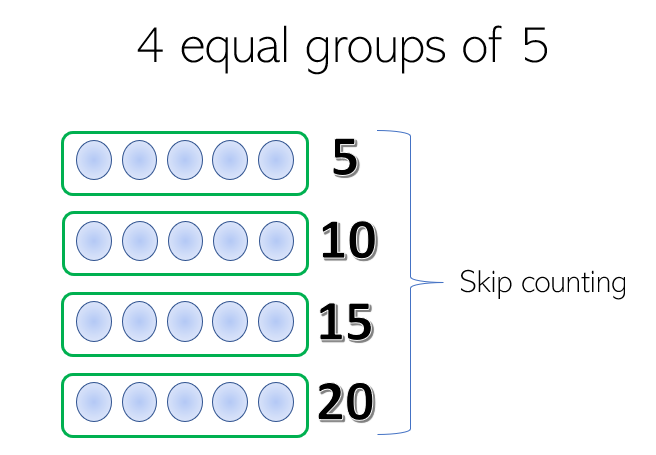
Therefore, there are 20 objects in all.
What if we had 5 groups of 4? Would our answer change?
In 5 groups of 4, there are 5 equal groups with 4 items in each group. We can also say that there are 5 fours. To find the total objects, we can skip count by fours.

Thus, there are 20 objects in all.
How to teach students multiplication as equal groups?
Multiplication using equal groups of objects is a visual approach to introduce the concept of multiplication. Equal grouping is the act of arranging a variety of things, objects, or numbers in groups in the same quantities.
Multiplication by grouping is used to introduce the times multiplication tables or the times tables. The idea of multiplication by grouping is to show multiplication as collecting equal groups of a specific number.
Let us use the objects below to show the idea of multiplication by grouping.

There is a total of 12 objects in the given figure. There are different ways to illustrate this as multiplication using equal groups.
We can group the total number 12 into 4 equal portions.

We now have 4 equal groups, with each containing 3 objects. This may also be expressed as 4 equal groups of 3. In math with a multiplication symbol, we may write this as 4 × 3 = 12.
The total number of objects, 12, may also be illustrated using 6 equal groups.
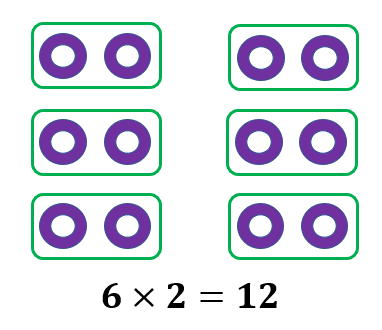
We now have 6 equal groups, with each containing 2 objects. This may also be expressed as 6 equal groups of 2. In math with a multiplication symbol, we may write this as 6 × 2 = 12.
Another way of showing a total of 12 objects using grouping is to have 3 equal portions.
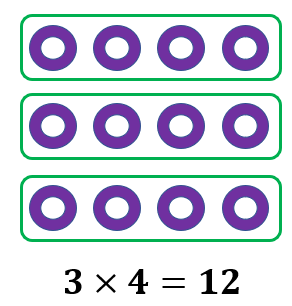
We now have 3 equal groups, with each containing 4 objects. This may also be expressed as 3 equal groups of 4. In math with a multiplication symbol, we may write this as 3 × 4 = 12.
The illustrations above are just 3 ways of multiplication using equal groups for the number 12. Moreover, it can also be expressed as 1 × 12 = 12, which means 1 equal group of 12; 2 × 6 = 12, which means 2 equal groups of 6; and 12 × 1 = 12, which means 12 equal groups of 1.
What are the ways to represent equal groups?
There are several ways of representing equal groups: repeated addition, multiplication sentences, array, and division sentences.
Recommended Worksheets
Multiplication Property (Valentine’s Day Themed) Math Worksheets
Multiplication Tables (St. Patrick’s Day Themed) Math Worksheets
Fact Families for Multiplication and Division (Summer Themed) Math Worksheets









