Laws of Integral Exponent

Introduction

Exponents are a fundamental aspect of mathematics that every student will encounter. They are one of the keys to unlocking more complex mathematical ideas and operations. This article will concentrate on specific rules that make dealing with exponents easier and simpler.

Grade Appropriateness

This topic is typically introduced around 6th grade in most educational curricula and further reinforced and deeply understood in 7th and 8th grades. However, the understanding and application of these laws carry on throughout high school and beyond.

Math Domain

The laws of integer exponents fall under Number Theory and Algebra.

Applicable Common Core Standards

The Common Core Standards related to this topic are:

CCSS.MATH.CONTENT.6.EE.A.1: Write and evaluate numerical expressions involving whole-number exponents.

CCSS.MATH.CONTENT.8.EE.A.1: Know and apply the properties of integer exponents to generate equivalent numerical expressions.

Definition of the Topic

An exponent is a number that indicates the number of times a base number is multiplied by itself. If n is a positive integer, then an is the product of multiplying ‘a’ by itself ‘n’ times. 

The laws of integral exponents govern the manipulation of expressions involving exponents.

Key Concepts

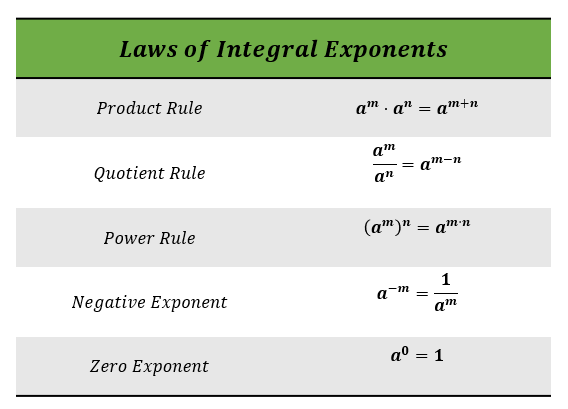
For any nonzero term a where m and n are real numbers, the laws of integer exponents include the following:

Product of Powers Rule  When multiplying like bases, you can add the exponents: am⋅ an = am+n.	Quotient of Powers Rule When dividing like bases, you can subtract the exponents: $\frac{a^m}{a^n}$ = am-n.
Power of a Power Rule  When raising a power to a power, you can multiply the exponents: (am)n = am⋅n.	Zero Exponent Rule Any nonzero number raised to the power of zero is 1: a0= 1.
Negative Exponent Rule A nonzero number raised to a negative exponent is the reciprocal of the number raised to the opposite positive exponent: a-n =$\frac{1}{a^n}$.

Discussion with Illustrative Examples

Exponents

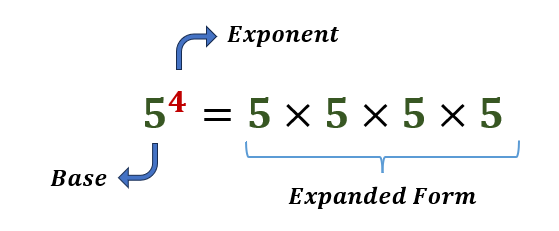
Exponents are used to show the repeated multiplication of a number by itself.

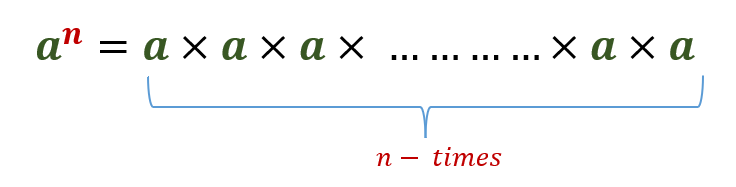
Say, for example, 5×5×5×5 can be expressed as 5⁴. The exponent is 4, meaning the number of times the base number 5 is multiplied.  

Laws of Integral Exponents

The Laws of Integral Exponents are fundamental math concepts that guide in evaluating complex expressions, especially those involving exponents. These laws include the following:

Product Rule

Copy the base and add the exponents when multiplying expressions with the same base but different exponents.

a^m.aⁿ=a^m+n

Examples

1. b³.b⁵=(b⋅b⋅b)(b⋅b⋅b⋅b⋅b)=b⁸

    Simplifying this expression using the product rule, we have,

     b³.b⁵=b³⁺⁵=b⁸ 

2. (c²d4)(cd³)=(c²⁺¹)(d⁴⁺³)=c³d⁷

Quotient Rule

Copy the base and subtract the exponents when dividing expressions with the same base.

$\frac{a^m}{a^n}$=a^m-n

Examples

1. $\frac{b^6}{b^4}$=$\frac{b⋅b⋅b⋅b⋅b⋅b}{b⋅b⋅b⋅b}$

    When we simplify this expression using the quotient rule, we will have,

    $\frac{b^6}{b^4}$=b^6-4=b² 

2. $\frac{c^9d^5}{c^3d^2}$=c^9-3d^5-4=c⁶d³ 

Power Rule

When an expression with an exponent is raised to another integer, multiply these exponents.

(a^m)ⁿ=a^m⋅n

Examples

1. (b⁴)³=b⁴.b⁴.b⁴=(b⁴.b⁴.b⁴.b⁴)(b⁴.b⁴.b⁴.b⁴)(b⁴.b⁴.b⁴.b⁴)=b¹²

     Simplifying the expression applying the power rule, we get,

     (b⁴)³=b^4×3=b¹²

2. (3c²d⁴)³=(3)³(c²)³(d⁴)³=3³c^2×3d^4×3=27c⁶d¹²

Negative Exponent

When the expression is raised to a negative integer, we get the reciprocal of the base number.

a^-m=$\frac{1}{a^m}$

Examples

1. b^-6=$\frac{1}{b^6}$

2. $\frac{c^{-5}}{d^{-3}}$=$\frac{d^3}{c^5}$

Zero Exponent

Any expression raised to zero is equal to 1.

a⁰=1

Examples

1. b⁰=1

2. 10⁰=1

3. (c²d⁴)⁰=1

Examples with Solutions

Example 1

Simplify the following expressions by applying the appropriate law/s of exponents.

i. (2x³y²)⁴

ii.$\frac{4a^5b^6}{8a^2b^3}$

iii. (2a²+3b²-c)⁰

Solution

i. (2x³y²)⁴=(2)⁴ (x³)⁴(y²)⁴=2⁴x^3⋅4y^2⋅4=16x¹²y⁸  (Power Rule and Product Rule)

ii. $\frac{4a^5b^6}{8a^2b^3}$=$\frac{1}{2}$a^5-2b^6-3=$\frac{1}{2}$a³b³ (Quotient Rule)

iii. (2a²+3b²-c)⁰=0 (Zero Exponent Rule)

Example 2

Simplify the following expressions.

i. 3^-5

ii.$\frac{a^{-4}b^{-5}c^{-1}}{a^2b^2c^2}^2$

Solution

i. 3^-5=$\frac{1}{3^5}$=$\frac{1}{243}$

ii.($\frac{a^{-4}b^{-5}c^{-1}}{a^2b^2c^2}$)²=(a^-4-2)(b^-5-2)(c^-1-2)=a^-6b^-7c^-3=$\frac{1}{a^6b^7c^3}$

Real-life Application with Solution

Problem 

Find the area of a rectangle whose length measures 4a²b³ and width of 2a³b⁴.

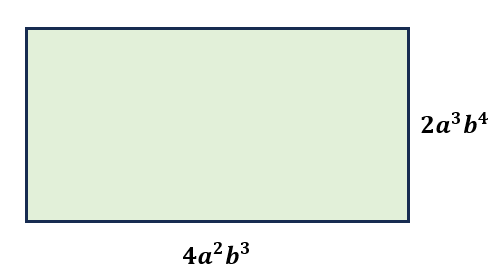
Solution

Since the area of a rectangle is calculated using the formula AreaRectangle=Length×Width, when we substitute the given measurements, we get,

Area=4a²b³ x 2a³b⁴

Applying the product rule of exponents, we have,

Area=(4⋅2)(a²⁺³)(b³⁺⁴)

Area=8a⁵b⁷

Hence, the area of the rectangle is 8a5b7.

Practice Test

Simplify each expression.

a. 2⁴.2³

b. $\frac{5^6}{5^2}$

c.  (3²)³

d. 7⁰a⁴

e. $\frac{3^5a^{-2}b^5}{b^4}$

Answers:

a. 2⁴.2³=2⁴⁺³=2⁷=128

b. $\frac{5^6}{5^2}$=5⁴=625

c.  (3²)³=3^2×3=3⁶=729

d. 7⁰a⁴=(1)a⁴ = a⁴

e. $\frac{3^5a^{-2}b^5}{b^4}$ = $\frac{243b}{a^2}$

Frequently Asked Questions (FAQs)

Why does any number to the power of zero equal one? 

According to the laws of exponents, when we divide any number by itself, we get 1. 

For example, $\frac{2^3}{2^3}$ equals 1. 

According to the quotient of powers rule, we can also express this as 2^3-3, which is 2⁰. Therefore, any number to the power of zero is 1.

Can zero be raised to an exponent? 

Zero can be raised to a positive exponent, and the result will always be zero. However, zero to the power of zero (0⁰) is an indeterminate form, which means it does not have a clear, universally accepted value.

What does a negative exponent mean? 

A negative exponent means that the base is on the wrong side of the fraction line, so you flip the base to the other side. For example, 2^-3 equals $\frac{1}{2^3}$ or $\frac{1}{8}$.

Why do we add exponents when multiplying like bases? 

When you multiply like bases, you add more base multiplication. The exponent indicates how many times a number is multiplied by itself, so when you multiply like bases, you add to the number of times the base is being multiplied, which is why the exponents are added.

What happens if I raise a power to another power? 

When you raise a power to another power, you multiply the exponents. This is because you increase the number of times you multiply the base by itself.

Recommended Worksheets

Laws of Integral Exponent (Labor Day Themed) Math Worksheets
Exponents (Museum Themed) Worksheets
Exponential Growth and Decay (Financial Risk Management Themed) Math Worksheets